Critérios de divisibilidade de cada número: resumo e simulado
É muito comum perder um tempão fazendo pequenos cálculos para resolver questões de Matemática, especialmente quando envolve divisão! Então, se liga nessa aula de Matemática Básica sobre os critérios de divisibilidade para otimizar seu tempo no Enem!
Uma das dificuldades que pega a gente em um vestibular é o tempo que a gente perde fazendo uma divisão. Ensinaram para a gente umas regrinhas para acelerar o processo, porém éramos crianças e acabamos esquecendo.
Para te ajudar a relembrar as técnicas básicas da divisão e acelerar seus cálculos no Enem, preparamos esta aula de Matemática Básica. Aprenda essas regras ou critérios de divisibilidade com a gente no Curso Enem Gratuito.
Você sabe dividir? No nosso dia dividimos muitas coisas não é mesmo? Um chocolate com uma amiga ou amigo, uma pizza com os amigos e até dividimos a conta ao almoçar com alguém. Mas quando pega de dividirmos valores grandes ou pequenos demais sem a calculadora, às vezes, bate um pânico!!!
Mas, não se preocupe! Nesta aula vamos estudar os conceitos de divisibilidade, regras que são denominadas critérios de divisibilidade.
Assim, você não terá mais aquela dúvida quando tiver que fazer divisões exatas e não exatas para resolver questões de matemática (ou quanto você vai pagar da conta) e vai saber rapidamente se um número é ou não divisível por outro. Também vamos apresentar algumas noções sobre múltiplos e divisores.

No ensino fundamental aprendemos que uma divisão exata é aquela que o resto é igual a zero. Enquanto a divisão não exata possui o resto diferente de zero e menor que divisor (número que está dentro da chave de divisão).
Resumo sobre critérios de divisibilidade
Confira agora com o professor Lucas Borguesan, do canal do Curso Enem Gratuito, uma introdução ao tema da Divisibilidade:
Domine o que é Dividendo, Divisor, Quociente, e Resto
Veja o exemplo abaixo uma divisão e o nomes de cada termo:
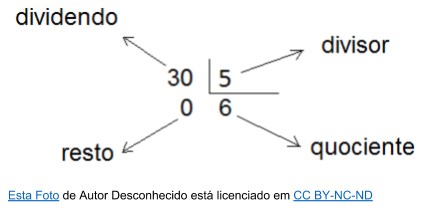
Neste exemplo, podemos afirmar que o divisor de 30 é 5 e que 30 dividido por 5 é uma divisão exata.
Dessa afirmação podemos tirar dois conceitos:
a) Se 30 é dividido por 5 é igual a 6 então 30 é múltiplo de 6 pois 6 X 5 = 30.
b) 30 é divisível por 6 e 5, pois ambas divisões são exatas
A partir desse raciocínio podemos concluir que:

Resumo básico sobre Divisão:
Existem algumas regras para que facilitem nossa vida ao realizarmos uma divisão com números naturais que são denominadas de critérios de divisibilidade.
Veja os Critérios de Divisibilidade
Vamos a eles:
1) Critério de divisibilidade por 2:
Podemos dividir um número par por 2 e a divisão será exata.
Os números pares são 0,2,4,6,8,…
2) Critério de divisibilidade por 3:
Um número será divisível por 3 se a soma de seus algarismo for divisível por 3.
Complicou? Vamos explicar:
Se tivermos 8181 dividido por 3, como saber se essa divisão será exata?
Somamos os algarismos 8 + 1 + 8 + 1 = 18.
18 é divisível por 3? Sim, pois 3 x 6 = 18 então 18 ÷ 3 = 6.
Critério de divisibilidade por 4: um número para ser divisível por 4 tem seus dois últimos algarismos múltiplos de 4.
Ex: 188, 212, 128, 176
Como dizemos, os dois últimos algarismos são da tabuada do 4.
3) Critério de divisibilidade por 5:
Um número só é divisível por 5 quando terminar em zero ou em 5.
Exemplos: 800, 965, 730… todos esses números se divididos por 5 teremos um resto zero na divisão.
4) Critérios de divisibilidade por 6:
Um número para ser divisível por 6 tem que ser divisível por 3 e por 2.
Exemplo:
156 é par é divisível por 2.
A adição entre seus algarismos é: 1 + 5 + 6 = 12 que é divisível por 3.
Então 156 é divisível por 6.
No site e no blog da OBMEP tem muito material legal para você aprofundar seus estudos em Matemática. Sobre divisibilidade, tem um artigo no Clube de Matemática da OBMEP bem legal.
5) Critérios de divisibilidade por 7:
Para descobrirmos se um número é divisível por 7, temos que seguir as seguintes etapas:
1) Primeira etapa: Multiplicar por 2 o último algarismo do número que vamos analisar.
2) Segundo etapa: Diminuir o resultado obtido (na primeira etapa) do número inicial sem o último algarismo.
3) Repetir as etapas acima até termos um resultado de um ou dois algarismos.
4) Observar se o resultado é um múltiplo de 7.
Exemplo: O número que vamos analisar e descobrir se é divisível por 7 é 6481 .
a) O último algarismo é 1, então vamos multiplicar por 2: 1 X 2 = 2
b) Temos agora que diminuir o resultado do número inicial sem o último algarismo. O número inicial sem o algarismo 1 é 648. Vamos subtrair 2 desse número: 648 – 2 = 646
c) Como o resultado que obtivemos tem três algarismos, precisaremos repetir as etapas iniciais.
Multiplicaremos por 2 o último algarismo do número ¨646: 6 X 2 = 12
d) Subtraímos 12 do número inicial que é 64: 64 – 12 = 52
e) Veja se o resultado é um múltiplo de 7. Não existe 52 como resultado na tabuada do 7 então, não é múltiplo de 7.
Se nessa etapa final o resultado 7, 14, 21, 28, 35, 42, 49, 56, 63 ou 70, o número seria divisível por 7.
6) Critério de divisibilidade por 8:
Um número será divisível por 8 quando seus três últimos algarismos for:
a) for múltiplo de 8. Exemplo: 12816
b) terminar em três zeros. Exemplos: 9000.
7) Critério de divisibilidade por 9:
Um número é divisível por 9 quando a soma de seus algarismo for divisível por 9, ou melhor, que a soma de seus algarismos é um múltiplo de 9.
Exemplo: Determine se o número 818181 é divisível por 9:
Primeiro adicionamos os algarismo do número 818181:
8 + 1 + 8 + 1 + 8 + 1 = 27
A soma deu 27 que é o resultado do produto 3 X 9. Então 27 é múltiplo de 3 e 9, isso quer dizer que 27 é divisível por 9.
8) Critérios de divisibilidade por 10:
O número para ser dividido por 10 tem que terminar em zero. Ex: 100, 230, 7560.
Nesta aula você aprendeu o que é uma divisão exata ou não exata, o que é um múltiplo, os critérios para descobrir se um número é divisível ou não por seu divisor, aprendeu que um número é divisível por outro se a divisão entre eles é exata.
Exercícios sobre critérios de divisibilidade
.
Referências:
GIOVANNI JR, José Ruy; CASTRUCCI, Benedito. A Conquista da Matemática, 6º ano. São Paulo: FTD, 2009.
LIMA; Maria Cristina Ponciano de; TINANO, Marilene Turibia de Rezende. Matemática, 6º ano: Ensino Fundamental 2, livro 1 – Belo Horizonte: Educacional, 2015.
Imagens: Freepick.com e Wikimedia Commons.