Números decimais: entenda o que vem depois da vírgula
Números com vírgula são Números Decimais. Eles dão um nós na sua cabeça? Então, todo dia você encontra os números decimais no preço da gasolina, nas compras do supermercado, ou cotações de moedas. Eles são os números expressos por casas decimais depois da vírgula. Aprenda agora como resolver questões com números decimais.
Quando você vai ao supermercado a maior parte dos produtos têm preços com números que contém vírgula, com duas casas decimais e, muitas vezes, terminados em 99. Esses preços são representados por números decimais.
Os números que mais lidamos são os decimais. Por isso, saber operá-los é muito importante para que não haja perdas significativas no seu bolso, por exemplo.
Os Números Decimais e as representações
Comece pela introdução simples e rápida do professor Lucas Borguezan, do canal do Curso Enem Gratuito. Domine os números decimais, que são os números com vírgulas, para resolver e gabaritar nas questões das provas:
Mas nem sempre um número decimal é representado através da vírgula e casas decimais, já que um número inteiro também faz parte desse conjunto de números.
Veja que o peso de um saco de arroz de 5kg pode ser expresso em reais e ser um número inteiro como 13 reais ou R$ 13,00. Entenda que a função da vírgula é a de separar a parte inteira da parte decimal.
Para que você compreenda melhor vamos explicar alguns conceitos básicos:
O que é Fração Decimal:

Observe os denominadores das frações apresentadas e veja que o que elas têm em comum são seus denominadores múltiplos de 10.
Para transformar números decimais em frações decimais, devemos escrever no numerador o número decimal sem a vírgula e, no denominador, o algarismo 1, seguido de tantos zeros quantas forem as casas decimais esse número tem. Vamos a alguns exemplos?
Você pode perguntar: e como faço para transformar frações em números decimais? Nesse caso, as frações decimais podem ser transformadas em números decimais escrevendo o numerador da fração com tantas casas decimais quantos forem os zeros do denominador. Vamos a alguns exemplos:
![]()
Veja que esse número dado tem 3 casas decimais, isto é, três algarismos após a vírgula. Então, o denominador será o algarismo 1 seguido de 3 zeros.
![]()
Neste caso, temos uma parte inteira que é o algarismo 1 seguido de duas casas decimais. Escrevemos no numerador da fração todo o número dado sem a vírgula. No denominador colocamos o algarismo 1 seguido de dois zeros. ( que correspondem às duas casas decimais.)
O que é uma Fração?
Uma Fração corresponde a uma parte determinada de um todo. É um pedaço. Por exemplo, em uma pizza dividida em seis fatias iguais, cada fatia representa uma fração de 1/6 (um sexto) do todo. Veja o resumo de Fração como professor Lucas:
Números decimais e frações equivalentes:
Podemos também transformar um número decimais em várias frações equivalentes. Observe esse exemplo:
![]()
Se multiplicarmos o numerador e o denominador da fração acima sempre por 10, temos:
![]()
Assim, encontramos algumas frações equivalentes, porque essa multiplicação pode ser infinita. O que nos interessa é mostrar que se dividirmos cada uma delas retornaremos a seu valor original que é 2, 25.
Sempre encontraremos o mesmo valor. Essa é uma propriedade importante dos números decimais.
Dica: Para relembrar das potências de dez acesse o artigo: Potências de dez – Revise Matemática.
Adição e Subtração com números com vírgula:
Para adicionarmos ou subtrairmos dois números decimais precisamos lembrar que:
- Esses números têm que ter a mesma quantidade de casas decimais, para isso temos que colocar zeros para completar as casas decimais dos números que tem menos,
- As vírgulas devem ser colocadas umas embaixo das outras,
- Agora basta somar ou subtrair normalmente, mantendo a vírgula no mesmo alinhamento.
Observe o exemplo: 17,321-13,9=
Precisamos armar esse cálculo:
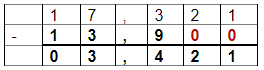
Veja que colocamos zeros na segunda parcela da adição para que ficasse com 3 algarismos após a virgulas ou seja 3 casas decimais. Então 17,321-13,9=3,421
Multiplicação
A multiplicação entre números decimais, precisamos multiplica-los como se fossem números inteiros. Após obtermos o resultado, contamos tantas casas decimais da direita para a esquerda. Essas casas decimais devem ser iguais a soma do número de casas decimais do primeiro número com o número de casas decimais do segundo número (fator).
Vamos mostrar um exemplo:
8,2×5,25=
O primeiro fator (81,2) tem uma casa decimal enquanto o segundo fator (5,25) tem duas casas decimais, logo o produto (resultado) deve ter 1 + 2 = 3 algarismos após a vírgula.
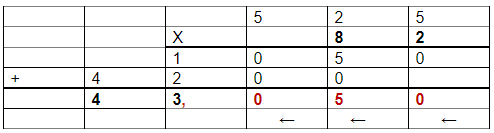
Após a multiplicação contamos de trás para a frente o número de casas decimais e colocamos a vírgula a frente da última casa contada, que nesse caso é o número zero. Então 8,2×5,25=43,050
Divisão de números com vírgula
A divisão entre números decimais depende de alguns detalhes:
- Se o número de casas decimais dos números que serão divididos não for igual temos que igualar acrescentando zeros;
- Após igualarmos as casas decimais nos livramos das vírgulas;
- Dividimos normalmente como aprendemos com números inteiros.
Acompanhe o exemplo:
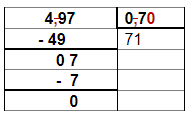
Para compreender melhor a divisão assista ao vídeo de nosso colega Rafael Procópio e aprenda muito mais:
Lembramos que os números decimais e suas operações aparecem associadas a outras aplicações como regras de três, transformações de unidades e na interpretação gráfica. Revise sempre os conteúdos básicos que são as chaves de seu sucesso!
Agora é com você! Resolva as questões abaixo e pratique.
1. (Enem 2013) Uma torneira não foi fechada corretamente e ficou pingando, da meia noite até as seis horas da manhã, com a frequência de uma gota a cada três segundos. Sabe-se que cada gota d’água tem volume de 0,2mL. Qual foi o valor mais aproximado do total de água desperdiçada nesse período em litros?
a) 0,2
b) 1,2
c) 1,4
d) 12,9
e) 64,8
2. (CESGRANRIO) Um automóvel percorre 400km, consumindo 44l de álcool. Se o preço do álcool fosse de R$0,50, o proprietário do automóvel gastaria , em média por quilômetro percorrido, a quantia de:
a) R$ 0,044.
b) R$ 0,045.
c) R$ 0,050.
d) R$ 0,055.
3. (UNIRIO) Suponha que um carro movido à gasolina consiga , em média, percorrer 10km por litro e, um carro movido a álcool, apenas 8km por litro.
Se o litro da gasolina fosse R$ 0,60, quanto deve custar o litro do álcool para que os veículos sejam igualmente econômicos?
a) 0,38.
b) 0,48.
c) 0,42.
d) 0,45.
Gabarito:
1. C;
2. D;
3. B.
Simulado de números decimais
Referências Bibliográficas:
MORAES, J. L. de. Matemática e Lógica para Concursos. São Paulo: Saraiva, 2013.
MOREIRA, Alexandre. FLUMIAN, Renan. GARCIA, Wander. Como se dar muito bem no ENEM. São Paulo: Ed. Foco Jurídico, 2016.





