Estudo dos triângulos: classificações, características e propriedades
Nesta aula você vai aprofundar o estudo sobre triângulos, seus elementos, classificações quanto a seus lados e quanto a seus ângulos e sua condição de existência. Vai aprender ainda o que são triângulos congruentes e dominar o famoso triângulo retângulo.
E você sabe porque você precisa revisar tudo isso sobre os Triângulos? Porque já caiu várias vezes no Enem e com certeza vão aparecer questões nas provas de vestibulares das principais Universidades!
A Matemática é uma ciência cheia de surpresas e aplicações, não é mesmo? A estabilidade é a palavra de ordem nos estudos da Geometria. E existem muitas aplicações no uso de triângulos.
Introdução aos Triângulos
Veja agora como professor de matemática Sérgio Sarkis, do canal do Curso Enem Gratuito, os fundamentos que você precisa para gabaritar as questões de classificação e propriedades dos Triângulos.
A principal característica do triângulo você conferiu no resumo do professor Sarkis, que é a de possuir três ângulos internos e três ângulos externos. Além disso, ele é um polígono que possui três vértices A, B e C, e também possui três lados: AB, AC e BC.
Características dos triângulos
Para compreendermos as características dos triângulos, vou descrever para você, em linguagem matemática, essa figura geométrica.
Confira as características dos triângulos na imagem a seguir: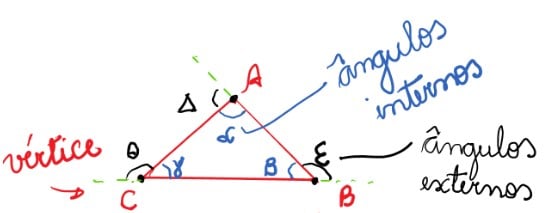 Viu que temos sempre TRÊS ÂNGULOS? Por isso o nome TRIÂNGULO = TRI ( três) + ÂNGULO.
Viu que temos sempre TRÊS ÂNGULOS? Por isso o nome TRIÂNGULO = TRI ( três) + ÂNGULO.
Elementos do triângulo
Como você pode ver no esquema, os principais elementos de um triângulo são os lados, vértices e ângulos (internos e externos).
Ângulos de um triângulo
Quanto aos ângulos, devemos saber que a soma dos ângulos internos de um triângulo é igual a 180°.
Isso significa que cada ângulo externo é suplementar ao ângulo interno adjacente e, sendo assim, a soma de suas medidas também é 180°.
Mediana, bissetriz e altura
A mediana, a bissetriz e a altura também são elementos de um triângulo.
Mediana
É o segmento de reta que une um vértice ao ponto médio do lado contrário a ele. Uma aplicação desse conceito é o baricentro, que é o centro de equilíbrio do triângulo.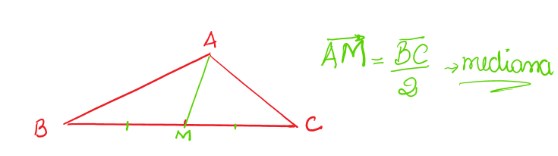
Bissetriz
A bissetriz é o segmento de reta que divide ao meio um dos ângulos internos do triângulo.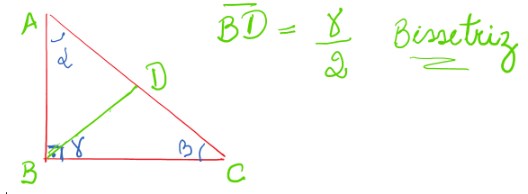
Altura
Por sua vez, a altura do triângulo é segmento de reta que une perpendicularmente (formando 90°) um dos vértices ao seu lado contrário.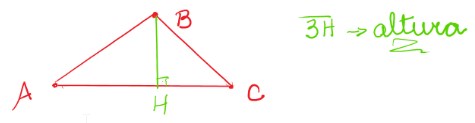
Classificação dos triângulos
Os triângulos são classificados quanto as medidas de seus lados e também quanto à medida de seus ângulos.
Quanto à medida de seus lados
A classificação dos triângulos quanto à medida dos seus lados é feita em triângulos isósceles, equilátero e escaleno.
Triângulo isósceles
São triângulos que tem dois lados com medidas idênticas e o outro com medida distinta.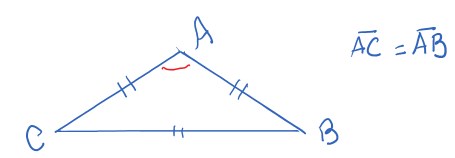
Triângulo equilátero
Triângulo equilátero é aquele que tem todos os lados com mesma medida. Ou seja, AB = BC = CA.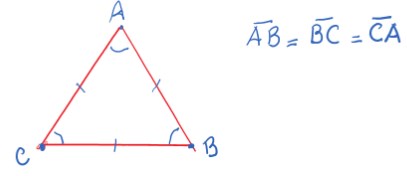
Triângulo escaleno
Por fim, o triângulo escaleno é aquele que tem todos os lados com medidas diferentes.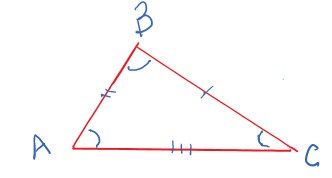
Quanto à medida de seus ângulos
Também podemos fazer a classificação dos triângulos quanto à medida dos seus ângulos. Aqui, os triângulos podem ser acutângulos, obtusângulos ou retângulos.
Acutângulo
Esse triângulo tem todos seus ângulos internos agudos, ou seja, são ângulos fechados e menores que 90°. No triângulo abaixo os ângulos formados por BAC e BCA são agudos.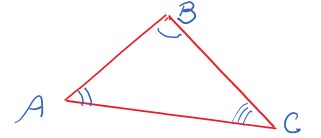
Obtusângulo
Esse triângulo tem um ângulo interno Obtuso, ou seja, tem ângulo mais aberto e maior que 90°.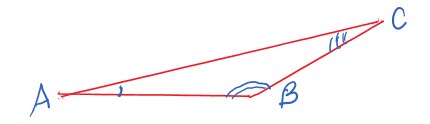 Observe que o ângulo maior é formado por ABC.
Observe que o ângulo maior é formado por ABC.
Triângulo retângulo
Esse triângulo tem um de seus ângulos internos igual a 90°.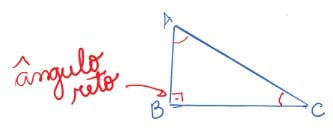
Domine o Triângulo Retângulo
O tipo de triângulo que mais aparece nas provas do Enem e dos vestibulares é o famoso Triângulo Retângulo. E, você lembra do clássico Teoremoa de Pitágoras. Mas, não custa nada lembrar dos cálculos do Triângulo Retângulo.
Tem muito mais para você aprender do que o básico de que a soma do quadrado dos catetos é igual ao quadrado da Hipotenusa. Veja agora com o professor Lucas:
Para você avançar ainda mais nessa matéria, resolva agora o simulado sobre Triângulos Retângulos.
Condição de existência de um triângulo
Para que um triângulo exista, a medida de um dos lados deve ser menor que a soma entre seus outros dois lados.
Por exemplo, se tivermos um triângulo que possua as medidas 10, 7 e 5. Para verificar se ele é um triângulo basta somar dois lados e comparar com o outro que sobrou.
Observe que se somarmos os lados 7 e 5 termos o valor 13. Esse valor é maior que o lado que sobrou: 10. Então esse triângulo existe.
Congruência de triângulos
Usamos a palavra congruência para dizer que duas medidas são iguais. No caso do estudo de triângulos são congruentes quando têm medidas dos lados iguais ou medidas de ângulos iguais.
Caso de congruência lado-lado-lado (LLL)
No caso lado-lado-lado, dois triângulos são congruentes quando possuem todos os lados com mesma medida.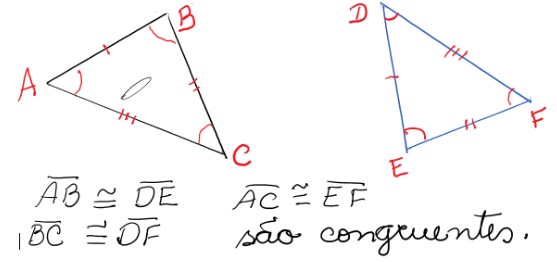
Caso de congruência lado-ângulo-lado (LAL)
Dois triângulos são congruentes quando têm dois lados iguais e o ângulo formado entre eles são iguais.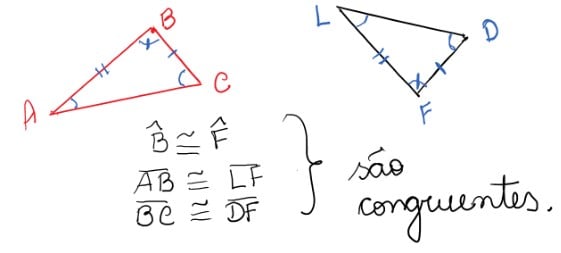
Caso de congruência ângulo-lado-ângulo (ALA)
Dois triângulos são congruentes quando têm dois ângulos e o lado adjacente a eles são iguais.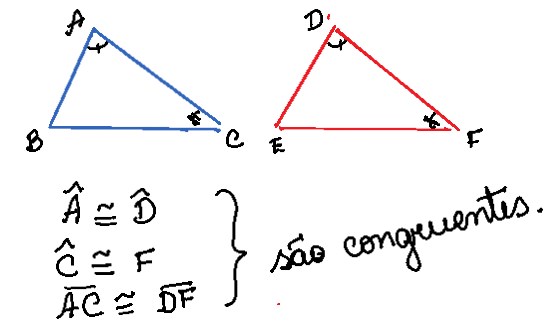
Como você pode perceber, nós trouxemos aqui a teoria sobre os triângulos e, principalmente, suas características e propriedades.
Essas informações darão uma base sólida para a resolução de vários exercícios envolvendo essas figuras planas rígidas que são tão importantes em nossos estudos. Agora, é com você!
Cálculo da Área dos Triângulos
Veja agora com o professor Lucas Borguezan os segredos para você gabaritar nas questões de cálculo de área:
Exercícios
.





