O que são números primos e como fazer sua fatoração
Saiba agora como fazer a Fatoração; o que são os Números Primos, para que eles servem, e como resolver questões de Matemática Básica para se garantir nas provas do Enem.
O estudo dos números primos nos dá uma outra perspectiva do conceito de número. Vamos apresentar a você o que são os números primos e os números naturais. Além disso, você vai aprender a usar o conceito de números divisíveis, conjunto de divisores, os critérios de divisibilidade, como fazer uma fatoração de um número composto.
O que são números primos
Um número natural é denominado primo quando:
– for maior que 1,
– for divisível somente por 1 e por ele mesmo.

Então se tivermos um número P, ele será primo se, e somente se, o número de divisores de P, for igual a 2.
Para você compreender melhor, vamos analisar se o número 11 é ou não um número primo. Em primeiro lugar, temos que determinar o conjunto de números naturais divisíveis por ele:
D(11) = {1,11}
Podemos dizer que o número de divisores de 11 é: n[D(11)] = 2. Isso porque esse número tem somente dois divisores: 1 e 11.
Está difícil de entender ainda? Então vamos fazer uma analogia: pense em uma pizza. Imagine que essa pizza tem um tamanho médio com 11 fatias e que você quer dividi-la com um grupo de amigos. A divisão não será exata independentemente da quantidade de pessoas. Uma amigo ficará com uma fatia a mais, não é mesmo?
As possibilidades de termos a divisão exata dessa pizza é se apenas uma pessoa ficar com todas as fatias ou se dividirmos essa pizza para 11 pessoas. Por isso, 11 é um número primo.
A condição necessária para identificarmos um número primo é que a divisão entre os números considerados seja inexata.
Os números primos são 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47…
Resumo sobre números primos
Veja agora com o professor Lucas Borguezan, do canal do Curso Enem Gratuito, uma introdução para você aprender a identificar os números primos!
Número composto
Se você dividir um número por outros números além de 1 e dele mesmo e o resultado for exato, você terá um número composto.
Sendo assim, “A” é um número composto, se e somente se, o número de divisores de A, ou seja
n[D(A)] > 4. (Maior que 4).
Para você entender melhor, vamos a um exemplo:
O número 12 é composto ou primo?
O conjunto dos divisores de 12 é: D(12) = {1, 2, 3, 4, 6, 12}
Logo, temos n[D(A)] = 6 e o número 12 é composto pois é divisível por 6 números. E, 6 > 4.
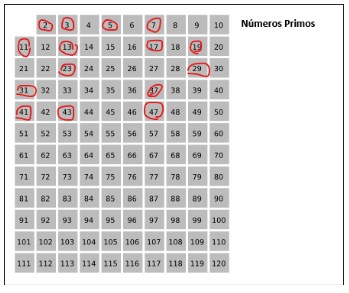
Método de Erastóstenes
Os números primos ainda podem ser identificados pelo Método de Erastóstenes.
Erastóstenes de Cirene ( 276 a.C. – 194 d.C.) foi um astrônomo, matemático, geógrafo e filósofo (entre outras atividades) que viveu na Grécia Antiga, tendo também sido chefe bibliotecário na famosa Biblioteca de Alexandria.
Ele elaborou um passo a passo para descobrirmos os números primos:
- Escrevemos os números de 1 a 50 ou o limite que você quiser.
- Riscamos o número 1 que não é primo.
- Circulamos o número 2.
- Riscamos todos os números divisíveis por 2.
- Circule o próximo número: 3.
- Riscamos todos os números divisíveis por 3.
- Continuamos circulando o próximo número e riscando seus divisíveis até o final da tabela.
Fatoração ou decomposição em fatores primos
Confira o resumo inicial com o professor Lucas, do canal do Curso Enem Gratuito, para você compreender o conteúdo de fatoração:
Decompor um número em fatores primos é o mesmo que reescrever esse número em forma de produto (multiplicação), onde todos os fatores desse produtos são primos.
Um exemplo simples: 12 pode ser escrito de diversas formas:
12 = 2 x 6 ( O número seis é composto.)
Temos que reescrever o número 6 através de um produto de números primos também:
12 = 2 x 2 x 3.
Essa é a decomposição em fatores primos do número 12. Ainda podemos escrever os fatores que se repetem em forma de potência:
12 = 2² x 3. Pronto! Fácil, não é mesmo?
A regra para fatoração é simples: dividimos o número composto pelo seu menor divisor primo. O resultado pelo menos número primo seguindo os critérios de divisibilidade.
Continue a dividir até chegarmos ao resultado igual a 1. Os divisores usados são escritos em forma de produto e temos a fatoração.
Veja o exemplo abaixo:

Nessa aula, você aprendeu que:
- Um número primo é divisível somente por 1 e por ele mesmo.
- Um número é primo se sua divisão for inexata.
- Erastóstenes foi um matemático que determinou um método para identificar os números primos.
- Só um número composto pode ser fatorado.
- A fatoração de um número composto nada mais é que uma decomposição do número. Uma multiplicação de fatores primos.
Exercícios sobre Números Primos
1) Quais dos números abaixo são compostos?
A) 81
B) 227
C) 463
D) 101
E) Nenhuma das respostas acima.
2) A fatoração que melhor representa o número 1386 é:
A) 2 . 3² . 7 . 11
B) 2³ . 3² . 5
C) 2² . 3 . 5 . 7
D) 2 . 5 . 7 . 41
E) 2 . 5 . 41
3) A forma fatorada 2² . 3² . 5 . 7 é do número:
A) 96
B) 324
C) 1024
D) 1260
E) 2870
Gabarito:
1 – A, 2 – A, 3 – D.
Referências:
GIOVANNI JR, José Ruy; CASTRUCCI, Benedito. A Conquista da Matemática, 6º ano. São Paulo: FTD, 2009.
CENTURIÓN; Marília; JAKUBOVIC, José Rezende. Matemática Teoria e Contexto, 6º ano – São Paulo: Saraiva, 2015.
Imagens: Portal e- UNICAMP.





