Como fazer a fatoração de uma expressão algébrica

Nesta aula você vai revisar caso a caso como fatorar uma expressão algébrica. Para isso, estudaremos fator comum, fatoração por agrupamento, diferença entre dois quadrados e o trinômio quadrado perfeito.

O que é fatoração?

Fatoração é um novo modo de reescrever uma expressão em forma de produto. Confira uma introdução com o professor Lucas, do canal do Curso Enem Gratuito, e depois acompanhe a aula completa, com todas as dicas, exemplos e exercícios resolvidos.

Veja o exemplo a seguir para uma melhor compreensão sobre Fatoração:

Se tivermos uma expressão algébrica desse tipo:Podemos afirmar que:

1. a variável  aparece nos dois termos da expressão.
2. podemos escrevê-la em forma de produto colocando a variável  em evidência.
3. Veja como fica: 

Veja que isso pode facilitar a resolução de uma expressão. Assim, quando podemos reescrever uma expressão algébrica em forma de produto estamos fatorando a expressão.

Tipos de fatoração

Fator comum:

Dizemos que colocamos o fator que se repete em todos os termos da expressão em evidência, como mostramos no exemplo anterior. Quer mais um exemplo? Vamos lá!

Temos mais que um termo que se repete aqui. Vamos reescrever a expressão para você entender:

Reescrevemos a expressão toda em forma de produto e deixamos em vermelho os termos que se repetem nos dois termos da expressão. Agora é só colocar em evidência:

Está pronto! Observe que em vermelho são os termos que repetem e em preto são os termos que sobraram.

Agrupamento:

Para fatorar um polinômio por agrupamento temos que:
Identificar os termos que têm variáveis e números em comum.

Agrupar esses termos

Usar o método do fator comum.
Agrupar os fatores em comum.
Escrever em forma de produto.

Complicou? Nada! É fácil. Vamos colocar em prática? Veja o seguinte polinômio:

Vamos descobrir os fatores comuns:

Agora vamos colocar os fatores comuns em evidência:

Precisamos agrupar os fatores em evidência:

Ainda temos um fator comum, vamos fatorar:

Viu? Não é tão complicado quando parece. A fatoração rapidinho está completa.

Diferença entre dois quadrados:

Neste caso temos uma operação inversa aos produtos notáveis.
O produto notável em questão aqui é o produto da soma pela diferença e sua forma geral é: 

Um exemplo desse tipo de fatoração é 

Para resolver esse tipo de fatoração basta extrair a raiz quadrada de cada termo: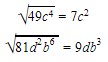

Agora é só colocar no formato inverso do produto notável:E está pronta a fatoração dessa expressão.

Trinômio quadrado perfeito

É o inverso do quadrado da soma ou o quadrado da diferença:Veja como fazer:

Identifique o termo do meio como duas vezes o primeiro pelo segundo.
Identifique se é soma ou diferença.
Extraia a raiz quadrada do primeiro e último termo do polinômio.

Vamos para a prática:

O termo do meio é:O sinal do termo do meio é negativo, isso é quadrado da diferença.

A raiz quadrada do primeiro termo é:

A raiz quadrada do último termo é:

Basta montar o produto notável:Essas dicas são importantes para você! Nas provas do Enem e do vestibular esses temas são usados como ferramentas para a resolução de problemas envolvendo geometria, estatística entre outros.

Veja mais sobre os produtos notáveis com as videoaulas do nosso canal

Muito bom este resumo do professor Lucas. Vale a pena ver de novo.

Resolva os exercícios para fixar o conteúdo:

Simulado de Fatoração

Limite de tempo: 0

Sumário do Quiz

0 de 10 questões completadas

Perguntas:

1. 1
2. 2
3. 3
4. 4
5. 5
6. 6
7. 7
8. 8
9. 9
10. 10

Information

.

Você já fez este questionário anteriormente. Portanto, não pode fazê-lo novamente.

Quiz is loading...

You must sign in or sign up to start the quiz.

Para iniciar este questionário, você precisa terminar, antes, este questionário:

Resultados

0 de 10 perguntas respondidas corretamente

Seu tempo:

Acabou o tempo

Você conseguiu 0 de 0 pontos possíveis (0)

Pontuação média
Sua pontuação

Categorias

1. Sem categoria 0%

Registrar seu resultado no ranking de pontuações

Carregando

Nome: E-Mail:

Captcha:

1. 1
2. 2
3. 3
4. 4
5. 5
6. 6
7. 7
8. 8
9. 9
10. 10

1. Respondido
2. Revisão

1. Pergunta 1 de 10

   1. Pergunta

   (ESPM SP/2019)    

   O número que se deve somar a 456 788² para se obter 456 789² é:

   • 456 789
   • 1
   • 456 788
   • 913 579
   • 913 577
   Correto
   

   Parabéns! Siga para a próxima questão.

   Incorreto
   

   Resposta incorreta. Revise o conteúdo nesta aula sobre fatoração para acertar na hora da prova!
2. Pergunta 2 de 10

   2. Pergunta

   (ESPM SP/2018)    

   O valor numérico da expressão 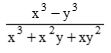 para x = 0,8 e y = 0,3 é igual a:

   • 0,325
   • 0,125
   • 0,415
   • 0,625
   • 0,275
   Correto
   

   Parabéns! Siga para a próxima questão.

   Incorreto
   

   Resposta incorreta. Revise o conteúdo nesta aula sobre fatoração para acertar na hora da prova!
3. Pergunta 3 de 10

   3. Pergunta

   (UTF PR/2018)    

   Dados A = x + y, B = x – y e C = xy, para x ≠ y, x ≠ 0 e y ≠ 0. Simplificando a expressão algébrica 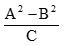, obtém-se:

   • 0.
   • 
   • 4.
   • 
   • 
   Correto
   

   Parabéns! Siga para a próxima questão.

   Incorreto
   

   Resposta incorreta. Revise o conteúdo nesta aula sobre fatoração para acertar na hora da prova!
4. Pergunta 4 de 10

   4. Pergunta

   (UTF PR/2017)    

   Uma indústria fabrica uma placa metálica no formato de um retângulo de lados (ax + by) e (bx + ay).

   Encontre, de forma fatorada, o perímetro deste retângulo.

   • 2(a + b)(x + y).
   • 4(a + b)(x + y).
   • 2(a – b)(x – y).
   • 4(a – b)(x – y).
   • (a + b)(x + y).
   Correto
   

   Parabéns! Siga para a próxima questão.

   Incorreto
   

   Resposta incorreta. Revise o conteúdo nesta aula sobre fatoração para acertar na hora da prova!
5. Pergunta 5 de 10

   5. Pergunta

   (UTF PR/2017)    

   Um fazendeiro possui dois terrenos quadrados de lados a e b, sendo a > b. Represente na forma de um produto notável a diferença das áreas destes quadrados.

   • (a + b).(a + b)
   • (a + b).(a – b)
   • (a – b).(a – b)
   • (a + b)2
   • (a – b)2
   Correto
   

   Parabéns! Siga para a próxima questão.

   Incorreto
   

   Resposta incorreta. Revise o conteúdo nesta aula sobre fatoração para acertar na hora da prova!
6. Pergunta 6 de 10

   6. Pergunta

   (IFSC/2017)    

   Após analisar as afirmações a seguir sobre produtos notáveis e fatoração, marque com (V) o que for verdadeiro e, com (F), o que for falso.

   (   )   (3a² – 2b)² = 9a⁴ – 12a²b + 4b²

   (   )   (a – b)³ = a³ – b³

   (   )   64a² – 49b² = (8a – 7b)(8a + 7b)

   (   )   4a² – 16b² = (2a – 4b)²

   (   )   a³ + b³ = (a + b)(a² – ab + b²)

   Assinale a alternativa que contém a ordem CORRETA de preenchimento dos parênteses, de cima para baixo.

   • V,F,V,F,V
   • V,V,F,F,F
   • V,F,V,V,F
   • F,F,V,V,V
   • F,V,F,V,V
   Correto
   

   Parabéns! Siga para a próxima questão.

   Incorreto
   

   Resposta incorreta. Revise o conteúdo nesta aula sobre fatoração para acertar na hora da prova!
7. Pergunta 7 de 10

   7. Pergunta

   (IFAL/2017)    

   Determine o valor do produto (3x + 2y)², sabendo que 9x² + 4y² = 25 e xy = 2.

   • 27.
   • 31.
   • 38.
   • 49.
   • 54.
   Correto
   

   Parabéns! Siga para a próxima questão.

   Incorreto
   

   Resposta incorreta. Revise o conteúdo nesta aula sobre fatoração para acertar na hora da prova!
8. Pergunta 8 de 10

   8. Pergunta

   (FUVEST SP/2016)    

   A igualdade correta para quaisquer a e b, números reais maiores do que zero, é

   • 
   • 
   • 
   • 
   • 
   Correto
   

   Parabéns! Siga para a próxima questão.

   Incorreto
   

   Resposta incorreta. Revise o conteúdo nesta aula sobre fatoração para acertar na hora da prova!
9. Pergunta 9 de 10

   9. Pergunta

   (UFRGS/2016)    

   Se x + y = 13 e xy = 1, então x² + y² é

   • 166.
   • 167.
   • 168.
   • 169.
   • 170.
   Correto
   

   Parabéns! Siga para a próxima questão.

   Incorreto
   

   Resposta incorreta. Revise o conteúdo nesta aula sobre fatoração para acertar na hora da prova!
10. Pergunta 10 de 10

    10. Pergunta

    (UNIUBE MG/2016)    

    É comum, na matemática, escrever um número em função de outro. Esse tipo de relação permite, muitas vezes, simplificar a escrita matemática, facilitando, assim, as operações algébricas. Vamos ver se você domina esse artifício matemático?

    Sendo 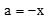,  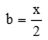e 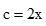, a expressão  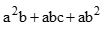tem como resultado:

    • 
    • 
    • 
    • 
    • 
    Correto
    

    Parabéns! Siga para a próxima questão.

    Incorreto
    

    Resposta incorreta. Revise o conteúdo nesta aula sobre fatoração para acertar na hora da prova!

Compartilhe: