Propriedades das inequações: entenda como resolver

A diferença principal entre equação e inequação é basicamente que a equação representa uma igualdade e a inequação representa uma desigualdade. Mas o que isso significa?

Enquanto nas equações o que se busca é encontrar um resultado único para a incógnita (um resultado se for equação do primeiro grau, dois resultados se for do segundo grau, etc.), nas inequações este resultado pode ser um conjunto aberto ou fechado de números, identificados pelos símbolos de desigualdade.

Nessa aula você vai ver que para o estudo das inequações é fundamental ter em mente alguns conceitos de álgebra e de geometria analítica.

Isso porque esses conjuntos de resultados são dados ao solucionar a parte algébrica das inequações juntamente com o estudo de sinal na reta numérica. Preste atenção aos detalhes e ao final da aula resolva os exercícios para chegar com tudo na hora da prova do Enem e vestibulares!

O que é uma inequação

Uma inequação é uma sentença matemática que apresenta uma ou mais incógnitas. Veja agora com o professor Lucas Borguezan, do canal do Curso Enem Gratuito:

Como vimos acima no vídeo, uma Inequação é bem parecida com uma equação.

A principal diferença é que a equação representa uma igualdade e a inequação representa uma desigualdade. Ficou difícil? Vamos utilizar uma equação de primeiro grau como exemplo para você entender melhor. Veja:

ax+b=0

Na equação apresentada acima buscamos encontrar os valores de  que satisfazem a igualdade. Isto é, valores que tornam a equação “igual a zero”. Agora, em uma inequação, como esta:

ax+b>0

Buscamos encontrar os valores de  que satisfazem a desigualdade. Ou seja, encontrar todos os valores que fazem com que o termo ax+b  seja maior do que zero.

O símbolo  (lê-se maior que) é apenas uma das representações de uma inequação. Ainda podem ser utilizados os seguintes sinais de desigualdade:

Para demonstrar alguns exemplos e propriedades das desigualdades, vamos utilizar a inequação de primeiro grau como referência.

Resolução e propriedades de inequação do primeiro grau

Para solucionar uma inequação de primeiro grau utilizamos estratégias parecidas com as utilizadas em solução de equações.

Importante: as propriedades abaixo ilustradas valem para todo tipo de inequação que você possa vir a estudar no futuro, não somente em inequações de primeiro grau.

Exemplo a)

Resolva a inequação

Para resolver essa inequação o intuito é “isolar o x” . E, para isso, efetuaremos da mesma forma dos dois lados da desigualdade. Então, o primeiro passo é somar 18 unidades dos dois lados da desigualdade

Resultando em:

Essa operação nos remete a uma propriedade que nos diz que:

• Somar ou subtrair qualquer número ou incógnita (positivo ou negativo) nos dois membros de uma inequação não altera o sentido da desigualdade.

Continuando a operação, temos que dividir os dois lados da equação por 3, resultando em:

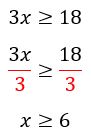
Disso discorre a seguinte propriedade:

• Multiplicar ou dividir um número positivo em ambos os membros de uma inequação não altera o sentido da desigualdade.

O interessante nessa propriedade é perceber que, desde que o número seja positivo, não importa se ele é inteiro ou não, tendo em vista que “dividir por 3” é equivalente a “multiplicar por 1/3″.

Dando seguimento à resolução, chegamos então ao resultado

Isso significa que os valores que x pode assumir e que satisfazem a inequação , são todos os valores maiores e iguais a 6. O conjunto solução é dado por:

A solução também pode ser escrita na notação de intervalos reais ou representado na reta real como:

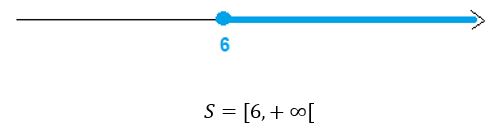
(o intervalo é fechado pois representa a desigualdade:  ≥ que inclui todos os números maiores que 6 incluindo o 6)

Exemplo b)

Como resolver a inequação ?

Utilizando estratégias para isolar o x podemos subtrair 2x dos dois lados da inequação

Resultando em

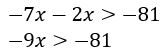
Agora, vamos multiplicar toda a inequação por (-1). Para tanto, trocamos o sinal de todos os termos, invertendo a desigualdade:

Aqui se apresenta outra propriedade das operações com inequações:

• Multiplicar ou dividir um número negativo (inteiro ou não) em ambos os membros de uma inequação inverte o sentido da desigualdade.

Em seguida, dividimos todos os termos da inequação por 9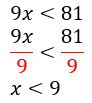
Isso significa que os valores que pode assumir e que satisfazem a inequação , são todos os valores menores que 9. O conjunto solução é dado por:

A solução também pode ser escrita na notação de intervalos reais ou representado na reta real como:

(o intervalo é aberto pois representa a desigualdade:  < que inclui todos os números menores que 9, sem incluir o 9)

Estudo de sinal

Existem algumas inequações onde, para obtermos uma solução, é necessário estudar o comportamento do sinal. Vamos solucionar a inequação

Para que essa desigualdade seja verdadeira é preciso que tanto os valores que estão no numerador quanto no denominador sejam maiores que zero. Logo, representamos cada um deles na reta real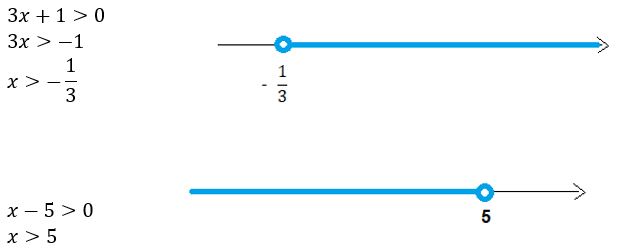

Os valores destacados em azul que aparecem tanto na primeira quanto na segunda reta real são:

(o intervalo é aberto pois representa a desigualdade: < )

Logo o conjunto solução da inequação

é

Para finalizar os estudos, assista ao vídeo do professor Lucas no nosso canal no YouTube!

Exercícios:

Questão 01)    

Dadas as funções reais f(x) = x e , o conjunto-solução da inequação f (x) ≤ g (x) é:

a) {x ∈ R | x ≤ –1 ou x > 2}

b) {x ∈ R | x ≤ –1 ou 1 < x ≤ 2}

c) {x ∈ R | x > 1 ou x < 2}

d) {x ∈ R | x < 1 ou x ≥ 2}

e) {x ∈ R | 1 < x ≤ 2}

Gab: B

Questão 02)    

Quantos números inteiros satisfazem a inequação (3x – 25)(5 – 2x) ≥ 0?

a) 3

b) 4

c) 5

d) 6

e) 7

Gab: D

Compartilhe: