Veja os tipos mais utilizados de equações que são de 1º e 2º graus e entender como resolvê-las. Aprenda o que são coeficientes, raízes de uma equação e conjunto solução. Veja métodos mais fáceis e domine a Fórmula de Bhaskara com esse resumo gratuito.
As equações mais “famosas” no Ensino Médio e no Enem são as equações de primeiro e segundo grau, que você já resolveu inúmeras vezes ao longo da sua vida escolar. Lembra da Fórmula de Bhaskara? Então, ela está aqui nesta aula pra você.
Vamos começar com um resumo rápido sobre as Equações de 1º grau: Uma equação de 1º grau é uma expressão algébrica de grau 1 igualada a zero. Tem a seguinte forma: ax+b = 0
Onde a e b são chamados de coeficientes da equação e são números reais e x é uma variável. Parece complicado? Vamos simplificar com o resumo do professor Lucas Borguezan, do canal do Curso Enem Gratuito:
Gostou das dicas do professor Lucas? Veja agora outros jeitos para resovler as Equações também:
Como resolver uma equação de 1º grau
Vamos mostrar como se resolve uma equação de primeiro grau simples através de um exemplo:
x – 7 = 10
O que fazemos aqui? O objetivo é achar o valor da incógnita x.
1º Passo: Isolamos a variável x, isto é, passamos o “– 7” para o outro lado da igualdade com sua operação inversa. Dizemos que se o um número é negativo de um lado da expressão, passará para o outro lado da igualdade positivo.
2º Passo: Resolvemos as operações:
x = 10 +7
x = 17
Então o valor da raiz da equação x é 17 e seu conjunto solução é S = {17}.
Mais um exemplo
Agora, vamos resolver a equação de primeiro grau abaixo:
– 3x + 24 = – 12
Nesse caso, para isolar a variável teremos que fazer mais um passo, observe:
1º Passo: Isolamos a variável x, isto é, passamos o “+24” para o outro lado da igualdade com sua operação inversa. Como te ensinei ali em cima, dizemos que se o número é positivo, passará para o outro lado da igualdade negativo.
– 3x = – 12 – 24
2º Passo: Resolvemos as operações. Números com o mesmo sinal a gente soma e mantém o sinal.
– 3x = – 36
3ª Passo: O número – 3 está multiplicando a variável x e para, isolá-la, passamos este número para o outro lado da igualdade dividindo.
x = – 36/ – 3
x = +12
Na divisão aplicamos a regra de sinais: Na divisão e multiplicação, números com mesmo sinal tem resultado positivo.
Então, a raiz da equação é “+ 12” e seu conjunto solução é S = {+12}.
Domine equações de 1º grau:
Veja um resumo com o professor Sérgio Sarkis, focado nos tipos de problemas que mais caem nas questões do Enem sobre Equações.
Entendeu? Agora, podemos partir para as equações de 2º grau.
Equações de 2º grau
As equações de segundo grau são expressões algébricas de grau 2, igualadas a zero. Grau 2 porque tem uma de suas variáveis com seu maior expoente igual a 2.
Apresentam-se assim: ax² + bx + c =0
Onde a, b, c são os seus coeficientes e a tem que ser diferente de zero.
Nas equações de 2º graus chamadas de incompletas, os coeficientes b ou c são iguais a zero. Veja os exemplos:
- a) 2 x² – 10 = 0
- b) x² + 4x = 0
- c) – 5x² = 0
Como resolver equações de segundo grau
A resolução das equações de 2º grau incompletas é semelhante à resolução das equações de 1º grau. A diferença é que você terá que fazer a raiz quadrada do número após a igualdade quando tiver isolado a variável.
A Fórmula de Bhaskara
Veja as dicas para gabaritar nas questões com equações de 2º grau com a Fórmula de Bhaskara:
As equações de 2º graus completas são resolvidas por dois processos distintos:
b) Produto e Soma
A fórmula de Bhaskara
A fórmula de Bhaskara é dada por: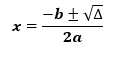
e
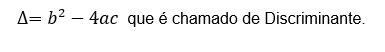
Para utilizarmos essa fórmula para resolver equações de 2º grau, o primeiro passo é “descobrir” os valores dos coeficientes da equação.
Exemplo do uso da fórmula de Bhaskara
Observe o exemplo abaixo: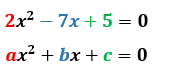
1º Passo: Descobrir os coeficientes da equação: basta comparar a equação geral com a equação que queremos resolver e temos os valores dos coeficientes:
2º Passo: Substituímos os coefientes na fórmula do Discriminante (Delta):
3º passo: Substituímos todos os valores na Fórmula de Bhaskara: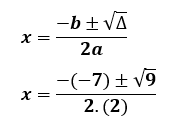
Fazendo as regras de sinais, extraindo a raiz quadrada e multiplicando os denominadores temos:
Teremos como resultado duas raízes, a primeira usando o sinal de adição entre os números + 7 e 3: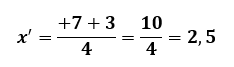
E outro resultado, subtraindo + 7 e 3: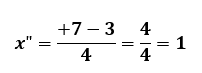
Então, o conjunto solução para essa equação completa de 2º grau tem dois valores: S = {2,5; 1}.
As equações de segundo grau são expressões algébricas de grau 2, igualadas a zero. Apresentam-se assim: ax² + bx + c =0. Quer entender direitinho como se resolve uma equação do segundo grau? Vamos seguindo com a aula para você dominar bem o assunto.
As equações de 2º grau completas podem ser resolvidas por outro método: Produto e Soma, mas esse será assunto para um outro post.
Lembramos que a principal característica de uma equação completa de 2º grau é ter dois valores de raízes. Esses valores serão solução se, e somente se, os substituirmos na equação e termos uma sentença verdadeira, isto é, 0 = 0.
Para isso basta substituirmos os valores das raízes na equação original.
Observe:
Chegamos a uma solução verdadeira. Então 2,5 é raiz da equação.
Método da soma e produto
Mais técnicas para resolver equações do 2º grau
Exercícios sobre equações de 1º e 2º graus
Questão 1 – (PUC -MG) O valor de x que é solução da equação (x/3)-(1/4)=2(x-1) pertence ao intervalo:
a) ]0, 1]
b) ]1, 2]
c) ]2, 3]
d) ]3, 4]
Questão 2 – (FATEC – SP) Sobre as raízes reais da equação x + 32/x – 12 = 0, é verdade que:
a) uma delas é o dobro da outra.
b) têm sinais contrários.
c) são maiores que 10.
d) não são inteiras.
e) são inexistentes.
Questão 3 – (Enem – 2013) A temperatura T de um forno (em graus centígrados) é reduzida por um sistema a partir do instante de seu desligamento (t = 0) e varia de acordo com a expressão com t em minutos. Por motivos de segurança, a trava do forno só é liberada para abertura quando o forno atinge a temperatura de 39 ºC. Qual o tempo mínimo de espera, em minutos, após se desligar o forno, para que a porta possa ser aberta?
a) 19,0.
b) 19,8.
c) 20,0.
d) 38,0.
e) 39,0.
Gabarito:
1 – B; 2 – A; 3 – D.
