A regra de Sarrus permite que calculemos o valor do determinante de uma matriz quadrada de ordem 3 através de suas diagonais principais e secundárias.
O método prático de solução de matrizes quadradas de ordem 3, denominado regra de Sarrus, foi desenvolvido pelo matemático francês Pierre Frédéric Sarrus. Ele é o autor de diversos tratados envolvendo equações numéricas de múltiplas incógnitas, sendo um dos nomes mais importantes na história da matemática.
O que é a regra de Sarrus
A regra de Sarrus é uma regra de memorização utilizada para encontrar o valor do determinante associado a uma matriz quadrada de ordem 3. Na verdade, quando nos referimos a uma regra de memorização, nos referimos a algo que entra na nossa memória e não sai nunca mais!
É por isso que muitos professores de cursinhos utilizam músicas em suas aulas para garantir que seus alunos lembrem de regras básicas, e que são comumente utilizadas. A regra de Sarrus não é diferente. Depois dessa aula, você vai relembrar o conceito e, toda vez que for necessário calcular o determinante, vai ter em mãos o recurso mais adequado.
O determinante de uma matriz
O determinante de uma matriz é obtido através de cálculos que associam esta matriz a um número escalar. Esse número é o próprio determinante.
Em matrizes de ordem 1, o determinante é equivalente ao único elemento da matriz. Em matrizes de ordem 2, o cálculo do determinante é dado pela diferença entre o produto dos elementos da diagonal principal pelos elementos da diagonal secundária. Já para matrizes de ordem 3, esse método não é viável, visto que “deixaria de lado” muitos termos da matriz.
Como aplicar a regra de Sarrus passo a passo
A regra de Sarrus permite que calculemos o valor do determinante de uma matriz quadrada de ordem 3 através de suas diagonais principais e secundárias. Mas como aplicar a Regra de Sarrus? Vamos ver o passo a passo por meio de um exemplo.
Exemplo
Calcular o determinante da matriz B
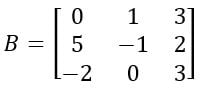
Passo 1
Copiar a primeira e a segunda colunas da matriz e reescrevê-las à direita da matriz, obtendo 5 colunas em sequência, assim:
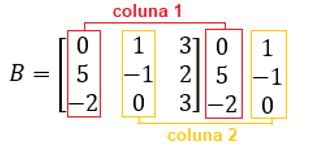
Passo 2
Determinamos quais são as diagonais principais paralelas à diagonal principal, e as diagonais secundárias paralelas à diagonal secundária. Temos um esquema da forma:
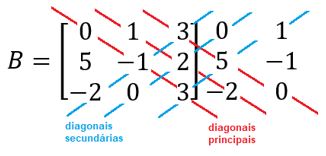
Para garantir que você selecionou as diagonais principais e secundárias corretamente, verifique se “sobraram” o primeiro e último termo na linha 2. No exemplo, “sobraram” os elementos 5 e -1, logo, está correto.
Passo 3
Encontrar a soma dos produtos dos elementos da diagonal principal e suas paralelas e a soma dos produtos dos elementos das diagonais secundárias e suas paralelas. Então:
diagonais principais: 0 . (-1) . 3 + 1 . 2 . (-2) + 3 . 5 . 0 = -4
diagonais secundárias: (-2) . (-1) . 3 + 0 . 2 . 0 + 3 . 5 . 1 = 21
Passo 4
Subtrair o valor da soma dos produtos dos elementos das diagonais secundárias do valor obtido na soma dos produtos dos termos das diagonais principais, sendo assim:
det(B) = diagonais principais – diagonais secundárias
det(B) = – 4 – 21
det(B) = -25
Pronto! Depois de apenas 4 passos, você já encontrou o valor do determinante através da regra de Sarrus.
E aí, o que você achou? Eu, particularmente, considero a regra de Sarrus um método bastante trabalhoso, mas que não envolve muita dificuldade em sua execução. Aos poucos, em seus estudos, você vai encontrar aplicação deste método em diversos tipos de problemas matemáticos.
Outro tópico que você vai encontrar bastante por aí em seus estudos, e é muito importante de se ter conhecimento, é o conceito de traço de uma matriz. Esse método leva em consideração a diagonal principal de uma matriz em seu cálculo. Acompanhe a seguir.
Traço de uma Matriz
Denominamos o traço de uma matriz quadrada como o número escalar que associa a matriz à soma dos elementos de sua diagonal principal. Em outras palavras, podemos dizer que o traço de uma matriz A é a soma de todos os elementos aij onde i = j.
tr(A) = a11 + a22 + … + anm
Exemplo:
Determine o traço da matriz A:
Sua diagonal principal é:
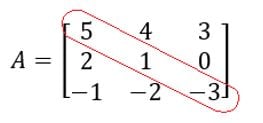
Assim, o traço é dado por:
tr(A) = 5 + 1 + (-3)
tr(A) = 3
O traço de uma matriz é um conceito que quando cai em uma prova costuma assustar pelo seu desconhecimento. Este foi um resumo simples, mas no qual consta o básico que você precisa saber caso alguma questão levante, ao mesmo tempo, o conceito de regra de Sarrus e traço de uma matriz.
Videoaula sobre a aplicação da regra de Sarrus
Para terminar seus estudos sobre a regra de Sarrus, assista à videoaula abaixo e entenda melhor como aplicá-la para resolver exercícios sobre determinantes.
Exercícios sobre a regra de Sarrus
Agora que você já entendeu tudo sobre a regra de Sarrus, resolva os exercícios a seguir, selecionados pela nossa professora!
1- (UERN/2015)
Considere a seguinte matriz A = (ij)3X3:
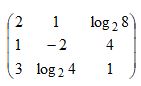
Pela regra de Sarrus, o determinante dessa matriz é
a) 8.
b) 9.
c) 15.
d) 24.
2- (UFGD MS/2013)
Sabendo que A = [aij]2×2 e aij = ij + j2 e B = [bij]3×3 e bij = ji + i2, então, o produto det(A). e det(B) é um número
a) múltiplo de 5.
b) maior que 15 e menor que 20.
c) múltiplo de 3 e 7.
d) múltiplo de 2,3,4.
e) que possui divisores {1,2,4}.
3- (Faculdade Guanambi BA/2018)
Considerando-se a matriz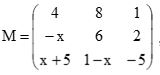 
, é correto afirmar que o menor valor real de x que anula o det M é
01. –5
02. –3
03. 0
04. 1
05. 5
Gabarito:
- C
- E
- 02
