Determinante de uma matriz: o que é e como calcular
Determinante é a transformação de todos os termos de uma matriz em um único número escalar. Veja como calcular o Determinante com os macetes da Regra de Chió.
O estudo de matrizes e determinante é imprescindível, não somente para ir bem na prova do Enem e vestibulares, mas também estar preparado para os estudos posteriores.
Determinante de uma matriz
Ao calcular o determinante de uma matriz qualquer, estamos “transformando” todos os termos de uma matriz em um único número escalar. Essa ferramenta matemática é muito utilizada no estudo e compreensão de dados de diversas áreas.
Sendo assim, é importante compreender os conceitos primeiros, independentemente de qual caminho você vai tomar depois do vestibular.
O que é uma Matriz? – A melhor dica para você começar este resumo sobre o cálculo do Determinante de uma Matriz é você fazer uma revisão bem leve sobre as características das matrizes. Veja com o professor Lucas Borguezan
Como calcular o determinante de uma matriz
Vamos começar pelo básico: aprenda a calcular o determinante de matrizes de ordem 1, 2 e 3.
Matrizes de ordem 1
Uma matriz é considerada de ordem 1 quando possui um único elemento a11. Pode ser escrita como M1 = |a11| ou M = |a11|.
Exemplos:
- M = |8|
- N = |4|
- 0 = |-1|
Para o cálculo do determinante de uma matriz de ordem 1 não é preciso nenhum esforço, o determinante desse tipo de matriz é o próprio elemento que a compõe. Nos exemplos acima:
- det(M) = 8
- det(N) = 4
- det(0) = -1
Matrizes de ordem 2
Para calcular o valor do determinante de uma matriz quadrada de ordem dois, basta considerar a diagonal principal e a diagonal secundária. Para facilitar a compreensão, substituiremos os índices em sua forma convencional:
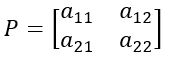
Para as letras a, b, c e d:
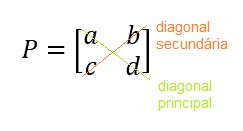
Agora, basta calcular o produto entre os elementos a e d da diagonal principal e subtrair pelo produto entre os elementos c e b da diagonal secundária. Assim, o determinante de P é dado por:
det(P) = a x d – c x d
Exemplo: calcular o determinante da matriz quadrada B:
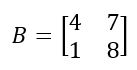
Antes de tudo, é preciso verificar qual a diagonal principal e qual a diagonal secundária. Assim,
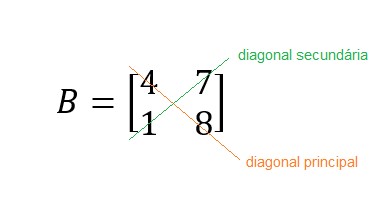
Multiplicando os elementos da diagonal principal entre si temos 4 x 8 = 32.
Multiplicando os elementos da diagonal secundária, temos 1 x 7 = 7.
Subtraindo os dois resultados: 32 – 7 = 25.
Logo, det(B) = 25.
Resumo sobre o Cálculo do Determinante
Acompanhe uma introdução rápida e bem didática com o professor de matemática Lucas Borguezan, do canal do Curso Enem Gratuito:
Bem simples, né? Mas e quando se trata de matrizes com ordem superior a 2? Bem, vejamos no tópico a seguir que o raciocínio é o mesmo.
Matrizes de ordem 3 ou superior
Para calcular o valor do determinante de matrizes de ordem 3 ou superior a 3, utilizamos um método bastante conhecido, a Regra de Sarrus, que leva o nome de seu desenvolvedor Pierre Frédéric Sarrus.
O método consiste em duplicar a primeira e a segunda coluna da matriz da qual se quer calcular o determinante. Assim:
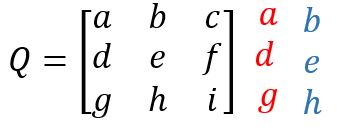
Disso resultam 3 diagonais principais, e 3 diagonais secundárias, veja:
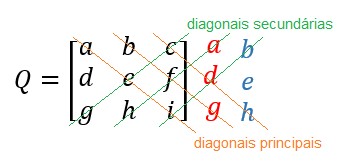
Agora, para calcular o determinante, basta multiplicar cada um dos termos de cada diagonal entre si, somando seus resultados, por exemplo, nas diagonais principais temos:
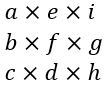
Ao somá-los, ficamos com:![]()
O mesmo é feito com os termos das diagonais secundárias, assim, temos
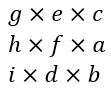
Somando os resultados, temos:
![]()
Por fim, basta realizar a diferença entre os resultados obtidos na soma das diagonais principais, e na soma das diagonais secundárias, o cálculo fica assim:
det(Q) = aei + bfg + cdh – (gec + hfa + adb)
O resultado obtido nesse cálculo é o número escalar correspondente ao determinante da matriz.
Para fixar bem essas informações, vamos resolver um exemplo numérico.
Exemplo:
Calcular o determinante da matriz
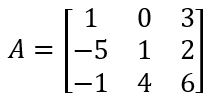
Primeiro passo, duplicar a primeira e a segunda coluna:
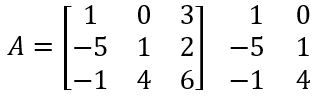
Agora, determine as diagonais principais e as secundárias:
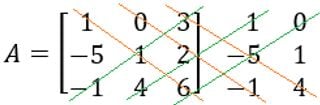
Já efetuando os cálculos de multiplicação e soma, temos:
- diagonais principais = 1 x 1 x 6 + 0 x 2 x (-1) + 3 x (-5) x 4 = 6 + 0 – 60 = -54
- diagonais secundárias = (-1) x 1 x 3 + 4 x 2 x 1 + 6 x (-5) x 0 = -3 + 8 + 0 = 5
Fazendo a subtração, temos:
det(A) = dp – ds
det(A) = -54 – 5
det(A) = -59
Então, o valor do determinante associado à matriz A é igual a -59.
A Regra de Chió
Veja como reduzir o tamanho de matrizes para facilitar o cálculo do determinante com os macetes da Regra de Chió:
Propriedades dos determinantes
As propriedades dos determinantes estão diretamente relacionadas com os termos e sua disposição na matriz. Sendo assim, preste bastante atenção em algumas das propriedades dos determinantes e nos exemplos a seguir.
1. Se todos os elementos de uma linha ou coluna forem iguais a zero (nulos), então o determinante da matriz também é nulo.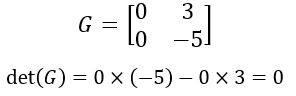
2. Se duas linhas ou duas colunas de uma matriz quadrada forem iguais, então seu determinante também será nulo.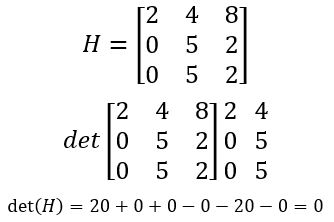
3. O determinante de uma matriz é igual ao determinante de sua transposta.
det(A) = det(AT)
4. Se uma matriz quadrada é invertível (possui inversa), o determinante da sua inversa é o inverso do seu determinante:
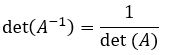
5. Se todos os elementos acima ou abaixo da diagonal principal de uma matriz quadrada forem iguais a zero (matriz triangular), o valor do determinante da matriz será somente o produto dos elementos da diagonal principal.
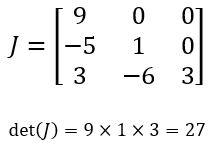
6. Analogamente à propriedade 5, o determinante de uma matriz identidade de qualquer ordem, será igual a 1.
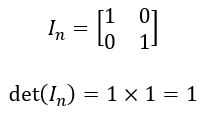
Viu como é importante levar em consideração essas propriedades facilitadoras dos cálculos? Não se preocupe, você não precisa decorar todas elas, apenas entender o porquê delas. Para isso, sugiro que pesquise sobre as demonstrações das propriedades acima.
Exercícios sobre determinantes
Para terminar seus estudos sobre esse tema, resolva os exercícios abaixo, selecionados pela nossa professora! Resolver exercícios é a melhor forma de fixar o conhecimento e, além disso, você já se acostuma com como o conteúdo é cobrado nas provas.
Questão 01)
O polinômio P(x) é definido através do determinante de uma matriz pela expressão:
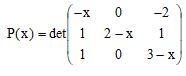
O mesmo polinômio pode ser também representado por
a) P(x) = (x + 2)(x – 2)(1 – x)
b) P(x) = –(x + 3)(x – 2)2
c) P(x) = –(x – 2)(x – 1)2
d) P(x) = (1 – x)(x – 2)2
Questão 02)
Sabendo que a e b são números reais, considere a matriz quadrada de ordem 3,
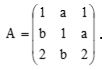
Se a soma dos elementos em cada linha da matriz A tem sempre o mesmo valor, então o determinante de A é igual a
a) 0.
b) 2.
c) 5.
d) 10.
Questão 03)
Seja A uma matriz quadrada de ordem 3, tal que cada elemento aij seja igual ao número binomial ![]() . O valor do determinante dessa matriz é:
. O valor do determinante dessa matriz é:
a) 0
b) 6
c) 5
d) 4
e) 10
Gabarito:
- D
- D
- D





