Círculo Trigonométrico: resumo com simulado de Matemática
O Círculo Trigonométrico é um recurso importante para você resolver questões básicas da matemática do Enem e dos vestibulares. Veja resumo com simulado e gabarito.
O Círculo Trigonométrico ajuda você a resolver questões básicas de matemática no Exame Nacional do Ensino Médio.
A origem de toda a trigonometria nasce ainda na Grécia Antiga, com o estudo das relações trigonométricas no Triângulo Retângulo. É a base de tudo.
As bases do Círculo Trigonométrico
Veja um resumo inicial do professor Sérgio Sarkis com os cálculos trigonométricos originais. Assim fica mais fácil para você compreender depois o Círculo Trigonométrico:
Os triângulos retângulos são polígonos de três lados e três vértices onde encontramos dois ângulos agudos e um ângulo reto (formando um ângulo de 90º).
Para facilitar a sua revisão, confira a descrição do resumo do professor Sarkis para você localizar o ponto certo de voltar à vídeo-aula:
00:00 a 00:35 – Apresentação do professor e vinheta de abertura.
00:36 a 2:39 – Esse triângulo se chama retângulo porque tem um ângulo reto (90º). O lado que estiver diante do ângulo reto será a hipotenusa. E os lados que formam o ângulo reto são chamados de catetos.
2:40 a 3:53 – Nesse exemplo, o professor traça uma reta que corresponde à altura relativa à hipotenusa. Confira a demonstração na lousa, na qual o prof também explica o que são projeções.
3:54 a 5:19 – Quando resolvemos problemas sobre triângulo retângulo, há dois tipos de fórmulas com as quais podemos trabalhar: a) relações trigonométricas (seno, cosseno, tangente), que veremos em outra aula. Você vai usá-las quando tiver as medidas dos ângulos internos // b) relações métricas serão usadas quando você trabalhar exclusivamente com lados e medidas de segmentos (não vai ter ângulo).
5:20 a 6:19 – De todas as relações métricas que existem, o Teorema de Pitágoras é o mais recorrentes nos vestibulares. Ele diz que o quadrado da hipotenusa deve ser igual à soma do quadrado dos catetos: hip² = cat² + cat². Além desse teorema, podemos destacar outras relações métricas que se você souber vão facilitar muito a resolução do exercício.
6:20 a 9:22 – Existe uma relação que diz que o produto dos catetos é sempre igual ao produto da hipotenusa pela altura: cat.cat = hip.alt. Outra relação: todo cateto ao quadrado é igual ao produto da sua projeção pela hipotenusa: cat² = proj.hip. Outra relação: o quadrado da altura é igual ao produto das suas projeções: alt² = proj.proj.
9:23 a 16:51 – Resolução de exercício.
Resumo sobre O Círculo Trigonométrico
Confira na aula gratuita os fundamentos que você precisa dominar sobre o Círculo Trigonométrico, com o professor Lucas Borguesan, do Curso Enem Gratuito.
Simulado Círculo Trigonométrico
Responda as dez questões e teste o seu nível para mandar bem na prova de verdade.
Sumário do Quiz
0 de 10 questões completadas
Perguntas:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
Information
.
Você já fez este questionário anteriormente. Portanto, não pode fazê-lo novamente.
Quiz is loading...
You must sign in or sign up to start the quiz.
Para iniciar este questionário, você precisa terminar, antes, este questionário:
Resultados
0 de 10 perguntas respondidas corretamente
Seu tempo:
Acabou o tempo
Você conseguiu 0 de 0 pontos possíveis (0)
| Pontuação média |
|
| Sua pontuação |
|
Categorias
- Sem categoria 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- Respondido
- Revisão
-
Pergunta 1 de 10
1. Pergunta
(UFRGS/2018)
Se a e b são ângulos agudos e complementares, o valor da expressão sen2(a + b) – cos2(a + b) é
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre círculo trigonométrico para acertar na hora da prova!
-
Pergunta 2 de 10
2. Pergunta
(ENEM/2018)
A rosa dos ventos é uma figura que representa oito sentidos, que dividem o círculo em partes iguais.
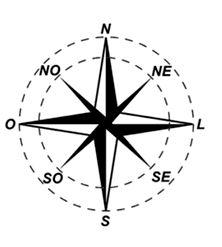
Uma câmera de vigilância está fixada no teto de um shopping e sua lente pode ser direcionada remotamente, através de um controlador, para qualquer sentido. A lente da câmera está apontada inicialmente no sentido Oeste e o seu controlador efetua três mudanças consecutivas, a saber:
- 1ª mudança: 135º no sentido anti-horário;
- 2ª mudança: 60º no sentido horário;
- 3ª mudança: 45º no sentido anti-horário.
Após a 3ª mudança, ele é orientado a reposicionar a câmera, com a menor amplitude possível, no sentido Noroeste (NO) devido a um movimento suspeito de um cliente.
Qual mudança de sentido o controlador deve efetuar para reposicionar a câmera?
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre círculo trigonométrico para acertar na hora da prova!
-
Pergunta 3 de 10
3. Pergunta
(ACAFE SC/2017)
A figura a seguir retrata a circunferência trigonométrica e as linhas pontilhadas indicam as projeções ortogonais das extremidades dos arcos de medida 30º, e 45º nos eixos coordenados do plano cartesiano. Escolhendo, ao acaso, um valor da tangente de um dos arcos indicados na figura (30º, e 45º), qual a probabilidade desse valor escolhido não ser igual ao seno ou cosseno de 30º, 45º ou 60º?
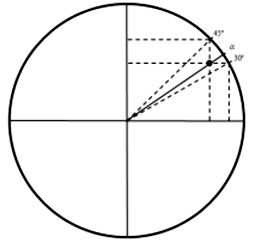 Correto
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre círculo trigonométrico para acertar na hora da prova!
-
Pergunta 4 de 10
4. Pergunta
(FUVEST SP/2015)
Diz-se que dois pontos da superfície terrestre são antípodas quando o segmento de reta que os une passa pelo centro da Terra.
Podem ser encontradas, e sites da internet, representações, como a reproduzida abaixo, em que as áreas escuras identificam os pontos da superfície terrestre que ficam, assim como os seus antípodas, sobre terra firme. Por exemplo, os pontos antípodas de parte do sul da América do Sul estão no leste da Ásia.
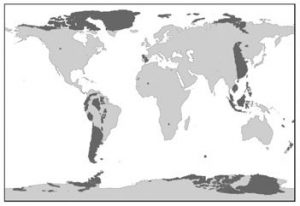
Se um ponto tem latitude x graus norte e longitude y graus leste, então seu antípoda tem latitude e longitude, respectivamente,
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre círculo trigonométrico para acertar na hora da prova!
-
Pergunta 5 de 10
5. Pergunta
(IFPE/2015)
Considere o arco
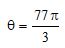 . É correto dizer que:Correto
. É correto dizer que:CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre círculo trigonométrico para acertar na hora da prova!
-
Pergunta 6 de 10
6. Pergunta
(UFRR/2015)
Conforme apresentado na figura, a seguir, por meio de um dispositivo, articularam-se dois discos, A (maior) e B (menor). O disco B gira dentro do disco A, e o raio de B é igual à metade da medida do raio de A; a seta coincide com o diâmetro do disco B, e indica um ângulo central.
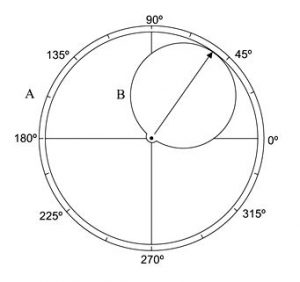
Os comprimentos dos segmentos determinados pelas interseções da borda do disco B com os eixos perpendiculares do disco A indicam os valores de quais funções trigonométricas?
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre círculo trigonométrico para acertar na hora da prova!
-
Pergunta 7 de 10
7. Pergunta
(UNIFAP AP/2015)
Agora é a vez de Ezequiel e Marta, que estudando trigonometria, lançam um desafio a seus colegas. O desafio é:
Qual o valor do cos45º – sen45º + cos135º.
Então os seus colegas para responderem ao desafio corretamente devem marcar qual alternativa:
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre círculo trigonométrico para acertar na hora da prova!
-
Pergunta 8 de 10
8. Pergunta
(UFJF MG/2015)
No processo de calcular o ângulo x formado entre duas avenidas transversais, um engenheiro obteve a seguinte equação sen x = sen3x. Sabendo que x não excede 180º, é CORRETO afirmar que:
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre círculo trigonométrico para acertar na hora da prova!
-
Pergunta 9 de 10
9. Pergunta
(UESB BA/2015)
O valor de
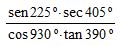 éCorreto
éCorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre círculo trigonométrico para acertar na hora da prova!
-
Pergunta 10 de 10
10. Pergunta
(FMJ SP/2014)
Sabe-se que uma matriz linha do tipo A = [x y] é a representação matricial de um ponto P(x, y) do plano cartesiano. A matriz
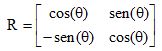 é chamada matriz de rotação, pois, quando AR = T, o ponto do plano que representa T é obtido a partir de uma rotação do ponto P de q graus no sentido trigonométrico (anti-horário). Seja T = [–1 2] resultado da rotação da matriz A = [2 1] em q graus no sentido anti-horário. Com base nas informações, é correto afirmar que o valor de θ, no intervalo [0º, 180º], que satisfaz tal rotação éCorreto
é chamada matriz de rotação, pois, quando AR = T, o ponto do plano que representa T é obtido a partir de uma rotação do ponto P de q graus no sentido trigonométrico (anti-horário). Seja T = [–1 2] resultado da rotação da matriz A = [2 1] em q graus no sentido anti-horário. Com base nas informações, é correto afirmar que o valor de θ, no intervalo [0º, 180º], que satisfaz tal rotação éCorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre círculo trigonométrico para acertar na hora da prova!
Sobre o(a) autor(a):
Ana Cristina Peron -
Gostou? Compartilhe!
Continue lendo:
Aqui vão 2 publicações relacionadas que talvez você goste:

Como resolver a prova de Matemática no Enem 2024? Veja as dicas do professor
Por Melina Zanotto | 08 de novembro
Confira as orientações e estratégias do professor Lucas Borguezan para se sair bem na prova de Matemática no Enem 2024.

Aulão Enem de Matemática: revisão intensiva e gratuita para a prova
Por João Vianney dos Valles Santos | 11 de outubro
Assista ao Aulão Enem de Matemática do Curso Enem Gratuito e revise os conteúdos mais importantes para a prova.


