O que é Binômio de Newton e quais suas propriedades
Revise os números binomiais e o Binômio de Newton. Estude Matemática com o Curso Enem Gratuito!
Neste post você vai aprender sobre o binômio de Newton e também sobre os números binomiais e suas propriedades, além de conhecer a fórmula do termo geral de um Binômio de Newton.
Antes de iniciarmos nossa revisão sobre o Binômio de Newton, é preciso que você relembre alguns conceitos relevantes para o entendimento desta aula. Vamos lá?
- Binômio: Um binômio é uma expressão algébrica com dois termos algébricos ou um termo algébrico e outro numérico.
- Termo algébrico: Quando nos referimos a termo algébrico, estamos falando de um termo que tenha letras (incógnitas).
Binômio de Newton
O Binômio de Newton é um binômio elevado a uma potência qualquer. E é claro que recebeu esse nome por ser descoberto por de Isaac Newton. Podemos dizer que o Binômio de Newton é uma potência da forma:
Podemos dizer que o Binômio de Newton é uma potência da forma: (x + y)n
Onde x e y pertencem ao conjunto dos números reais e n pertence ao número.
Como em qualquer potência, o binômio é a base da potência e é resolvido a partir do expoente. O expoente indica quantas vezes esse binômio deve ser multiplicado por ele mesmo. Observe o exemplo abaixo:

Temos alguns casos em que os binômios deverão ser elevados a expoentes muito grandes e aí vem a calhar uma ferramenta que facilite as nossas vidas, não é mesmo? Essa ferramenta se chama número binomial.
Número binomial
Um número binomial é um número escrito na seguinte forma:

Os números n e p são números naturais e n deve ser maior ou igual a p, de tal forma que sua fórmula vem da
Análise Combinatória
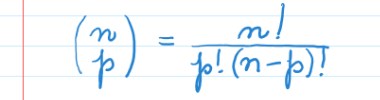
Podemos dizer que um número binomial é o mesmo que uma combinação simples:
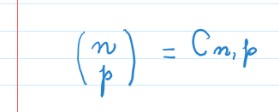
Ou seja:
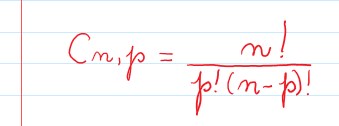 Propriedades dos números binomiais
Propriedades dos números binomiais
Esses números binomiais obedecem a duas propriedades, que necessitamos saber:
1ª propriedade: Dois números binomiais são iguais se tiverem o mesmo denominador e suas classes forem iguais.
Exemplo:
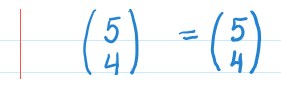
2ª propriedade: Dois números binomiais são iguais se tiverem o mesmo denominador e a soma de suas classes for igual a seu numerador.
Exemplo:
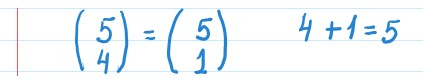
A soma das classes é denominada de Binomiais Complementares ou Combinações Complementares.
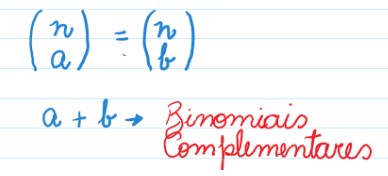
Lei de formação do Binômio de Newton
Agora que já sabemos o que são números binomiais, iremos entender como eles nos ajudarão no cálculo de potências com bases binomiais e expoentes grandes.
Para isso, apresentaremos a você a lei de formação do Binômio de Newton:
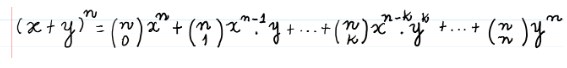
Os números x e y são números Reais e o expoente n é um número natural.
Observe que os expoentes de:
x são decrescentes e decrescem de 1 em 1 unidade até chegar a zero.
y são crescentes e iniciam do zero e crescem de 1 em 1 unidade até chegar ao valor de n.
Exercícios resolvidos com o Binômio de Newton
Agora que você já aprendeu a teoria, vamos ver alguns exemplos para aprender a aplicá-la.
1. Desenvolva a seguinte potência:![]()
Solução:
Para resolvermos essa potência, colocaremos a fórmula geral acima. Assim, saberemos quem é o primeiro termo o segundo termo do binômio e que serão os numeradores e as classes dos números binomiais:
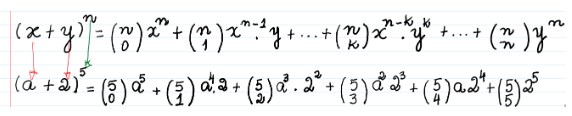
Precisamos agora calcular os valores de cada número binomial pela fórmula:
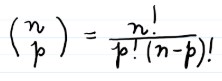
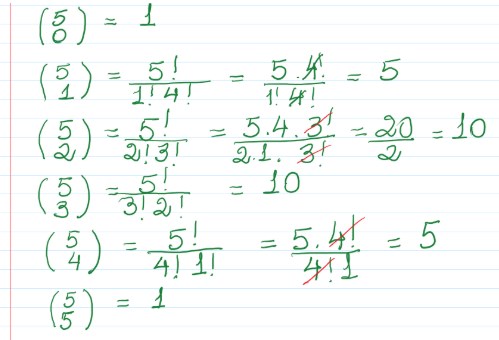
Calculamos cada um dos números binomiais e agora vamos substitui-los por seus valores:
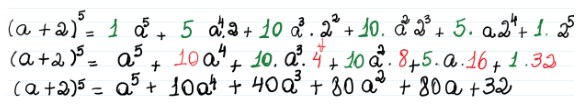
Substituímos os números binomiais por seus valores na cor verde, resolvemos as potências e as escrevemos na cor vermelha para que fique melhor de acompanhar. Na terceira linha temos o resultado do binômio.
Termo Geral do Binômio de Newton
Agora que já exemplificamos como calcular um Binômio pela lei de formação do Binômio de Newton iremos apresentar o Termo Geral do Binômio de Newton.
O Termo Geral do Binômio de Newton foi retirado da própria lei de formação do Binômio de Newton:
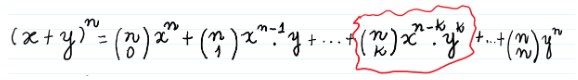
O termo geral é o que está circulado em vermelho, ou seja:
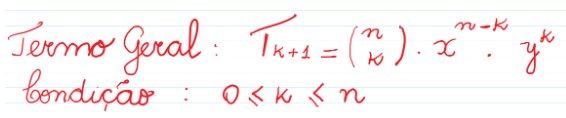
Com essa pequena fórmula podemos calcular qualquer termo de um binômio elevado a uma potência n. Veja outro exemplo:
2. Complete a frase: _____________________é o 4º termo de ![]()
A alternativa que contém o valor que completa a frase acima é:
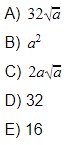
Resolução:
Temos duas maneiras de resolver essa questão: a primeira é ir resolvendo por multiplicação de polinômio por polinômio. Uma solução bem extensa e bem trabalhosa. A segunda forma é usando a fórmula do termo geral do Binômio de Newton.
Veja que:
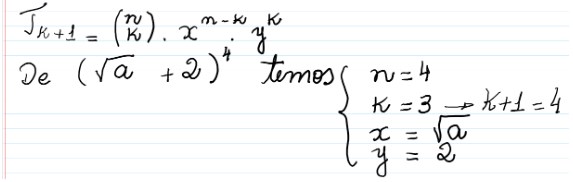
Agora vamos substituir os valores na fórmula e resolver:
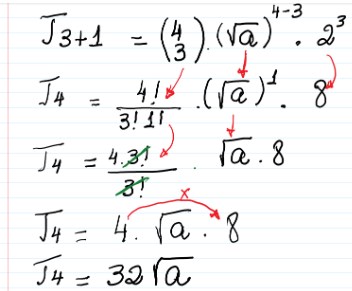
A alternativa correta é a A.
( Fonte: Matsubara, Juliane B. et all. Conexão com a Matemática V2. São Paulo: Ed. Moderna, 2010)
Referências Bibliográficas:
DANTE, Luiz R. Matemática & Aplicações v.2. São Paulo: Ed. Ática, 2013.
BALESTRI, Rodrigo. Matemática: Interação e Tecnologia v2. São Paulo: Leya, 2016.
Matsubara, Juliane B. [et all.]. Conexões com a Matemática v2. São Paulo: Moderna, 2010.
Videoaula
E aí? Conseguiu revisar o conteúdo? Beleza! Agora, para fixar o conteúdo, veja a aula do nosso canal no youtube, com o professor de Matemática Sérgio Sarkis:
Exercícios sobre o Binômio de Newton
Sumário do Quiz
0 de 10 questões completadas
Perguntas:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
Information
.
Você já fez este questionário anteriormente. Portanto, não pode fazê-lo novamente.
Quiz is loading...
You must sign in or sign up to start the quiz.
Para iniciar este questionário, você precisa terminar, antes, este questionário:
Resultados
0 de 10 perguntas respondidas corretamente
Seu tempo:
Acabou o tempo
Você conseguiu 0 de 0 pontos possíveis (0)
| Pontuação média |
|
| Sua pontuação |
|
Categorias
- Sem categoria 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- Respondido
- Revisão
-
Pergunta 1 de 10
1. Pergunta
(Mackenzie SP / 2017)
O número de valores de x, para os quais os coeficientes binomiais
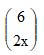 e
e 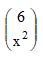 sejam iguais, éCorreto
sejam iguais, éCorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre binômio de Newton para acertar na hora da prova!
-
Pergunta 2 de 10
2. Pergunta
(FGV / 2017)
Desenvolvendo-se a expressão (x + 2)10, obtemos um polinômio
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre binômio de Newton para acertar na hora da prova!
-
Pergunta 3 de 10
3. Pergunta
(IME RJ/ 2016)
O valor da soma abaixo é:
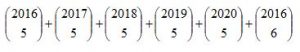 Correto
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre binômio de Newton para acertar na hora da prova!
-
Pergunta 4 de 10
4. Pergunta
(UERN / 2015)
Considere a seguinte equação:
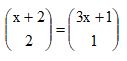
A partir dessa equação, conclui-se que o número binomial
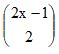 equivale aCorreto
equivale aCorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre binômio de Newton para acertar na hora da prova!
-
Pergunta 5 de 10
5. Pergunta
(UNITAU SP/ 2015)
O valor do número binomial
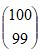 éCorreto
éCorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre binômio de Newton para acertar na hora da prova!
-
Pergunta 6 de 10
6. Pergunta
(ESPM SP/ 2014)
Os binomiais
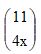 e
e 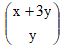 são complementares e, por isso, são iguais. Seu valor é:Correto
são complementares e, por isso, são iguais. Seu valor é:CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre binômio de Newton para acertar na hora da prova!
-
Pergunta 7 de 10
7. Pergunta
(ESPM SP / 2014)
Simplificando-se a expressão com números binomiais
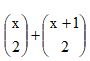 , para x ≤ 0, obtém-se:Correto
, para x ≤ 0, obtém-se:CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre binômio de Newton para acertar na hora da prova!
-
Pergunta 8 de 10
8. Pergunta
(UESPI/ 2014)
O coeficiente de x3no desenvolvimento binomial de (x + 3)5é:
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre binômio de Newton para acertar na hora da prova!
-
Pergunta 9 de 10
9. Pergunta
(UNITAU SP/ 2014)
O coeficiente de x5 no polinômio P(x) = (x + 3)8 é:
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre binômio de Newton para acertar na hora da prova!
-
Pergunta 10 de 10
10. Pergunta
(UNITAU SP/ 2014)
O coeficiente de y6 no polinômio P(y) = (3 – y)9 é
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre binômio de Newton para acertar na hora da prova!

Sobre o(a) autor(a):
Wania Maria de A. Pereira - A professora Wania Maria de A. Pereira é graduada em Física e Matemática pela Universidade Federal de Santa Maria (UFSM) e é Psicopedagoga com enfoque em Gestão de Pessoas (UNC) e especialista em Educação a Distância (SENAC- SC). Atuou na rede particular, estadual e municipal por 26 anos no Estado de Santa Catarina. Autora de diversos materiais didáticos para universidades públicas e privadas na área de Matemática, Metodologia de Ensino de Matemática e Psicopedagogia. Atualmente trabalha na área de Projetos de Tecnologias Digitais de Informação e Comunicação (TDICs). LinkedIn: https://www.linkedin.com/in/wmariaap/.
Gostou? Compartilhe!
Continue lendo:
Aqui vão 2 publicações relacionadas que talvez você goste:

Como resolver a prova de Matemática no Enem 2024? Veja as dicas do professor
Por Melina Zanotto | 08 de novembro
Confira as orientações e estratégias do professor Lucas Borguezan para se sair bem na prova de Matemática no Enem 2024.

Aulão Enem de Matemática: revisão intensiva e gratuita para a prova
Por João Vianney dos Valles Santos | 11 de outubro
Assista ao Aulão Enem de Matemática do Curso Enem Gratuito e revise os conteúdos mais importantes para a prova.


