A circunferência é o conjunto de todos os pontos equidistantes (mesma distância) de um ponto de referência.
A circunferência e o círculo são tão importantes quanto os polígonos na geometria plana. Na aula de hoje você vai aprender sobre circunferência, sua definição, seus elementos e seu perímetro.
Características do Círculo e da Circunferência – Logo de início as pessoas se confundem, e isso é muito normal. Uma dica bem básica é que o Círculo tem uma área interna definida a ser considerada, enquanto a circunferência tem a ver apenas com o anel, com o traço que forma a circunferência. Veja:
Também, vamos aprender sobre o círculo, sua definição, seus elementos, o cálculo de áreas e de comprimentos de arco.
Circunferência
Dizemos que uma circunferência é o conjunto de todos os pontos equidistantes (mesma distância) de um ponto de referência. A essa distância damos o nome de raio da circunferência (denotado por r) e ao ponto de referência damos o nome de centro da circunferência.
Observe abaixo.

Perceba pela definição acima que a circunferência é apenas a borda. Ou seja, quando falamos de circunferência nos referimos apenas ao “caminho redondo” da imagem acima, sem considerarmos o seu interior.
Elementos da circunferência
O centro e o raio são dois personagens essenciais quando falamos de circunferências. Mas, além deles, precisamos mencionar outros elementos:
- Corda: qualquer segmento de reta cujas extremidades são 2 pontos distintos da circunferência;
- Diâmetro: é a corda da circunferência que passa pelo centro dela;
- Flecha: segmento de reta com uma extremidade em um ponto da circunferência e outra extremidade em um ponto de uma corda, sendo perpendicular à corda;
- Arco: é a porção da circunferência compreendida entre dois pontos dela.
Aqui vale ressaltar o seguinte:
- O raio pode ser definido como sendo qualquer segmento de reta cujas extremidades são o centro e um ponto qualquer da circunferência;
- O diâmetro possui medida igual ao dobro da medida do raio;
- O diâmetro é a maior corda da circunferência;
- Existem 2 notações para o arco da circunferência. Suponha, com o auxílio da imagem acima o arco compreendido entre os pontos A e B. Para este arco utilizamos a notação

- A notação mais correta para medida de arco é
 mas vamos tratar
mas vamos tratar  como sinônimo de arco(AB) por questão de praticidade.
como sinônimo de arco(AB) por questão de praticidade.
Veja na imagem abaixo os seus elementos.

Da figura temos o seguinte:
- OA = raio;
- BF = diâmetro;
- CE = corda;
- DG = flecha;
- Arco(AB), arco(BC), arco(CD), arco(DE), arco(EF), arco(FA) representados.
Além dos elementos, existe um cálculo de extrema importância a respeito da circunferência: o cálculo do comprimento (ou perímetro – notação: 2p).
Cálculo do comprimento da circunferência
O comprimento é calculado através da seguinte expressão:
C = 2 . π . r
Com r sendo o raio da circunferência.
Este comprimento nada mais é do que a medida da “borda” da imagem, se essa borda pudesse “se abrir e virar um segmento de reta”. Você provavelmente já ouviu falar desse assunto alguma vez na sua vida, não é mesmo?
A partir do comprimento da circunferência somos capazes de encontrar o comprimento de um arco de circunferência, da seguinte forma:

360° – 2π . r
Ô – l
Para isso, precisamos saber o valor de r e de Ô.
Se o ângulo Ô for medido em radianos, a regra de três se torna:
2π – 2π . r
Ô – l
Para entender ainda melhor como calcular os cálculos da circunferência, confira este resumo do professor Lucas Borguezan:
Agora que já estudamos sobre a circunferência, não podemos esquecer do círculo, então vamos começar a estudá-lo agora.
Círculo
Considere uma circunferência de centro O e raio r. Dizemos que o círculo é o conjunto de todos os pontos cuja distância entre estes pontos e o ponto O seja menor ou igual a r.

Perceba então que na definição do círculo consideramos tanto a “borda” (circunferência) quanto o “interior da imagem” com a condição da distância ser menor ou igual a r.
Essa é a diferença entre as definições de circunferência e círculo.
Existe ainda uma outra forma de definir o círculo, que é a seguinte: círculo é a região delimitada por uma circunferência. Perceba que o centro e o raio da circunferência coincidem com o centro e o raio do círculo.
Assim como a circunferência possui seus elementos, os círculos também os têm. Ainda, da mesma forma que conseguimos calcular o comprimento da circunferência, no círculo conseguimos calcular a sua área e a área dos seus elementos.
Elementos do círculo
Os elementos do círculo são:
- Centro;
- Raio;
- Diâmetro;
- Setor circular: porção do círculo delimitada por um arco de circunferência e raios cuja extremidades são o centro e os pontos extremos do arco;
- Segmento circular: porção do círculo delimitada por uma corda e por um arco de circunferência que possuem os mesmos pontos extremos;
- Coroa circular: considere dois círculos que possuem o mesmo centro. A coroa circular é a região compreendida entre o interior do círculo de maior raio e o exterior do círculo de menor raio.
Veja abaixo a representação destes elementos:

Agora que já sabemos os elementos do círculo, vamos dar uma olhada nos cálculos de suas áreas.
Área do Círculo

A área de um círculo pode ser calculada através de:
S = π . r²
Em que r é o raio do círculo.
Área do Setor Circular
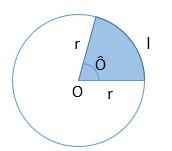
A área do setor circular pode ser calcula de duas formas, ambas se utilizando de regra de três:
- Conhecendo o valor do ângulo Ô:
360° — πr²
Ô — Ssetor
Aqui, lembre-se de prestar atenção se o ângulo Ô foi dado em graus ou em radianos e faça a adaptação necessária na regra de três.
- Conhecendo o valor do arco l que o delimita:
2πr — πr²
l — Ssetor
Área do Segmento Circular

A área do segmento circular é calculada através de:
Ssegmento = Ssetor – Striângulo
Área da Coroa Circular

A área da coroa circular é calculada através de:
Scoroa = Scírculo de maior raio – Scírculo de menor raio
Para aprofundar seus estudos, veja mais esta videoaula com a parte 2 sobre os ângulos na Circunferência.
Exercícios resolvidos
Pronto, agora você já sabe calcular comprimento de circunferência, área do círculo e dos seus elementos. Agora, veja os exemplos abaixo para dar uma esclarecida de como resolver os cálculos.
- (Exemplo criado pela autora) Considere a imagem abaixo.

Perceba que temos dois círculos, um de raio 10 cm e outro de raio 8 cm, delimitados por suas respectivas circunferências. Ainda, como os círculos são concêntricos, estamos diante, também, de uma coroa circular.
Vamos calcular o comprimento da circunferência que delimita o círculo de raio 10cm, a área do círculo de raio 8cm e a área da coroa circular:
Comprimento da circunferência de raio 10 cm:
2 . π . r = 2 . π . 10 cm = 20πcm
Área da circunferência de raio 8 cm:
S = π . r² = π . (8)² cm = 64πcm²
Área da coroa circular:
S = Scírculo maior – Scírculo menor
S = π . (10)² – π . (8)²
S = 100π – 64π
S = 36π cm²
-
(Exemplo criado pelo autor) Considere agora a imagem abaixo.

Vamos encontrar o comprimento do arco l, a área do setor circular e a área do segmento circular.
Comprimento do arco l:
360° – 2π . r
Ô – l
Dados os valores do exemplo temos:
360º – 2π . 10
60º – l
Resolvendo temos:
360º . l = 2π . 10 . 60º
l = 23π ÷ 6
Área do setor circular:
Vamos usar a regra de três que utiliza o valor do ângulo conhecido:
360º – πr²
Ô – Ssetor
Dados os valores do exemplo temos:
360º – π . (10)²
60º – Ssetor
Assim temos:
360º . Ssetor = 60º . π . 100
Ssetor = 50π ÷ 3
Área do segmento circular:

Percebeu que os números ficaram feios? Isso pode depender de exercício pra exercício, de acordo com as aproximações que a questão der ou não a respeito de valores como π e √3.
Exercícios
Questão 01 – (FATEC SP/2020)
A utilização de cadeira de rodas impõe limites à execução de tarefas por dificultar a aproximação aos objetos e o alcance a elementos acima e abaixo do raio de ação de uma pessoa sentada. A dificuldade nas manobras com a cadeira de rodas pressupõe o estabelecimento de um raio mínimo para a execução de atividades. As figuras se baseiam nas recomendações da Associação Brasileira de Normas Técnicas (ABNT) para manobras de rotação.

De acordo com as dimensões apresentadas nas figuras, para que uma pessoa em cadeira de rodas possa efetuar uma manobra de 360º, ela precisa de um espaço mínimo equivalente a um círculo, centrado no eixo de rotação da cadeira, de raio igual a
a) 0,60.
b) 0,75.
c) 0,85.
d) 1,20.
e) 1,50.
Gab: B
Questão 02 – (UniNorte AM/2019)
A figura representa o esboço do caminho percorrido por uma pessoa para se deslocar do ponto P até o ponto R.

Sabe-se que
- a curva PQ é um arco de circunferência de raio 1,6km.
- o segmento QR representa um trecho retilíneo do caminho, medindo 2,8km.
Se, em determinado dia, o percurso PR foi feito de automóvel em 6 minutos, pode-se afirmar, considerando π = 3, que a velocidade média desenvolvida pelo automóvel foi de
a) 40km/h
b) 38km/h
c) 36km/h
d) 32km/h
e) 30km/h
Gab: A
Questão 03 – (IFGO/2019)
Se o raio R de uma circunferência for reduzido pela metade, é correto afirmar que:
a) o valor da área círculo ficará reduzido pela metade do valor da área do círculo inicial de raio R.
b) o valor da área do círculo ficará reduzido a ¾ do valor da área do círculo inicial de raio R.
c) o comprimento da circunferência se reduzirá a ¼ do valor do comprimento da circunferência inicial de raio R.
d) o comprimento da circunferência se reduzirá a metade do valor do comprimento da circunferência inicial de raio R.
Gab: D

