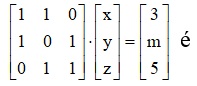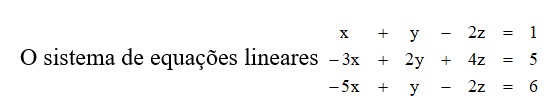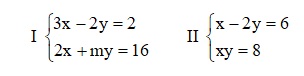Equações e sistemas lineares: matemática básica
Estude as equações, os sistemas lineares e suas soluções. Ao final, resolva a lista de exercícios para testar seus conhecimentos! São 10 questões e o gabarito sai na hora!
Para tudo se tem uma solução nesse mundo, não é verdade? Para responder essa pergunta, confira esse post. Aqui estudaremos as equações lineares, os sistemas lineares e suas soluções.
Qual será o valor de x e y sabendo que a soma de ambos é igual a 10 e que a diferença é entre eles é 4? Essa situação e muitas outras do nosso cotidiano são modeladas por equações matemáticas, algumas chamadas de equações lineares.
Introdução à resolução de Sistemas
Você sabia que um conjunto de equações lineares forma um sistema linear? Veja na aula de introdução com o professor Lucas Borguezan, do canal do Curso Enem Gratuito.
Depois desta introdução com o professor Lucas você vai aprender mais rápido o conceito de equações e sistemas lineares, suas aplicações, suas classificações e seus métodos de resolução. Bora revisar esse conteúdo?
Equações lineares – o termo independente e a variável
As equações lineares são as da seguinte forma:
Os coeficientes são: 2, -9 e 5.
As variáveis são: x, y e z.
O número 1 é o termo independente.
Classificação das equações lineares
Você sabia que podemos classificar uma equação linear? É o que veremos a seguir.
Quando temos uma equação linear cujo termo independente é igual à zero, dizemos que essa equação é homogênea, ou seja,
![]()
Não se esqueça, para dizer se uma equação é ou não homogênea basta analisar o coeficiente . Vamos treinar um pouquinho?
Exemplo 01: Classifique se as equações são homogêneas.
a) x + y + 9z = 3
R: Como , o que é diferente de zero, temos que a equação não é homogênea.
b) -8x + y -6 = 0
![]()
Sabe o que é interessante também estudar sobre as equações? A solução delas. O conjunto de pontos que é solução de uma equação linear é chamado de conjunto solução.
Conjunto solução – determinando a solução de uma equação linear
Um conjunto de pontos é solução de uma equação linear se ao substituirmos os pontos na equação à igualdade se torna verdadeira.
Exemplo 02: Veja se o conjunto (0, 1, 2) é solução da equação x-2y+z=0.
Solução: Vamos substituir os pontos na equação, sempre lembrando que o primeiro valor corresponde a variável x, o segundo a variável y e o terceiro a variável z, assim temos:
(0)-2(1)+(2)=0
0-2+2=0
0=0
Observe que valor encontrado na 1º membro da equação é igual ao valor do 2º membro da equação, ou seja, é válida a igualdade. Quando ocorre isso, dizemos que o conjunto (0, 1, 2) é o conjunto solução da equação. Veja uma situação em que os pontos dados não é o conjunto solução.
Exemplo 03: Verifique se (-2, 6, 0) é solução da equação anterior.
Solução: Substituindo os pontos dados na equação obtemos:
(-2)-2(6)+0=0
-2-12+0=0
-14 ≠0
Como o valor encontrado do lado esquerdo é diferente do encontrado no lado direito, temos que (-2, 6, 0) não é conjunto solução da equação. Agora você sabia que quando temos mais que uma equação linear, chamamos esse conjunto de equações lineares de sistemas lineares?
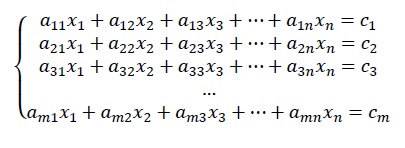
Publicado em 02 de junho de 2014, retirado em: https://www.stoodi.com.br/blog/2014/06/02/sistemas-lineares-o-que-sao-e-como-resolve-los/
Sistemas lineares – o conjunto de equações lineares
Um sistema linear é um conjunto de equações lineares. Podemos ter sistemas com 2 equações e 2 variáveis ou com 2 equações e 3 variáveis, ou ainda, com 3 equações e 3 variáveis. Na verdade, devemos ficar atentos à quantidade de equações e a quantidade de variáveis, pois esses números determinaram vários aspectos sobre um sistema. Mas isso veremos brevemente. Então dizemos que um sistema linear é um conjunto de equações lineares de m equações e n variáveis. São exemplos:

Sistema linear de 2 equações e 3 variáveis.
Um sistema linear pode ser representado em forma de uma matriz. Veja como fazer.
Utilizando o sistema do exemplo 06, podemos escrever o sistema na forma a seguir.

A forma apresentada chama-se de forma matricial. Note que a 1º coluna são todos os valores acompanhados de x em todas as equações, a 2º coluna são todos os valores que acompanham y em todas as equações e a 3º coluna são todos os valores que acompanham z em todas as equações.
Podemos classificar os sistemas lineares de acordo com o número de soluções encontradas, e é o que abordaremos a seguir.
Classificando os sistemas lineares de acordo com a quantidade de soluções
Os sistemas lineares são classificados de acordo com a quantidade de soluções encontradas do mesmo. São as classificações:
Sistema possível e determinado (SPD): é quando o sistema possui uma única solução. O sistema abaixo possui uma única solução, que é dada pelo par (2, 3).
![]()
Logo, esse sistema é possível e determinado.
Sistema Possível e Indeterminado (SPI): é quando o sistema possui infinitas soluções, ou seja, x e y podem assumir vários valores. Veja um exemplo abaixo.
![]()
Note que o par ordenado (0,1) é solução do sistema. Assim como (4, 0) também é solução. Portanto, esse sistema é possível e indeterminado.
Sistema Impossível (SI): é um sistema que não possui solução, ou seja, não conseguimos encontrar valores as incógnitas.
![]()
O sistema acima não possui solução, por isso o chamamos de sistema impossível. Também há outra forma de classificarmos um sistema, mas para isso deve coloca-lo na forma matricial.
Classificando os sistemas lineares de acordo com o determinante
Como já mostramos anteriormente, um sistema linear pode ser apresentado na forma matricial. Feito isso, basta calcularmos o determinante da matriz. De acordo com o determinando, classificamos o sistema em:
Sistema possível e determinado: é quando o determinante da matriz é diferente de zero.
Sistema possível e indeterminado e sistema impossível: é quando o determinante da matriz é igual à zero. Quando acontecer esse caso, devemos classificar em SPI ou SI verificando se o sistema tem solução ou não.
Vamos resolver o próximo exercício juntos? Se liga nesse exercício, pois ele caiu no Enem!
Exemplo 07: (UEL) O sistema abaixo, de incógnitas x e y, é:
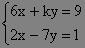
a) impossível, para todo k real diferente de -21;
b) possível e indeterminado, para todo k real diferente de -63;
c) possível e determinado, para todo k real diferente de -21;
d) possível e indeterminado, para todo k real diferente de -3;
e) possível e determinado, para todo k real diferente de -1 e -63.
Solução: Devemos determinar a solução do sistema inicialmente. Para isso, vamos multiplicar a equação 02 por -3, ou seja,
-3( 2x-7y=1)
-6x+21y=3
Somaremos a equação obtida com a equação 01.
6x+ky=9
+ -6x+21y=3
Logo, temos como resultado a equação ky+21y=12. Isolando y temos:
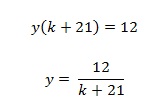
Já a segunda afirmação também é falsa, pois se k = -21 o sistema não possui solução. Logo, não será para todo k ≠ -63 que o sistema será possível e indeterminado. O mesmo argumento podemos utilizar para justificar que as afirmações das letras (d) e (e) são falsas. Portanto, a afirmação ( c ) está correta, pois para todo k ≠ -21 o sistema será possível e determinado. Resposta: letra (c).
Para fixar seus estudos sobre equações lineares, confira a aula abaixo, disponível no nosso canal:
Exercícios sobre Sistemas Lineares:
.