Função modular e módulo: Simulado e resumo de Matemática
Confira um resumo com a Introdução à Função Modular e Módulo. Veja os exercícios resolvidos e depois teste o seu nível no Simulado de Matemática:
Dica básica para entender Módulo, Função Modular, e gabaritar o Simulado: Você já deve ter reparado que toda a vez que você resolve uma equação e o enunciado se trata de uma medida de comprimento, o resultado que você obtém precisa ser positivo.
Além disso, em casos em que temos dois resultados, como em uma fórmula de Bhaskara, ao se tratar de distâncias “escolhemos” apenas o resultado positivo. Você sabe por que isso acontece?
Simplesmente porque uma distância nunca pode ser negativa. Imagine você andando por 300 metros: existe a possibilidade de andar 300 metros negativos? É para expressar esse conceito de distância negativa que surgiram o módulo e a função modular.
Introdução à Função Modular e Módulo
Confira agora com o professor Lucas, que é do time de feras do canal do Curso Enem Gratuito:
Muito bom e detalhado este resumo inicial do professor Lucas. Vale a pena ver de novo!
Entenda o que é o Módulo
Módulo
O módulo de um número real surgiu da necessidade de medir a distância de um número negativo até o zero. Mas, na verdade, a definição do módulo é que expressa o conceito de distância. Matematicamente falando, o módulo é a distância de um determinado número da reta real (independente se for negativo ou positivo) até o zero. Sendo assim, o módulo de um número real sempre será positivo, pois a distância sempre será positiva.
Como um exemplo, a distância de – 3 até o 0 é 3 u.c.:
Então:
|- 3 | = 3
Da mesma forma, a distância de 5 até 0 é 5 u.c.
Então:
| 5 | = 5
Por definição, podemos dizer que:
|x| = x, se x ≥ 0 (positivo)
-x, se x < 0 (negativo)
Para entendermos melhor, vamos ver exemplos:
Exemplos de módulo:
Calcule o valor de x na equação |2x – 1| = 9
Para que os dois lados da equação sejam equivalentes, significa que o que está dentro do módulo deve ser igual a 9 ou igual a – 9.
Dessa forma: 2x – 1 = 9 ou 2x – 1 = – 9
Assim 2x = 9 + 1 2x = – 9 +1
Portanto 2x = 10 2x = – 8
x = 5 x = -4
Isso quer dizer que tanto para x = 5 quanto para x = – 4, a equação |2x – 1| = 9 é verdadeira. O conjunto solução se apresenta da forma:
S = { -4, 5 }
Exemplo 2:
Quais são as possíveis soluções da equação | 5x-6 | = x² ?
Segundo a definição: temos que 5x – 6 = x² ou 5x-6 = -x². Resolvendo cada uma das equações:
f5x – 6 = x²
x² – 5x + 6 = 0
S = -5 , P = 6
(x-2)(x-3) = 0
x = 2 ou x = 3
5x – 6 = -x²
x² + 5x – 6 = 0
S = 5, P = -6
(x+6)(x-1) = 0
x = -6 ou x = 1
Assim, teremos quatro soluções, S = { – 6 , 1, 2, 3 }
Simulado de Função Modular e Módulo
Sumário do Quiz
0 de 10 questões completadas
Perguntas:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
Information
.
Você já fez este questionário anteriormente. Portanto, não pode fazê-lo novamente.
Quiz is loading...
You must sign in or sign up to start the quiz.
Para iniciar este questionário, você precisa terminar, antes, este questionário:
Resultados
0 de 10 perguntas respondidas corretamente
Seu tempo:
Acabou o tempo
Você conseguiu 0 de 0 pontos possíveis (0)
| Pontuação média |
|
| Sua pontuação |
|
Categorias
- Sem categoria 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- Respondido
- Revisão
-
Pergunta 1 de 10
1. Pergunta
(UEG GO/2016)
Na figura a seguir, é apresentado o gráfico de uma função f, de R em R
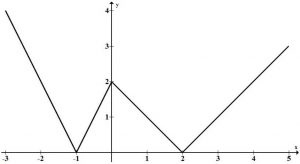
A função f é dada por
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre função modular para acertar na hora da prova!
-
Pergunta 2 de 10
2. Pergunta
(UNIFAP AP/2015)
Ezequiel e Marta têm dificuldades para resolver problemas que envolvam funções modulares. Daí escolhem a seguinte questão para treinar:
Sendo f(x) = |2x + 1|, qual é o valor de x quando f(x) = 2.
Desta forma, qual foi à solução correta que eles encontraram:
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre função modular para acertar na hora da prova!
-
Pergunta 3 de 10
3. Pergunta
(UFTM/2010)
A função f(x) = |x + 3| – |x + 1| tem valor maior que zero, para x real obedecendo à condição
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre função modular para acertar na hora da prova!
-
Pergunta 4 de 10
4. Pergunta
(UECE/2009)
Em um referencial cartesiano ortogonal, no qual a unidade linear é o centímetro, a área da região limitada pelo gráfico da equação |x| +|y| = 1, em centímetros quadrados, é
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre função modular para acertar na hora da prova!
-
Pergunta 5 de 10
5. Pergunta
(UESC BA/2009)
Sobre o conjunto-solução da equação |x + 2| – |2x – 1| = -1, em x ∈ R, tem-se que é um conjunto
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre função modular para acertar na hora da prova!
-
Pergunta 6 de 10
6. Pergunta
(UFAC/2009)
Os números reais x que satisfazem a desigualdade
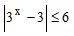 formam um conjunto que:Correto
formam um conjunto que:CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre função modular para acertar na hora da prova!
-
Pergunta 7 de 10
7. Pergunta
(IBMEC SP Insper/2008)
O gráfico que melhor representa a função real f(x) = 2 – |1 – x| é:
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre função modular para acertar na hora da prova!
-
Pergunta 8 de 10
8. Pergunta
(UFU MG/2018)
Considere a função definida por y = f (x) = k . |x – 3| , em que k é um número natural constante, x uma variável assumindo valores reais e |a| representa o módulo do número real a. Representando, no sistema de coordenadas cartesianas, o gráfico de y = f(x), tem-se que esse gráfico e os eixos coordenados delimitam um triângulo de área igual a 72cm2.
Nas condições apresentadas, o valor de k, em cm, é um número
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre função modular para acertar na hora da prova!
-
Pergunta 9 de 10
9. Pergunta
(ESPCEX/2018)
Sabendo que o gráfico a seguir representa a função real f(x) = |x – 2| + |x + 3|, então o valor de a + b + c é igual a
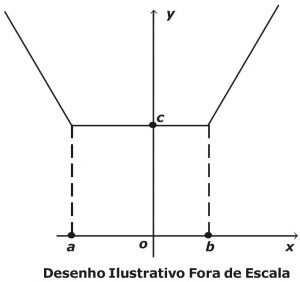 Correto
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre função modular para acertar na hora da prova!
-
Pergunta 10 de 10
10. Pergunta
(Fac. Israelita de C. da Saúde Albert Einstein SP/2017)
A função modular f(x) = |ax + b|, a ∈ IR*, b ∈ IR* e a função quadrática g(x) = –0,5x2 + 2x + 6 têm dois pontos em comum, conforme o gráfico.
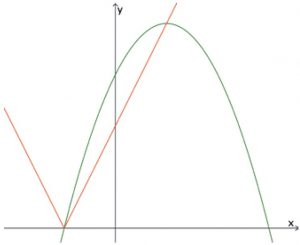
Um desses pontos corresponde à menor raiz da função g e o outro ponto corresponde ao maior valor dessa função. O produto ab vale
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre função modular para acertar na hora da prova!
.
Como foi o seu resultado no Simulado de Função Modular e Módulo? Acertou quantas questões de Função Modular?
Parece complicado, mas dá sim pra mandar bem. Se você não acertou pelo menos sete questões, é hora de mergulhar mais fundo. Veja um resumo completo sobre Função Modular e Módulo.

Sobre o(a) autor(a):
Ana Cristina Peron -
Gostou? Compartilhe!
Continue lendo:
Aqui vão 2 publicações relacionadas que talvez você goste:

Como resolver a prova de Matemática no Enem 2024? Veja as dicas do professor
Por Melina Zanotto | 08 de novembro
Confira as orientações e estratégias do professor Lucas Borguezan para se sair bem na prova de Matemática no Enem 2024.

Aulão Enem de Matemática: revisão intensiva e gratuita para a prova
Por João Vianney dos Valles Santos | 11 de outubro
Assista ao Aulão Enem de Matemática do Curso Enem Gratuito e revise os conteúdos mais importantes para a prova.


