Função de 2º Grau: como resolver com a Fórmula de Bhaskara

(UEG GO/2019)    

Em um jogo de futebol, um jogador chuta uma bola parada, que descreve uma parábola até cair novamente no gramado. Sabendo-se que a parábola é descrita pela função y = 20x – x², a altura máxima atingida pela bola é

(UNICAMP SP/2019)    

Sejam a e b números reais positivos. Considere a função quadrática f (x) = x (ax + b), definida para todo número real x. No plano cartesiano, qual figura corresponde ao gráfico de y = f (x)?

(UFT TO/2019)    

Ao realizar o estudo de sua produção diária, uma cozinheira que faz e vende pamonhas, descobriu que o lucro em reais é calculado pela função 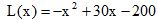onde x é o número de pamonhas feitas e vendidas. Com base nestas informações, é CORRETO afirmar que o lucro máximo diário da cozinheira é:

(Faculdade Santo Agostinho BA/2018)    

Um fabricante vende, mensalmente, x unidades de um determinado artigo. O lucro desse fabricante foi modelado, matematicamente, através da função f, dada por f (x) = –x² + 16x – 7. Quantas unidades desse artigo devem ser vendidas, mensalmente, para que o lucro do fabricante seja máximo?

(FPS PE/2018)    

A frequência máxima de batimento cardíaco de um indivíduo, FC_max, em batimentos por minuto, depende da idade, x, do indivíduo, dada em anos. Um estudo concluiu que a relação entre FC_max e x é dada por uma função quadrática:

FC_max = 163 + 1,16x – 0,018x²

Admitindo a veracidade do estudo, para qual idade temos que FC_max assume seu maior valor? Indique o valor inteiro mais próximo do valor obtido, em anos.

(UNITAU SP/2018)    

Sobre o gráfico da função definida no conjunto dos números reais por f(x) = 2x² – 4x – 6, pode-se afirmar, CORRETAMENTE, que

(Mackenzie SP/2018)    

Se f (x) = ax² + bx + c é tal que f (2) = 8, f (3) = 15 e f (4) = 26, então a + b + c é igual a

(UNIRG TO/2018)    

Em um terreno, deseja-se fazer uma cerca retangular usando-se tela em três lados do retângulo. Sabendo-se que são necessários 500 metros de tela para cercar o terreno, a função que representa a área A a ser cercada em função da medida x do lado será dada por:

(Universidade Iguaçu RJ/2018)    

Um forno autoclave é pré-aquecido e mantém sua temperatura constante. Admitindo-se que a temperatura de pré-aquecimento, em graus centígrados, é dada por F(t) = 25 + 20t, se 0  t < 5 e F(t) = t² + 10t + 50, se 5 ≤ t ≤ 15, em que o tempo t é dado em minutos, é correto afirmar que o tempo necessário para que o autoclave passe de 85ºC para 194ºC é de

(ENEM/2018)    

Um projétil é lançado por um canhão e atinge o solo a uma distância de 150 metros do ponto de partida. Ele percorre uma trajetória parabólica, e a altura máxima que atinge em relação ao solo é de 25 metros.

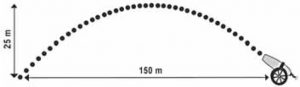
Admita um sistema de coordenadas xy em que no eixo vertical y está representada a altura e no eixo horizontal x está representada a distância, ambas em metro. Considere que o canhão está no ponto (150; 0) e que o projétil atinge o solo no ponto (0; 0) do plano xy.

A equação da parábola que representa a trajetória descrita pelo projétil é