Geometria Espacial: cálculo e área e volume. Resumo e simulado
Veja um resumo sobre Cubo e Pirâmide, e depois teste seu nível sobre geometria espacial com o simulado de Matemática do Curso Enem Gratuito. São apenas 10 questões para você aprender ou relembrar o que sabe. Se errar, tem dicas para estudar e garantir o sucesso na hora da prova. Veja só!
Todo ano caem questões envolvendo os cálculos de área em figuras de geometria plana, e os cálculos de área e de volumenas figuras da geometria espacial.
Pense nos triângulos e nos quadrados para lembrar da geometria plana. E, pense nos cubos, nos paralelepípedos e nas pirâmides quando pensar na Geometria Espacial.
Diferença entre Geometria Plana e Geometria Espacial
Na Geometria Plana você tem figuras em “2D”, com apenas duas dimensões. O desenho de um quadrado, de um círculo ou de um triângulo, o por exemplo. Eles não têm “volume”, representam apenas uma área cercada pelos lados do polígono.
Nas figuras planas você consegue fazer cálculos de Área, de Perímetro, e de ângulos. Já nas figuras de Geometria Espacial, elas têm a “terceira dimensão”, e você consegue fazer o cálculo do volume e da área da base.
Cálculo de Área em Figuras Planas
Veja com o professor Lucas Borguezan, da série Aprenda Geometria de uma vez por todas, como fazer os cálculos de Área nas Figuras Planas:
Diferenças entre Quadrado e Cubo
Você vai entender agora com o professor Lucas Borguezan, do canal do Curso Enem Gratuito, o que é a Geometria Espacial – E se liga, que não tem a ver com o espaço da astronomia, mas sim coma perspectiva de serem elementos 3D, que têm três dimensões.
Para começar, pense nas diferenças do Quadrado para o Cubo. Por exemplo, o desenho de um quadrado tem apenas duas dimensões. Ele tem apenas quatro lados. É uma figura plana.
Mas, num cubo, aí sim a coisa muda de figura, porquem entra em cena uma terceira dimensão: além ter os quadro lados que formam a base, o cubo tem ainda a dimensão que vai indicar a sua espessura, ou a sua altura. por isso ele é uma figura 3D.
Como desenhar um cubo
Acompanhe no vídeo com o professor Lucas um truque rápido para você aprender a desenhar um cubo. Isso ajuda você na hora de resolver as questões quando a figura não vem desenhada na prova.
Para desenhar um cubo, o primeiro passo é desenhar um quadrado, e depois criar um “segundo quadrado” no mesmo desenho, e depois ligar as pontas para criar um cubo.
Cálculos de Área e de Volume na Geometria Espacial
Muitas vezes as pessoas memorizam de forma errada que na Geometria Espacial se faz o cálculo de volume. E, de que na Geometria Plana se faz o cálculo de área. Mas, este raciocínio está errado, porque na Geometria Espacial também existem os cálculos de área.
O conceito de Área envolve o “espaço” que a(s) superfície(s) do objeto ocupa. E, o conceito de volume já remete à quantidade de líquido ou de outras substâncias que cabem dentro do objeto (recipiente).
O cubo consegue armazenar líquido dentro dele, indicando o volume de um cubo. Para fazer o cálculo do volume de um cubo, a fórmula básica é ver a área da base vezes a aresta dele, ou a espessura.
Se todas as dimensões forem iguais, num cubo, o volume é o resultado da multiplicação do produto dos lados pela altura.
Exercício resolvido – Como calcular a área
Veja no vídeo com o professor Lucas Borguezan como fazer o cálculo de área, por exemplo. O importante é saber o raciocínio que está por trás do cálculo que precisa ser feito.
Prismas e Pirâmides na Geometria Espacial
Confira agora com o professor de matemática Sérgio Sarkis, do canal do Curso Enem Gratuito, as dicas básicas para você gabaritar nas questões sobre Prismas, Poliedros e Pirâmides.
Conferiu com o professor Sarkis como você parte de um prisma para construir a figura de uma pirâmide? A Pirâmide vem da construção de um prisma.
Na prática, o Prisma e a Pirâmide são poliedros. Porém, a Pirâmide é dotada de uma única base, enquanto os poliedros tem “duas bases”, como explicado no vídeo acima.
Cálculo de Área e de Volume das Pirâmides
Veja agora como fazer os cálculos de Área e de Volume nas Pirâmides para você gabaritar Geometria Espacial no Enem.
Simulado de Geometria Espacial
Sumário do Quiz
0 de 10 questões completadas
Perguntas:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
Information
.
Você já fez este questionário anteriormente. Portanto, não pode fazê-lo novamente.
Quiz is loading...
You must sign in or sign up to start the quiz.
Para iniciar este questionário, você precisa terminar, antes, este questionário:
Resultados
0 de 10 perguntas respondidas corretamente
Seu tempo:
Acabou o tempo
Você conseguiu 0 de 0 pontos possíveis (0)
| Pontuação média |
|
| Sua pontuação |
|
Categorias
- Sem categoria 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- Respondido
- Revisão
-
Pergunta 1 de 10
1. Pergunta
(Fac. Israelita de C. da Saúde Albert Einstein SP/2018)
Uma peça tem a forma de uma pirâmide reta, de base quadrada, com 15 cm de altura e é feita de madeira maciça. A partir da base dessa peça, foi escavado um orifício na forma de um prisma de base quadrada. A figura mostra a visão inferior da base da peça (base da pirâmide).
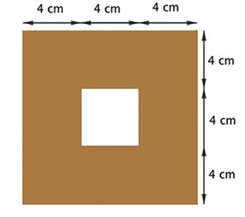
Esse orifício tem a maior profundidade possível, isto é, sem atravessar as faces laterais da pirâmide. O volume de madeira, em cm3, que essa peça contém é
CorretoParabéns! Siga para a próxima questão.
-
Pergunta 2 de 10
2. Pergunta
(PUC SP/2018)
Considere um cilindro reto de área lateral igual a 64π cm 2 e um cone reto, com volume igual a 128 π cm3, cujo raio da base é o dobro do raio da base do cilindro. Sabendo que a altura do cone é 2 cm menor do que a altura do cilindro, e que a altura do cilindro é um número inteiro, a área lateral desse cone é
CorretoParabéns! Siga para a próxima questão.
-
Pergunta 3 de 10
3. Pergunta
(UDESC SC/2018)
 Correto
CorretoParabéns! Siga para a próxima questão.
-
Pergunta 4 de 10
4. Pergunta
(UDESC SC/2018)
 Correto
CorretoParabéns! Siga para a próxima questão.
-
Pergunta 5 de 10
5. Pergunta
(ESPM SP/2018)
A figura abaixo representa a planificação da superfície lateral de um prisma triangular reto, onde as medidas x, y, z e w são números inteiros consecutivos, nessa ordem.
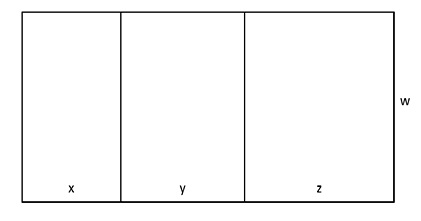
Se a soma das medidas de todas as arestas desse prisma é 42 cm, podemos afirmar que seu volume é de:
CorretoParabéns! Siga para a próxima questão.
-
Pergunta 6 de 10
6. Pergunta
(FM Petrópolis RJ/2018)
A Figura mostra um retângulo ABCD cujos lados medem 7 cm e 3 cm. Um cilindro será formado girando-se o retângulo ABCD em torno da reta definida pelo seu lado AB.
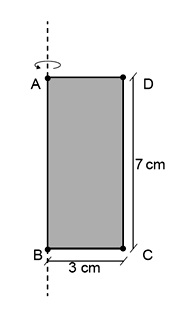
A medida do volume desse cilindro, em centímetros cúbicos, é mais próxima de
CorretoParabéns! Siga para a próxima questão.
-
Pergunta 7 de 10
7. Pergunta
(UNITAU SP/2018)
 Correto
CorretoParabéns! Siga para a próxima questão.
-
Pergunta 8 de 10
8. Pergunta
(UNCISAL/2018)
Os dados são objetos usualmente encontrados nos Laboratórios de Matemática, na forma de hexaedros, octaedros, dodecaedros e icosaedros. Os mais comuns são os hexaedros (cubos). Como desafio, um professor, não permitindo que os alunos utilizassem nenhum instrumento de medição, solicitou-lhes que resolvessem o seguinte problema: “Um cubo tem aresta x. Diminuindo-se 2 unidades de comprimento da aresta desse cubo, o seu volume diminui 98 unidades de volume. Calcule a área total do cubo de aresta x, em unidades de área (u.a)”. Para o problema solicitado pelo professor, o aluno que encontrou a resposta correta obteve como resultado
CorretoParabéns! Siga para a próxima questão.
-
Pergunta 9 de 10
9. Pergunta
(UNCISAL/2018)
A Geometria Espacial estuda as formas geométricas no espaço. Ela está presente nas abstrações da Matemática e no mundo cotidiano. Sobre essa temática, assinale a alternativa INCORRETA.
CorretoParabéns! Siga para a próxima questão.
-
Pergunta 10 de 10
10. Pergunta
(IBMEC SP Insper/2018)
A figura indica, em linha cheia, um prisma reto com faces, duas a duas, em planos perpendiculares ou em planos paralelos. Três de suas arestas medem 2x, 2x – 2 e x + 1, como indicado no desenho. O prisma está no sistema cartesiano XYZ, com uma face contida no plano XY e com arestas paralelas ao eixo x ou ao eixo y. Sabe-se, ainda, que P, Q, R, S, T, U e V são vértices do prisma, que O é a origem do sistema XYZ e que todas as medidas de comprimento da figura estão em centímetros.
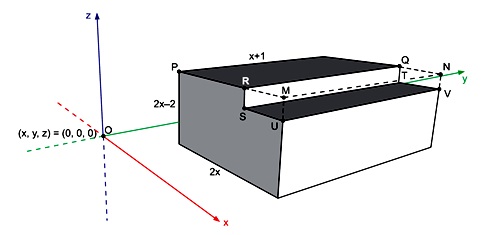
Se os volumes do prisma, indicado na figura, e do paralelepípedo reto-retângulo MRSUNQTV, tracejado na figura, são, respectivamente, iguais a 1 264 cm3 e 80 cm3, então a medida de x, em centímetros, é um número
CorretoParabéns! Siga para a próxima questão.
Sobre o(a) autor(a):
Taynara Macedo -
Gostou? Compartilhe!
Continue lendo:
Aqui vão 2 publicações relacionadas que talvez você goste:

Como resolver a prova de Matemática no Enem 2024? Veja as dicas do professor
Por Melina Zanotto | 08 de novembro
Confira as orientações e estratégias do professor Lucas Borguezan para se sair bem na prova de Matemática no Enem 2024.

Aulão Enem de Matemática: revisão intensiva e gratuita para a prova
Por João Vianney dos Valles Santos | 11 de outubro
Assista ao Aulão Enem de Matemática do Curso Enem Gratuito e revise os conteúdos mais importantes para a prova.


