Gráfico de função exponencial: propriedades e características
O gráfico de função exponencial demonstra uma alteração repentina num conjunto de informações. Entenda como ele funciona neste resumo de Matemática!
A característica principal de um gráfico de função exponencial é possuir um comportamento que demonstra que um determinado número de dados vinha com um crescimento praticamente contínuo e, de repente, transformou-se em um crescimento exponencial. É disso que você precisa lembrar na hora de estudar o gráfico da função exponencial! Geralmente o comportamento do gráfico demonstra uma alteração repentina no crescimento ou decrescimento de um determinado conjunto de informações.
Nesta aula você vai aprender como descobrir algumas informações importantes apenas observando o esboço do gráfico de uma função exponencial. Vamos lá?
Função Exponencial
Para falar sobre o gráfico da função exponencial é preciso primeiro um resumo sobre o que é a função exponencial. Uma função exponencial é qualquer função em que a variável está no expoente, e cuja base sempre é maior que zero e diferente de 1. A função se apresenta da forma:
![]()
Onde é a base com expoente x.
A base requer algumas restrições. Ela não pode ser negativa e também não pode ser igual a 1 e nem igual a zero, pois para alguns expoentes a função não estaria definida. Observe o que isso significa graficamente falando.
Gráfico da função exponencial
As restrições dadas acima podem ser vistas facilmente ao se plotar o gráfico dessas funções. Para a melhor observação do comportamento das funções utilizaremos o ferramental matemático disponível na internet. Você também pode testar este aplicativo! É bastante interessante.
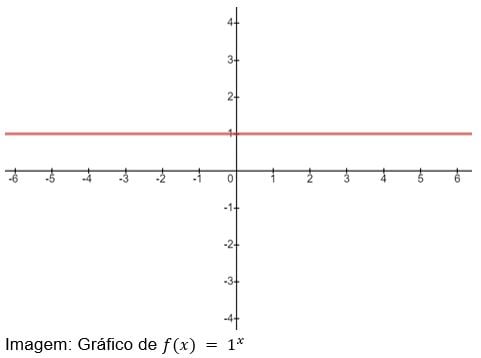
1ª restrição: a ser diferente de 1.
Esta restrição se dá pelo fato de que, ao se tratar de potenciação, o número 1 elevado em qualquer expoente será 1, já que 1 multiplicado por ele mesmo é igual a 1. Logo, o gráfico de equivale à reta .
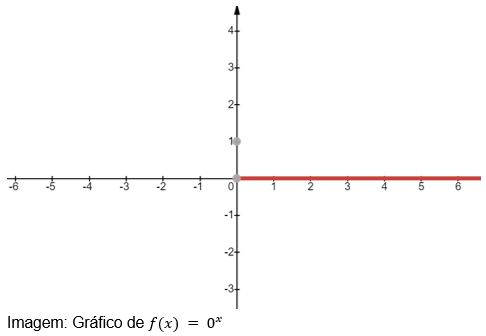
2ª restrição: a ser diferente de 0.
Da mesma forma que a primeira restrição, não existem valores negativos que satisfaçam ![]() . Portanto, a função não é definida. Já para valores positivos, a função é definida, mas equivale a uma constante.
. Portanto, a função não é definida. Já para valores positivos, a função é definida, mas equivale a uma constante.
3ª restrição: a ser maior do que zero.
A função exponencial não admite valores negativos para a base da potência pois os resultados para f(x) não são constantes. Dessa forma, não é possível construir um gráfico com valores reais.
Faça você mesmo o teste e tente plotar uma função ![]() para ver o que acontece!
para ver o que acontece!
Propriedades do gráfico da função exponencial
Tendo em vista as restrições aplicáveis ao gráfico da função exponencial, vamos agora ver algumas das suas propriedades.
1ª propriedade
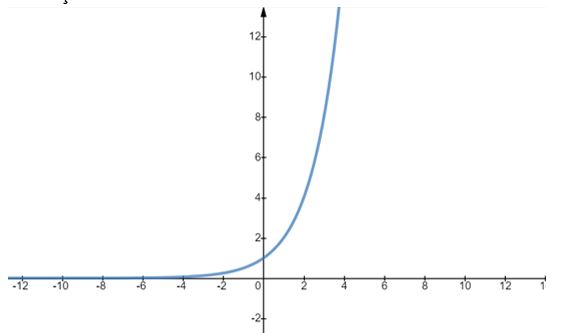
Se a base a da função exponencial for maior que 1 (a>1) então, o gráfico da função será crescente.
2ª propriedade
Se a base da função exponencial a se encontrar no intervalo entre 0 e 1, então o gráfico da função se comporta de maneira decrescente. Isso se dá pelo fato de que números menores do que 1 elevados a alguma potência equivalem a números ainda menores.
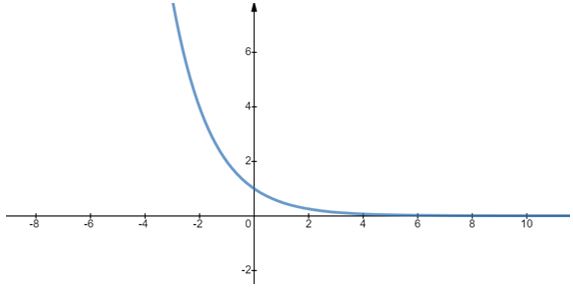
Importante: perceba que nos exemplos acima, o gráfico sempre “corta” o eixo Y no ponto (0,1). Isso ocorre pelo fato de que qualquer número elevado a zero é igual a 1, ou seja,
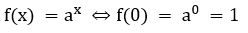 3ª propriedade
3ª propriedade
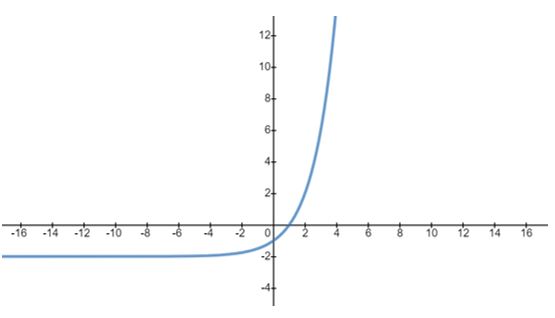
O gráfico da função exponencial sempre se localiza acima do eixo x. Pela definição, a base da função exponencial sempre será maior que zero em toda a função exponencial. Isso significa que os valores de f(x) correspondentes a Y nunca serão negativos. Sendo assim, assumem valores muito próximos a zero, mas nunca iguais ou menores que zero.
É importante considerar o fato de que essa propriedade só é válida para funções exponenciais que se apresentam de forma simples, veja o exemplo:
Exemplo: Gráfico da função ![]()
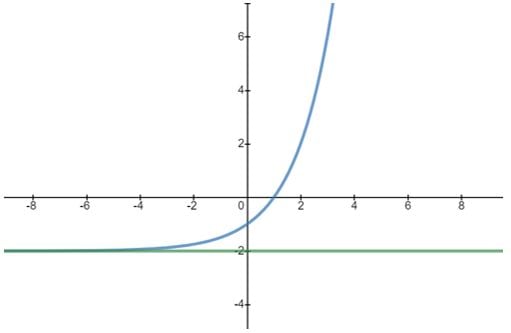
Em casos como este, perceba que o gráfico inteiro de ![]() deslocou-se duas unidades abaixo em relação ao eixo X, assumindo, assim, valores menores que zero, mas não menores do que dois.
deslocou-se duas unidades abaixo em relação ao eixo X, assumindo, assim, valores menores que zero, mas não menores do que dois.
Nesse caso, o gráfico da função admite uma assíntota horizontal onde os valores de f(x) = y serão muito próximos a essa assíntota, mas nunca menores ou iguais a ela.
Como exercício, sugiro utilizar qualquer ferramental matemático para plotagem de gráficos e fazer experimentações, somando e subtraindo termos tanto no expoente quanto na base da função exponencial e prestando atenção em como se comportam os gráficos resultantes.
Videoaula
Relembre como resolver funções exponenciais com a videoaula do nosso canal:
Exercícios
Questão 01)
A intersecção dos gráficos das funções f(x) = 3x e 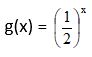 é
é
a) um ponto sobre o eixo das abscissas
b) um ponto de ordenada negativa
c) um ponto no 1º quadrante
d) a origem do sistema
e) o ponto (0,1)
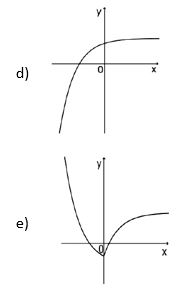
Questão 02)
Ao abrir um negócio, um microempresário descreveu suas vendas, em milhares de reais (unidade monetária brasileira), durante os dois primeiros anos. No primeiro ano, suas vendas cresceram de modo linear. Posteriormente, ele decidiu investir em propaganda, o que fez suas vendas crescerem de modo exponencial.
Qual é o gráfico que melhor descreve as vendas em função do tempo?
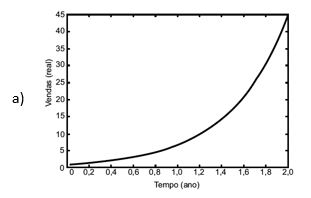
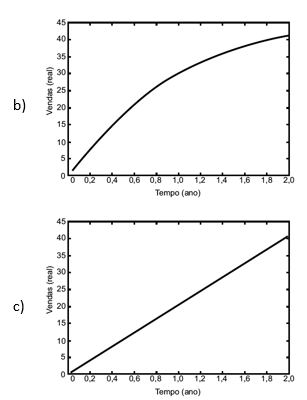
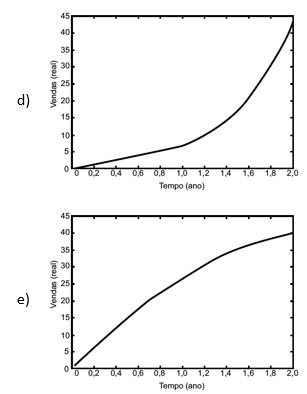
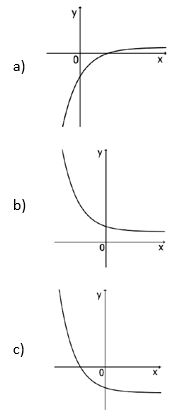
Questão 03)
Considere a função f definida por ![]() e representada em um sistema de coordenadas cartesianas.
e representada em um sistema de coordenadas cartesianas.
Entre os gráficos abaixo, o que pode representar a função f é
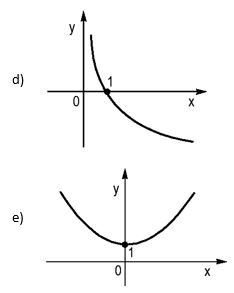
Questão 04)
Uma possível representação gráfica da função definida por f(x) = 10–x é:
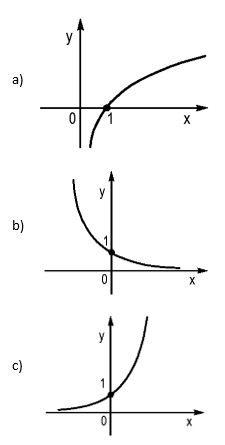
01) Gab: E
02) Gab: D
03) Gab: A
04) Gab: B





