Veja o que é uma função exponencial e quais são as suas características. Estude Matemática para o Exame Nacional do Ensino Médio com o Curso Enem Gratuito.
A função exponencial pode aparecer nas questões de várias disciplinas na prova do Enem. Por exemplo, ela surge nos estudos de tratamento da informação (como crescimento e decréscimo populacional), nos decaimentos radioativos, crescimento de populações bacterianas e em seus controles entre tantos outros estudos fascinantes.
Na economia, os gráficos de funções exponenciais aparecem a todo instante. A função exponencial nos dá informações e a possibilidade de interpretar eventos importantes.
Com esses dados, por exemplo, podemos prever e prevenir danos colaterais como uma superpopulação de bactérias em um ser humano doente. No plano cartesiano, o gráfico da função exponencial nos dá um gráfico com uma curva exponencial.
Função exponencial
Com isso, posso te afirmar que é muito importante entender como interpretar esse tipo de função e seus respectivos gráficos. Vamos lá começar com um resumo básico, um “esquenta”, para você conseguir identificar e calcular as funções nas provas do Enem e dos vestibulares.
Como resolver funções – Confira agora com o professor de matemática Lucas Borguezan, do canal do Curso Enem Gratuito, as dicas que vão te proteger em todas as provas:
Como é uma função exponencial
Dizemos que uma função exponencial se escreve da seguinte forma:
Onde os símbolos representam:
- f(x) : função
- a: número Real, positivo (a>0) e diferente de 1.
- x: variável independente, sendo um número Real.
Características da função exponencial
- a > 0 se a fosse igual a zero teríamos uma função
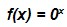e para x = 0 , a função 
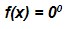tem um valor indeterminado. E não chegamos a lugar algum.- a ≠0 se a for igual a zero , não temos mais uma função exponencial. Ela seria uma função constante. Veja:
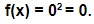
- Para qualquer valor de x a função terá sempre o valor zero, menos quando x = 0, que é indeterminado como vimos.
O Domínio e a Imagem dessa função são definidas como:
( números Reais positivos e diferentes de zero).
Exemplos
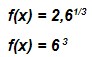
Função natural
Uma função exponencial muito utilizada é aquele que a assume o valor neperiano, número representado pela letra e. Seu valor é dado por uma dízima não periódica que é: e = 2,718281828459…
Esse número foi descoberto por John Napier ao inventar os logaritmos em 1614. Mas, quem deu o símbolo a esse número foi Euler em 1739.
Essa função exponencial é denominada função natural e toma a forma:
sendo 
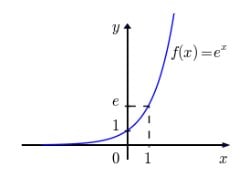
Comportamento da função exponencial
A função exponencial tem alguma características em relação a seu comportamento e em relação ao seu crescimento/decrescimento:
- a > 0: acima do eixo x.
- a > 1: a função tende a zero quando x se aproxima de valores negativos.
- a > 0 e a ≠1: os pontos
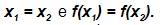
- 0 < a < 1: a função tende a zero quando x assume valores positivos.
- x = 0: então
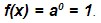
Isso quer dizer que a curva corta o eixo y no ponto P(0,1)
Classificação quanto ao crescimento ou decrescimento
Toda a função exponencial pode ser classificada em relação ao seu crescimento ou decrescimento como:
- Crescente: quando a > 1.
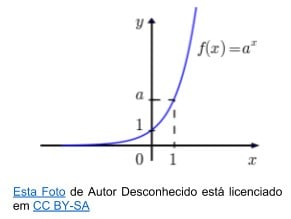
Neste gráfico, a curva se aproxima do zero quando x assume valores negativos.
- Decrescente: quando 0 < a < 1.
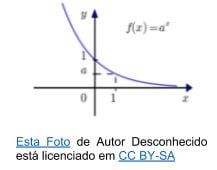
Perceba que a curva do gráfico tende a zero para valores de x positivos.
Uma função importante de ser estudada é a logarítmica, essa função é a inversa da função exponencial. E no Enem e nos vestibulares muitas questões envolvem os dois assuntos.
Exercício resolvido
(PUCC-SP) Numa certa cidade, o número de habitantes, num raio de r m a partir do seu centro é dado por 
em que k é constante e r > 0. Se há 98 304 habitantes num raio de 5 km do centro, quantos habitantes há num raio de 3 km do centro?
Solução:
Sabemos do enunciado do problema que
P(r) = 98 304 habitantes.
r = 5 km
Esses valores deverão ser substituídos na função dada, onde o asterisco simboliza uma multiplicação:
Vamos calcular a constante k:
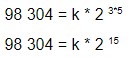
Na etapa acima, devemos elevar a base 2 à 15ª potência, que é igual a 32 768.
98 304 = k * 32 768
k = 3 (
O objetivo da resolução é o cálculo do número de habitantes num raio de 3 km, então usamos a mesma função só que substituímos r por 3: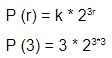
Multiplicamos os expoentes:
Elevamos a base 2 à 9ª potência, que dá 512:
P (3) = 3 * 512
Multiplicamos e está pronto!
P(3) = 1536
Encontramos o número de habitantes num raio de 3 km é igual a 1536.
Videoaula sobre função exponencial
Exercícios
1) (UERJ-1998) Uma empresa acompanha a produção diária de um funcionário recém-admitido, utilizando uma função f(d), cujo valor corresponde ao número mínimo de peças que a empresa espera que ele produza em cada dia (d), a partir da data de sua admissão. Considere o gráfico auxiliar, que representa a função 
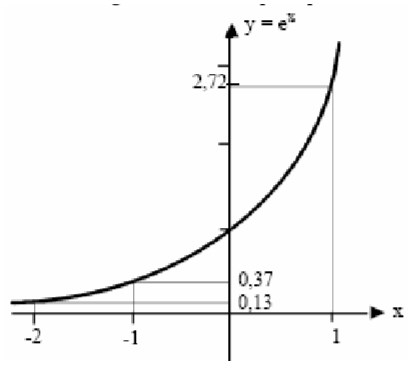
Utilizando 
e o gráfico acima, a empresa pode prever que o funcionário alcançará a produção de 87 peças num mesmo dia, quando d for igual a :
a) 5
b) 10
c) 15
d) 20
2) (Vunesp-2003) Num período prolongado de seca, a variação da quantidade de água de certo reservatório é dada pela função q(t) = q0.2(-0,1)t sendo 
a quantidade inicial de água no reservatório e q(t) a quantidade de água no reservatório após t meses. Em quantos meses a quantidade de água do reservatório se reduzirá à metade do que era no início?
a) 5.
b) 7.
c) 8.
d) 9.
e) 10.
3) (PUC-PR-2003) Determinando as soluções da equação 
verificamos que elas estão somente no intervalo:
I. (0, 1) se a > 1.
II. (1, ∞) se 0 < a < 1. III. (-∞, 0) se a > 1.
IV. (-1, 1) se 0 < a < 1.
Com respeito às afirmações acima, podemos afirmar que:
a) exatamente duas são verdadeiras.
b) todas as afirmações são falsas.
c) somente uma é verdadeira.
d) somente uma é falsa.
e) todas as afirmações são verdadeiras.
Gabarito:
1) b;
2) e;
3) c
Bibliografia:
Telecurso 2000 – aula 10. Disponível em https://youtu.be/WXMm5sJzMpk.
Khan Academy. Análise de gráficos de uma função exponencial . Disponível em: https://goo.gl/SYGsUg.
Oliveira, Rafael H. Um Estudo Sobre A Função Exponencial. UNESP. Rio Claro.2015.
