Inequações logarítmicas

O conceito de desigualdade é bastante abrangente, já que, na matemática, quando dois termos não são iguais eles não são classificados como diferentes. Ainda é possível identificar as relações de maior, menor, maior igual e menor igual. No estudo dos logaritmos também utilizamos as desigualdades para relacionar termos. Na aula de hoje você vai ver como isso acontece, além de algumas propriedades das inequações logarítmicas. Acompanhe a aula, preste atenção nos exemplos e, ao final, tente solucionar os exercícios.

Equação Logarítmica

Antes de começar a aula sobre inequações logarítmicas, é importante você brevemente lembrar o que é uma equação logarítmica. Uma equação logarítmica é a equação que apresenta incógnita no logaritmo e pode ser redutível a uma igualdade entre dois logaritmos de mesma base.

Além disso, para um resultado ser considerado solução da equação, ele precisa necessariamente obedecer às condições de existência do logaritmo.

Importante: Condições de existência do logaritmo:

1. A base do logaritmo deve ser positiva e diferente de 1;
2. O logaritmando deve ser positivo.

Para entendermos melhor, vamos ver um exemplo:

Exemplo: Resolva a equação

Solução: Como as bases dos logaritmos (base 2) na igualdade são iguais, a solução é dada por:

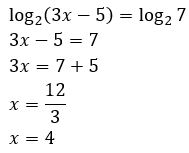
Fazendo a “prova real” verificamos que X = 4 é solução da equação proposta, pois 7 > 0 é satisfeita para todo X real.

Inequações Logarítmicas

Para solucionar inequações logarítmicas, utilizamos a mesma linha de raciocínio da solução de equações logarítmicas, sempre prestando atenção nas condições de existência do logaritmo. As inequações logarítmicas são classificadas em três tipos básicos que possuem regras específicas na hora da resolução. Veja a seguir.

Primeiro tipo de inequação logarítmica

Essa é uma inequação que pode ser reduzida a uma desigualdade entre dos logaritmos de mesma base a (com ‘a’ positivo e diferente de 1). É preciso levar em consideração que a base do logaritmo influencia diretamente na função logaritmo, esta é crescente caso a > 1, e decrescente se 0 < a < 1. Tendo isso em vista, consideraremos dois casos:

Caso 1: quando a base é maior que 1, a relação de desigualdade entre os logaritmandos possui o mesmo sentido que a dos logaritmos. Assim:

O argumento  está destacado em vermelho para que você não esqueça: a condição de existência de um logaritmo em  é que os logaritmandos sejam positivos.

Exemplo: Resolver a inequação

Solução: A base 3 é maior que 1, logo, a desigualdade entre os logaritmandos tem o mesmo sentido que a dos logaritmos

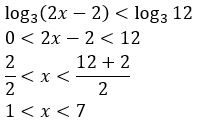Isso significa que, para todos os valores de x entre 1 e 7, a inequação  é satisfeita, logo o conjunto solução é:

Caso 2: Quando a base é menor que 1, a relação de desigualdade entre os logaritmandos é de sentido contrário ao dos logaritmos. Além disso, a condição de existência de um logaritmo em  é que os logaritmandos sejam positivos. Assim:

Sempre verifique as condições de existência e faça o estudo de sinal quando for necessário. Pode também separar os logaritmandos para não causar nenhuma confusão.

Segundo tipo de inequação logarítmica

Essa é uma inequação logarítmica que pode ser reduzida a uma desigualdade entre um logaritmo e um número real. Para isto, basta lembrarmos da propriedade dos logaritmos que nos diz que o número k pode ser expresso da forma:

Em palavras, é como se um número k que multiplica um logaritmo de base e logaritmando iguais pudesse “saltar” para o expoente do logaritmando.

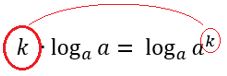
Então, temos as inequações:

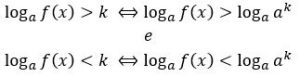Exemplo: Resolva a inequação a seguir:

Solução: Usando a propriedade, temos que:

Resolvendo:

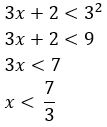Além disso, é preciso levar em consideração a condição de existência logaritmando positivo, então:

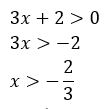Então, a solução da inequação são todos os termos maiores do que – 2/3 e menores do que 7/3, logo:

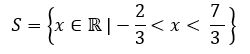
Terceiro tipo de inequação logarítmica: incógnita auxiliar 

Esse é um tipo de inequação que gera bastante dúvida entre os (as) estudantes, pois muitas vezes buscam os piores caminhos para solucionar uma questão onde basta substituir o logaritmo por uma incógnita auxiliar. Veja o exemplo.

Exemplo: Resolva a inequação:

Solução: Perceba que ocorre uma repetição, o termo  pode ser substituído por uma incógnita, por conveniência, escolhemos y. Assim:Por soma e produto, as raízes dessa equação são 2 e 3, então y > 2 ou y > 3, mas , então:

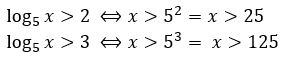
Como os termos que são maiores que 25, mas menores que 125, não satisfazem a inequação, então o conjunto solução desta inequação é:

Gostou dessa aula? Bastante coisa para compreender não é mesmo?

Agora veja nossa aula sobre as inequações logarítmicas e continue estudando:

Relembre o conteúdo de logaritmos com o vídeo do nosso canal:

Exercícios:

Questão 01)  O conjunto solução da inequação  é:

 

 

 

 

 

 

 

 

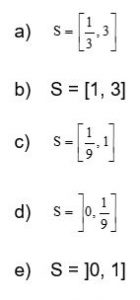
Questão 02) Considere a função . A quantidade de números inteiros que pertencem ao conjunto solução da inequação  é igual a:

a) 8

b) 12

c) 21

d) 19

e) 11

 

Questão 03)    

O conjunto solução da inequação  no conjunto dos números reais é

 

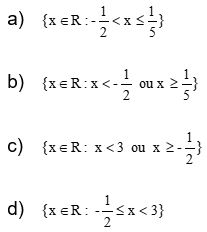
01) Gab: C

02) Gab: E

03) Gab: A

Compartilhe: