Como calcular o mínimo múltiplo comum (MMC)
Aprenda a resolver questões do Enem usando métodos rápidos como o MMC, o Mínimo Múltiplo Comum! Veja agora com aula gratuita, exemplos e exercícios resolvidos.
O mínimo múltiplo comum tem inúmeras aplicações. Mas, geralmente utilizamos o MMC para adicionar ou subtrair frações com denominadores diferentes, não é mesmo? Só que não é só para isso que o MMC serve.
Podemos resolver inúmeros problemas usando somente o processo de fatoração ou de múltiplos de um número. E é isso que vamos mostrar para você!
Introdução ao cálculo de MMC
Para ajudar você a aprender de vez sobre como calcular o Mínimo Múltiplo Comum, e tirar as dúvidas restantes, veja o resumo com o professor Lucas, do canal do Curso Enem Gratuito:
Mínimo Múltiplo Comum
Vem com a gente revisar mais este conteúdo de Matemática Básica para mandar bem no Enem!
Atualmente parecemos viver em função do tempo. O relógio, às vezes, aparenta trabalhar rápido demais. Mas, não. Ele trabalha de hora em hora, minuto a minuto, segundo a segundo. E horas, minutos e segundos são múltiplos de 60.
E mais, os minutos do relógio são representados em intervalos de 5 em 5 minutos. Como podemos ver, ao vivermos sob o comando do relógio, vivemos em função dos múltiplos. Então, porque não estudar sobre eles?
Exemplo de MMC
Para entendermos como são os múltiplos, como a divisão de uma hora em um relógio, vamos começar pelo conceito de Mínimo Múltiplo Comum. Bello ( 2007, p.9) diz que:
“Para dois ou mais números existirão infinitos múltiplos comuns a esses dois números . O M.M.C será o menor desses infinitos múltiplos comuns.”
Para entendermos melhor o que isso quer dizer, vamos pensar em um exemplo. Determine o MMC entre 15 e 20:
O MMC entre dois números a e b é representado por MMC(a,b).
M(15) = {15, 30, 45, 60, 75, 90, 105, 120, …}
M(20) = { 20, 40, 60, 80, 100, 120, …}
Compare os dois conjuntos e procure o primeiro e menor múltiplo comum aos dois. Vamos marcar de vermelho nos próprios conjuntos
M(15) = {15, 30, 45, 60, 75, 90, 105, 120, …}
M(20) = { 20, 40, 60, 80, 100, 120, …}
Esse é o MMC (15, 20) = 60.
Como você pode ver, a comparação entre os conjuntos de múltiplos de dois números é um dos métodos de resolução com o MMC. Vamos estudar outros?
Você sabe o que é um múltiplo? O que é um divisor? Acesse a aula sobre Múltiplos e Divisores de um número.
Propriedades do Mínimo Múltiplo Comum
a) Múltiplos entre si:
Se dois números a e b forem múltiplos entre si ( são da mesma tabuada), o MMC entre esses números será igual ao maior deles.
MMC(a,b) = b
Exemplo: Calcule o MMC entre 4 e 12:
MMC(4,12) = 12
b) Números primos entre si:
Se dois números a e b forem primos entre si, o MMC entre eles será igual ao produto entre eles.
MMC(a,b) = a x b
Exemplo: Qual é o MMC entre 7 e 23?
MMC(7,23) = 7 . 23 = 161
c) Consecutivos:
Se dois números a e b forem consecutivos, o MMC entre eles será igual ao produto entre eles.
MMC(a,b) = a x b
Exemplo:
MMC (11,12) = 11 . 12 = 132
Como calcular o MMC
a) Fatoração em separado:
Para o cálculo do MMC entre a e b, fatoramos os números em separado. O MMC será o produto de todos os fatores primos, tomando sempre os maiores expoentes dos fatores comuns.
Exemplo: Qual é o MMC entre 12 e 34?

b) Fatoração simultânea:
Fatoramos todos os números ao mesmo tempo. O resultado da fatoração será o MMC entre eles.
Exemplo: Qual o MMC entre 12 e 34?
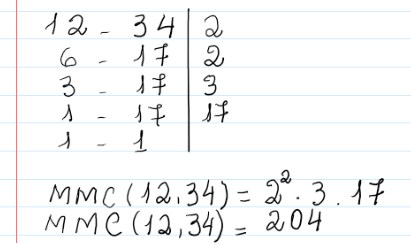
Neste caso, dividimos 12 e 34 por 2. Em seguida, escrevemos os resultados abaixo deles. Como 6 é par dividimos por 2 e 17 ficou na espera. Foi reescrito na terceira linha.
Na terceira linha ficamos com 3 e 17 e, então, dividimos pelo número primo menor que é 3. O 17 ficou na espera novamente.
Na quarta linha dividimos 17 e o resultado na quinta linha foi 1 e 1, o que indica que acabou a fatoração.
Exercícios Resolvidos de MMC
1) (Enem 2014) A maior piscina do mundo, registrada no livro Guiness, está localizada no Chile, em San Alfonso del Mar, cobrindo um terreno de 8 hectares de área. Sabe-se que 1 hectare corresponde a 1 hectômetro quadrado. Qual é o valor, em metros quadrados, da área coberta pelo terreno da piscina?
A) 80
B) 800
C) 8.000
D) 80.000
Resolução:
A resolução desse problema está no conceito de múltiplos de um número.
Sabemos que 1hm² = 10.000 m²
e o enunciado informa que 1 há = 1 hm²
Com isso podemos dizer que: 8ha = 8hm²
Substituindo a primeira informação na relação acima, chegamos a:
8 . 10000 = 80.000 m²
A alternativa correta é a D.
2) (UFMG – adaptado) Num determinado país, o presidente deve permanecer 4 anos em seu cargo; os senadores, 6 anos e os deputados, 3 anos. Nesse país, houve eleição para os três cargos em 2012. A próxima eleição simultânea para esses três cargos ocorrerá, novamente, em que ano?
A) 2016
B) 2015
C) 2024
D) 2022
E) 2019
Resolução:
Para determinar daqui a quantos anos teremos nova eleição simultânea entre os três poderes, precisamos fatorar 3 , 4 e 6 simultaneamente.

MMC (3 , 4 , 6) = 12.
Para determinarmos a data da próxima eleição simultânea basta somar o valor do MMC com o ano da última eleição:
2012 + 12 = 2024.
Alternativa C.
Exercícios sobre Mínimo Múltiplo Comum
1) (Unicamp-SP)
Numa linha de produção, certo tipo de manutenção é feito na máquina A a cada 3 dias, na máquina B a cada 4 dias e na máquina C a cada 6 dias. Se no dia 2 de dezembro foi feita a manutenção nas três máquinas, a próxima vez em que a manutenção das três ocorreu no mesmo dia foi:
A) 5 de dezembro.
B) 6 de dezembro.
C) 8 de dezembro.
D) 14 de dezembro.
E) 26 de dezembro
2) (UFPE)
Um ônibus chega a um terminal rodoviários a cada 4 dias. Um segundo ônibus chega ao terminal a cada 6 dias e um terceiro, a cada 7 dias. Numa ocasião, os três ônibus chegaram ao terminal no mesmo dia. A próxima vez em que chegarão juntos novamente, ao terminal ocorrerá depois de:
A) 60 dias
B) 35 dias
C) 124 dias
D) 84 dias
E) 168 dias
3) (Enem 2013)
Uma dona de casa faz um comparativo de custos para decidir se irá adquirir uma máquina lavadora de louças para substituir a lavagem manual. Decide calcular o custo com a lavagem de louças por um período de 30 dias, com duas lavagens por dia.
Ela constatou que não precisa considerar os custos do detergente e do sabão, pois, na máquina lavadora e na lavagem manual, são equivalentes. Verificou que gasta em média 90 litros de água em cada lavagem manual. Cada lavagem na máquina gasta 16 litros de água e 0,9 kWh de energia.
Sabe-se que a companhia de distribuição de água cobra R$ 6,25 por metro cúbico (pelo consumo de água e dispersão e tratamento de esgoto) e a companhia elétrica cobra R$ 0,45 por kWh consumido.
De acordo com essas informações, num período de 30 dias, a lavagem manual ficará mais cara que a da máquina lavadora em quantos reais?
A) 1,72
B) 3,45
C) 4,72
D) 9,45
E) 27,75
Gabarito:
1 – D
2 – D
3 – B
Referências sobre MMC – Mínimo Múltiplo Comum:
BELLO, Pedro. Matemática Básica para Concursos v.1.Rio de Janeiro: ED. Ferreira, 2007.
Imagens: Portal e- UNICAMP e Wikimedia Commons.
Quer resolver mais exercícios?
Veja aqui mais uma aula completa de Múltiplos e Divisores Comuns





