Como resolver operações com conjuntos numéricos
Muita gente se confunde na hora de efetuar operações com conjuntos numéricos. Mas, nesta aula, você vai tirar todas suas dúvidas para arrasar em Matemática no Enem e vestibulares!
Quem nunca se confundiu na hora de fazer operações com conjuntos numéricos, não é mesmo? Muitas vezes, por se tratarem de conjuntos de muitos elementos, alguns alunos podem se atrapalhar na hora de realizar as operações, como a União e a Intersecção.
Realmente é preciso bastante atenção para não deixar nenhum elemento do conjunto numérico de lado na hora da operação.
Mas, com um pouco de paciência, muito estudo e treinamento, pode aparecer qualquer conjunto numérico que você vai saber direitinho o que fazer com ele. Então, vamos juntos conhecer algumas dessas operações?
Introdução às operações com os Conjuntos Numéricos – Veja com o professor Lucas Borguezan, do canal do Curso Enem Gratuito, as dicas básicas para você gabaritar nas Operações.
Antes de continuarmos pensando nas operações com conjuntos, dá uma olhada na imagem aí embaixo para lembrar quais são os tipos de conjuntos numéricos.
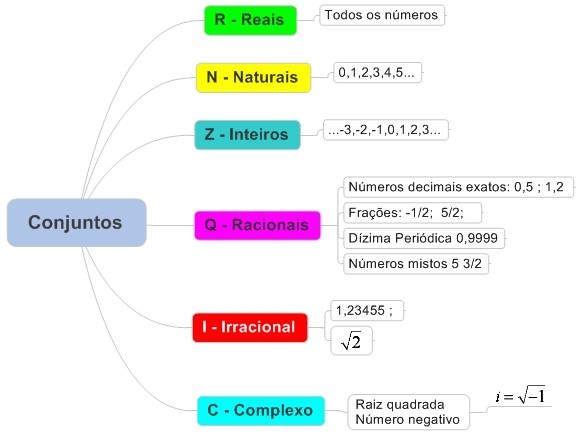
Importante: Quando formos efetuar uma operação com um conjunto numérico, na verdade estamos realizando uma operação com os elementos desse conjunto.
Vamos ver agora cada uma das operações com conjuntos numéricos, separadamente.
União de conjuntos
Para calcular a união de dois ou mais conjuntos basta fazer o que o próprio verbo nos diz: unir os elementos de um conjunto com os elementos do outro. Ou seja, o conjunto união é formado pelos elementos de um conjunto e os elementos de outro conjunto.
O conjunto União é representado pelo símbolo U. Veja os exemplos:
- Exemplo 1: Dados os conjuntos A = {3,4,5,6} e B = {8,9,10,11} , represente a união entre os dois conjuntos.
Resposta: o conjunto da união de A e B vai ser representado por A U B, e seus elementos serão todos os elementos de A e todos os elementos de B:

- Exemplo 2: Gabriela e Marina estão estudando para o vestibular, Gabriela está estudando o conjunto de matérias H = {História, Filosofia, Geografia, Química}, enquanto Marina está estudando o conjunto de matérias I = {Inglês, Química, Matemática, Física}. Se forem estudar juntas, qual será a união de todas as suas matérias?
Resposta: Iremos representar por H U I a união de todos os elementos (matérias que estão sendo estudadas). Logo:
H U I = {História, Filosofia, Geografia, Química, Inglês, Matemática, Física}
Atenção! Você percebeu que Química, apesar de aparecer nos dois conjuntos, apareceu uma única vez no conjunto união? Lembre-se desta propriedade, no caso de um elemento se repetir nos dois conjuntos, no conjunto união só aparecerá uma vez.
Intersecção de conjuntos
Embora a união de conjuntos se assemelhe bastante com a soma, a intersecção é bem diferente. Para realizar a intersecção entre dois conjuntos, devemos considerar os elementos que aparecem em ambos conjuntos e descartar os elementos que não são comuns aos dois.
A intersecção é representada pelo ∩, símbolo inverso da união.
- Exemplo 1: Dados os conjuntos I = {1,3,5,7,9,11,13,15} e P = {2,3,5,7,11,13} , apresente a intersecção ∩ entre os dois conjuntos.
Resposta: podemos verificar que os elementos que se repetem nos dois conjuntos são os numerais 3, 5, 7, 11, 13. Já os numerais 1, 9, 15 e 2 só aparecem em um conjunto. Logo, o conjunto Intersecção será dado por:
I ∩ P = {3,5,7,11,13}
- Exemplo 2: Dados os conjuntos A = {-4, – 3, -2, -1, 0} e B = {0, 1, 2, 3, 4}, apresente a intersecção ∩ entre os dois conjuntos.
Resposta: Perceba que o único elemento que se repete em ambos conjuntos A e B é o elemento 0, logo a intersecção entre A e B será dada por:
A ∩ B = {0}
Diferença de conjuntos
Para calcular a diferença entre dois conjuntos é preciso prestar atenção na ordem em que os conjuntos são apresentados. Ou seja, devemos efetuar a diferença de um conjunto A por um conjunto B é representar no conjunto final A – B, todos os elementos de A que não pertencem ao conjunto B. Na verdade, o que acontece é que eliminamos os elementos correspondentes aos dois conjuntos. Veja o exemplo numérico para sintetizar:
- Exemplo 1: Dados os conjuntos X = {5,10,15,20,25,30,35,40} e Y = {10,20,30,40} , a diferença entre os conjuntos, dada por X-Y é dada por:
Resposta: Temos X = {5,10,15,20,25,30,35,40} – Y = {10,20,30,40} e os elementos que se repetem são 10, 20, 30, 40, logo:
X – Y = {5,15,25,35}
- Exemplo 2: Dados os conjuntos A = {-3, -2, -1} e B = {-7, -6, -5, -3}, B-A é igual a:
Resposta: esse exemplo nos faz perceber como a ordem dos conjuntos é importante, além do mais, os elementos que aparecem em A e não aparecem em B não são considerados aqui. Então, o resultado de B-A é:
B – A = {-7, -6, -5}
Vamos resolver alguns exercícios para fixar ainda mais esse conteúdo?
(PUC-RJ) Sejam x e y números tais que os conjuntos {0, 7, 1} e {x, y, 1} são iguais. Então podemos afirmar que:
a) a = 0 e y = 5
b) x + y = 7
c) x = 0 e y = 1
d) x + 2y = 7
e) x = y
R: alternativa B
Considerando os conjuntos A = { 1, 2, 3} , B = { 2, 3 ,5} e C = { 1, 3, 7, 8} execute as operações abaixo:
a) A U B ∩ C
b) (AUB)∩C
c) (AUC) – B
d) (B∩C) – A
R: a) {1,2,3,5,7,8}
b) {1,3}
c) {1,7,8}
d) VAZIO





