Como resolver operações com polinômios
A base do cálculo algébrico é fundamental na resolução da maioria dos problemas envolvendo Matemática apresentados em vestibulares e no Enem. Nessa aula, você vai aprender a resolver operações com polinômios.
A linguagem matemática e a álgebra fazem parte da maioria dos temas das ciências exatas que estudamos para a prova do Enem. Seja na Matemática, na Física ou na Química, quase sempre nos deparamos com problemas envolvendo operações com polinômios.
Expressões algébricas
As expressões algébricas são aquelas expressões em que números e variáveis coexistem. Essas expressões podem ser nomeadas pelo número de termos algébricos:
- Monômio: um termo algébrico, como 5x².
- Binômio: possui dois termos algébricos, como ax² + 3.
- Trinômio: três termos algébricos, como 4a² +3b³ – 2.
- Polinômios: mais de três termos algébricos, como 7c – 2b + 3t² + 5ª.
Aprenda a resolver Polinômios
Confira agora o ABC dos polinômios com o professor Lucas Borguezan, do canal do Curso Enem Gratuito:
O que são polinômios
Os polinômios são as expressões mais utilizadas. Seu grau é dado pelo valor do maior expoente de uma de suas variáveis(letras). Veja alguns exemplos:
a) 2d2 + 7a²c³ + 2tk – x3, o expoente maior aqui é o 3, então o polinômio é de 3º grau.
b) 5at3 + 27a²b³ – 12 t + 3k5 , nesse caso grau 5.
Operações com polinômios
Agora que você já relembrou o que é um polinômio, vamos começar a estudar as operações com polinômios.
Adição e subtração com polinômios
Para resolver uma adição ou subtração de polinômios, você precisa fazer os seguintes procedimentos:
1º) Elimine os sinais de associação, se tiver.
2º) Reúna os termos semelhantes (aqueles que têm a mesma letra e o mesmo expoente) e reduza-os. E pronto!
Observe o exemplo abaixo:
(-10x³ + 2x² – x) + (-12x³ – 9x) – (3x² + x) =
Em primeiro lugar, tiramos os parênteses. Cuidado com o sinal negativo, ele indica que ao tirarmos os parênteses temos que trocar os sinais de todas os termos que estão dentro deles:
-10x³ + 2x² – x – 12x³ – 9x – 3x² – x =
Em seguida, é só separar os termos que são semelhantes e resolver:
-10x³ – 12x³ + 2x² – 3x² – x – 9x – x =
-22x³ – x² – 11x =
Não esqueça que somamos números com o mesmo sinal e o sinal permanece no resultado, como, ![]()
Subtraímos números com sinais diferentes e o resultado fica o sinal do algarismo maior, como fizemos na expressão: 2x² – 3x² = -x².
Resumo sobre polinômios
Veja a aula do professor Sérgio Sarkis, do nosso canal do Curso Enem Gratuito, para entender melhor a definição de polinômio:
Multiplicação
Nesta operação, multiplicamos termo a termo e temos que ter cuidado com os expoentes.
Na multiplicação aplicamos a Propriedade de Potências de mesma Base onde conservamos a base e somamos os expoentes. Esse princípio é representado pela seguinte expressão:
am x an = am+n
Vamos aprender a multiplicar passo a passo.
Monômio por Polinômio
Vejamos essa operação através de um exemplo:
Multiplicamos cada termo do polinômio pelo monômio que está fora dos parênteses, coeficiente com coeficiente:
15w . (6w² – 8wx + x³) = 15w . 6w² – 15w . 8wx + 15w . x³
Aplicamos a propriedade de potências de mesma base:
90w1+2 – 120w1+1x + 15wx³ =
90w³ – 120w²x + 15wx³
E está pronto!
Polinômio por Polinômio
Usamos ou método acima para esse tipo de multiplicação também! Veja:
(a + b + c) . (2a – 2b – c) =
Multiplicamos termos a termo:
(a + b +c) . (2a – 2b – c) = 2aa – 2ab – ac + 2ab – 2bb – bc + 2ac – 2bc – cc
Aplicamos a propriedade de potências de mesma base:
(a + b +c) . (2a – 2b – c) = 2a² – 2ab – ac + 2ab – 2b² – bc + 2ac – 2bc – c²
Os termos que têm sinais opostos e mesmo coeficiente (número) e parte literal devem ser anulados. Já nos outros termos, fazemos as operações normalmente e está resolvido:
(a + b + c) . (2a – 2b – c) = 2a² – 2b² + ac – 3bc – c²
Resumo das operações com polinômios
Assista a mais esta aula sobre adição, subtração e multiplicação de polinômios! Quem ensina é o professor Sarkis, de Matemática.
Divisão
Na divisão com polinômios precisamos também aplicar uma propriedade de potência: Quociente de potências de mesma base, onde “conservamos a base e subtraímos os expoentes”. Veja como fica a expressão na linguagem matemática:
am ÷ an = am-n
Agora, que você já sabe o que tem que fazer, vamos ilustrar as divisões com exemplos práticos.
Divisão de monômio por monômio
Essa divisão é simples pois dividimos os coeficientes e aplicamos a propriedade de quociente de potências de mesma base. Veja exemplo:
10a¹² ÷ 2a³ = (10/2)a12-3 = 5a9
Divisão polinômios por monômios
Dividimos termo a termo do polinômio pelo monômio, usando a propriedade de quociente de mesma base:
![]()
Para melhor compreensão representamos a divisão através da fração.
Dividimos os coeficientes que estão coloridos em primeiro lugar:
![]()
Agora, subtraímos os expoentes das bases iguais:
(30w10 + 25w8 – 20w4) ÷ (5w4) = 6w10-4 + 5w8-4 – 4w4-4
(30w10 + 25w8 – 20w4) ÷ (5w4) = 6w6 + 5w4 – 4w0
No resultado ainda surgiu uma outra propriedade da Potência que é “toda base elevada ao expoente zero tem a sua potência igual a 1”:
-4w0 = -4(1)
Então temos o resultado da divisão:
(30w10 + 25w8 – 20w4) ÷ (5w4) = 6w6 + 5w4 – 4
Nosso objetivo em escrever esse artigo foi mostrar as principais operações utilizando Polinômios. Espero que com esta aula você fortaleça sua base matemática para desvendar as situações-problema apresentadas em provas de vestibular e Enem.
Resumo sobre divisão de polinômios
Aprenda a fazer a divisão de polinômios na prática com a videoaula a seguir:
Exercícios sobre operações com polinômios
Para terminar, resolva os exercícios sobre operações com polinômios a seguir, selecionados pela professora Wania.
1- (Uel)
O polinômio p tem grau 4n+2 e o polinômio q tem grau 3n-1, sendo n inteiro e positivo. O grau do polinômio p.q é sempre
a) igual ao máximo divisor comum entre 4n + 2 e 3n -1.
b) igual a 7n + 1.
c) inferior a 7n + 1.
d) igual a 12n² + 2n + 2.
e) inferior a 12n² + 2n + 2.
2)(ENEM – 2012)
As curvas de oferta e de demanda de um produto representam, respectivamente, as quantidades que vendedores e consumidores estão dispostos a comercializar em função do preço do produto. Em alguns casos, essas curvas podem ser representadas por retas. Suponha que as quantidades de oferta e de demanda de um produto sejam, respectivamente, representadas pelas equações:
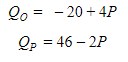
em que QO é quantidade de oferta, QD é a quantidade de demanda e P é o preço do produto.
A partir dessas equações, de oferta e de demanda, os economistas encontram o preço de equilíbrio de mercado, ou seja, quando QO e QD se igualam.
Para a situação descrita, qual o valor do preço de equilíbrio?
a) 5
b) 11
c) 13
d) 23
e) 33
3- (Enem 2012)
A cerâmica possui a propriedade da contração, que consiste na evaporação da água existente em um conjunto ou bloco cerâmico submetido a uma determinada temperatura elevada: em seu lugar aparecendo “espaços vazios” que tendem a se aproximar. No lugar antes ocupado pela água vão ficando lacunas e, consequentemente, o conjunto tende a retrair-se. Considere que no processo de cozimento a cerâmica de argila sofra uma contração, em dimensões lineares, de 20%.
Disponível em: www.arq.ufsc.br. Acesso em: 30 mar. 2012 (adaptado).
Levando em consideração o processo de cozimento e a contração sofrida, o volume V de uma travessa de argila, de forma cúbica de aresta a, diminui para um valor que é:
a) 20% menor que V, uma vez que o volume do cubo é diretamente proporcional ao comprimento de seu lado.
b) 36% menor que V, porque a área da base diminui de a2 para (1 – 0,2)a².
c) 48,8% menor que V, porque o volume diminui de a3 para (0,8a)3.
d) 51,2% menor que V, porque cada lado diminui para 80% do comprimento original.
e) 60% menor que V, porque cada lado diminui 20%.
GABARITO:
1 – b; 2 – b; 3 – c.





