Como calcular probabilidade simples
O número de possibilidades de um evento acontecer é chamado de probabilidade. Veja o que você precisa aprender para resolver questões de probabilidade simples.
A probabilidade simples surgiu através dos jogos de azar. Isso mesmo: a sorte e o azar nem sempre são conceitos abstratos. Geralmente, se um evento tem maior número de possibilidades de acontecer, então a probabilidade que aconteça também é maior, logo, você terá mais “sorte” ao apostar nesse evento.
O que é probabilidade
Veja um resumo de introdução ao assunto com o professor Sérgio Sarkis.
Neste resumo você viu alguns exemplos básicos de como funciona a probabilidade. Veja de novo o vídeo se precisar para entender um pouco mais sobre o assunto.
O conceito de probabilidade está basicamente relacionado ao maior ou menor número de possibilidades de um determinado evento acontecer. Então a probabilidade que aconteça o evento também pode ser maior ou menor. Nesta aula você vai entender um pouco mais o que significa o espaço amostral, a aleatoriedade dos eventos e como calcular resultados favoráveis dentro de uma gama de resultados possíveis.
Probabilidade simples
Para definir probabilidade basta você se perguntar quais as chances de algo que você quer que aconteça, de fato, acontecer. Por exemplo, se você está em um programa de auditório e tem que escolher entre 3 portas, qual a probabilidade de você escolher a porta premiada?
Bem, a solução intuitiva nos diz que dentre as 3 possibilidades de escolher a porta correta, você tem apenas uma. Logo, a probabilidade é de 1 em 3 chances. Mas como isso funciona matematicamente falando?
Primeiro, vamos dar nomes aos bois, ou melhor, aos nossos eventos. Sendo assim, temos:
- P(A): probabilidade de ocorrer um evento A;
- n(A): número de resultados favoráveis;
- n(Ω) (lê-se n de ômega): número total de resultados possíveis.
Assim, a probabilidade é determinada pela razão entre o número de eventos possíveis e o número de eventos favoráveis, e é dada pela expressão: ![]()
Logo, no exemplo das portas, a probabilidade P(A) de escolha correta é dada pelo número de resultados favoráveis (apenas 1) sobre o número total de resultados possíveis, assim:
PA = 1/3 = 0,333…
Este é um exemplo clássico no estudo das probabilidades, leia mais sobre o famoso problema de Monty-Hall que é um exemplo bacana de como a probabilidade funciona em contrapartida da intuição.
Espaço amostral
O espaço amostral é o espaço composto por todas as amostras/resultados possíveis de um experimento específico. É essencial saber qual o experimento para determinar seu espaço amostral.
Por exemplo: ao se lançar um dado de 6 lados aleatoriamente, temos um espaço amostral composto de 6 unidades de possibilidades: a possibilidade de cair na face 1, na face 2 e assim sucessivamente. Nesse caso, o espaço amostral é dado por:
S={1,2,3,4,5,6}
Tomemos o mesmo exemplo do dado para calcular um problema:
Exemplo: ao lançarmos um dado, qual a probabilidade de cair um número par?
No espaço amostral composto por todas as faces do dado, temos 3 possibilidades de cair um número par, sejam eles: 2, 4 e 6. Assim, temos: ![]()
Então, a probabilidade de cair um número par em um lançamento de dado aleatório é de 0,5 ou 50% de chance.
Importante: A probabilidade de um evento ocorrer é sempre um número entre 0 (probabilidade de evento impossível 0%) e 1 (probabilidade do evento certo 100%), dado por: 0 ≤ PA ≤1.
Está confuso sobre como transformar números decimais em porcentagem e vice-versa? Confere esta aula e tire todas suas dúvidas.
Tudo certo até aqui? Agora vamos ver um exemplo um pouco mais elaborado, para colocar em prática seus conhecimentos.
Exemplo de exercício
Exemplo 2: Em uma caixa há 4 bolas pretas, 6 bolas brancas e 8 bolas vermelhas. Retirando somente uma bola ao acaso, qual a probabilidade de ela ser preta ou branca?
Solução: Nesse caso, é preciso prestar atenção no espaço amostral, ele é dado pela soma de todas as bolas, logo 4+6+8=18.
Agora, se você pensar em partes, a probabilidade de a bola ser branca é 
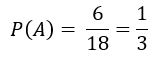
Por outro lado, a probabilidade de a bola ser preta é de 
![]()
Então, a probabilidade de a bolinha retirada da caixa ser preta ou branca é de 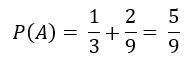
Logicamente falando, temos 4 bolas pretas e 6 bolas brancas totalizando um total de 10 bolas a serem retiradas de um montante de 18 bolas, logo, a probabilidade também pode ser dada por 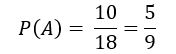
Exercícios sobre probabilidade
1 – (Faculdade Santo Agostinho BA/2017)
Cara ou Coroa é um jogo simples, que consiste em se atirar uma moeda ao ar para, então, verificar qual de seus lados ficou voltado para cima após sua queda. Segundo historiadores, O “Cara ou Coroa” já foi importante para resolver grandes impasses. Nos EUA, em 1845, Asa Lovejoy e Francis Pettygrove jogaram a moedinha para saber quem escolheria o nome da nova cidade do estado de Oregon. Pettygrove levou a melhor e nomeou a cidade como Portland.
Antes de iniciar o jogo, eles combinaram que:
– lançariam a moeda 5 vezes;
– considerariam como resultado a sequência formada pelas faces da moeda: cara ( K ) ou coroa ( C ).
De acordo com as regras combinadas, a probabilidade de que ocorresse uma sequência com 3 caras e 2 coroas era de
a) 7/32
b) 7/16
c) 5/32
d) 5/16
2 – (FPS PE/2019)
Uma clínica de angiologia atende 800 pacientes e 15% destes são amputados. Quarenta por cento dos pacientes da clínica são homens e um sexto das mulheres são amputadas. Se um paciente da clínica, escolhido aleatoriamente, não é amputado, qual a probabilidade desse paciente ser homem?
a) 5/17
b) 8/17
c) 6/17
d) 9/17
e) 7/17
3 – (UNCISAL/2019)
Em um programa de premiações, o participante tem a possibilidade de aumentar o valor do seu prêmio ao girar uma roda dividida em arcos de tamanhos diferentes. Na construção dessa roda, um círculo foi inicialmente dividido em 16 partes iguais e, depois, foram destacados alguns setores dessa divisão e a cada setor circular foi associado um número, conforme mostra a figura a seguir. A pontuação que o participante obterá será aquela do setor apontado pela seta no instante em que a roda parar de girar. Caso a seta aponte para exatamente a divisa entre dois setores, a roda deverá ser girada novamente.
Joana está participando desse programa e encontra-se em uma etapa da premiação na qual ela ganhará o valor do prêmio em dobro se fizer menos de 40 pontos ao girar a roda. A chance de Joana ganhar o prêmio em dobro é
a) alta, porque a probabilidade de isso acontecer é de 10/16.
b) alta, porque a probabilidade de isso acontecer é de 6/10.
c) média, porque a probabilidade de isso acontecer é de 9/16.
d) baixa, porque a probabilidade de isso acontecer é de 7/16.
e) baixa, porque a probabilidade de isso acontecer é de 4/10.
Gabarito:
- D
- E
- C





