Radiciação: propriedades, exemplos e exercícios
A radiciação tem origem geométrica e aritmética. Saiba mais sobre o tema nessa revisão de Matemática do Curso Enem Gratuito!
Nesta aula vamos revisar uma operação matemática que tem origem tanto na geometria como na aritmética: a radiciação. Estude com a gente, pois no Enem não dá pra perder tempo quebrando a cabeça com operações de matemática básica!
O que é radiciação
O estudo e operações com raízes surgem em nossas vidas de estudante quando começamos a resolver problemas mais complexos envolvendo a aritmética e a geometria, certo? Quando falamos em radiciação não tem como fugirmos dos termos raiz quadrada, raiz cúbica, índice da raiz, símbolo da raiz, radicando, operações e propriedades das raízes. E nessa aula vamos estudar tudo isso e mais.
Na aritmética aprendemos o conceito de radiciação como sendo a operação inversa da potenciação. Os seguintes exemplo geralmente são apresentados pelos professores de matemática:
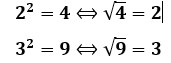
E assim apresentamos a raiz quadrada de um número, onde o índice da raiz quadrada é 2, mas o costume é não aparecer no sinal de raiz.
Mas a definição geral da Radiciação é:

Quando estudamos as primeiras raízes, usamos o que chamamos de quadrados perfeitos. Esses números independente de seu sinal tem uma raiz quadrada exata e em módulo, isto é, uma raiz de valor positivo. Veja os exemplos:

Existe uma propriedade que diz que um número elevado ao mesmo índice da raiz, o valor da raiz é o próprio módulo do número. Por isso os exemplos dos quadrados perfeitos são válidos.
Antes de ver como realizar operações envolvendo raízes, relembre como calcular a raiz quadrada com a videoaula do prof. Lucas:
Operações envolvendo raízes
Adição e Subtração
As raízes devem ter o mesmo índice e mesmo radicando, isto é, essas raízes devem ser idênticas.
Assim podemos adicionar ou subtrair seus coeficientes (números que vem a frente do sinal de raiz). Observe os seguintes exemplos:
Subtração: Diminuímos os coeficientes e conservamos a raiz quadrada de 5.

Observe que operamos somente com os coeficientes e as raízes continuam as mesmas.
Multiplicação e Divisão
As raízes devem ter somente o mesmo índice para que possamos multiplicar ou dividir seus radicandos. Veja o exemplo a seguir:
Multiplicação:

Multiplicamos os coeficientes, permanece o sinal de raiz e multiplicamos também dentro do sinal de raiz os radicandos.
Divisão:
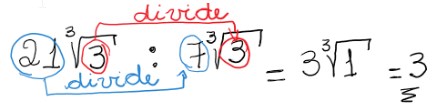
Dividimos os coeficientes. Dentro do sinal de raiz dividimos os radicandos e pronto!
Potência de um expoente
Esse caso é aquele que o radicando está elevado a um expoente, ou seja, em forma de potência. Nesse caso a raiz pode ser escrita em forma de potência com expoente fracionário. Exemplificando:
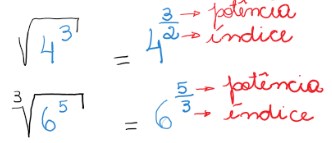
Note que o expoente da raiz tem o numerador como o expoente do radicando e o denominador é o índice da raiz. Essa propriedade é válida somente para radicandos positivos.
Propriedades da radiciação
Além das operações entre radicais/raízes temos ainda algumas propriedades importantes. Vamos conhecê-las?
1ª propriedade: simplificação de radicais
Se multiplicarmos ou dividirmos o índice da raiz e o expoente do radicando por um mesmo número Natural e diferente de zero, o resultado da raiz não se altera.
Vamos dar um exemplo usando a multiplicação:

2ª propriedade: produto de radicais de mesmo índice
Nesta multiplicação quando temos dois radicandos sendo multiplicados dentro de uma mesma raiz, podemos separá-los em duas raízes com o mesmo índice.
Olhe o exemplo:

3º propriedade: divisão de radicais de mesmo índice
Na divisão, podemos colocar os dois radicando sendo divididos no mesmo sinal de raiz se tiverem o mesmo índice. Veja nosso exemplo:
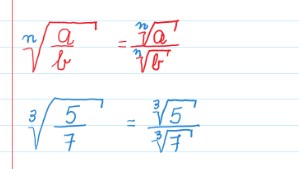
4ª propriedade: potência de uma raiz
Para elevarmos uma raiz a um expoente, basta elevar o radicando a esse expoente. Observe o exemplo:
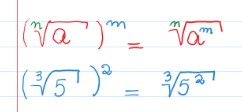
5ª propriedade: raiz de outra raiz
Para obtermos a raiz de outra raiz basta multiplicarmos os índices dessas raízes.
O exemplo mostra esse procedimento:
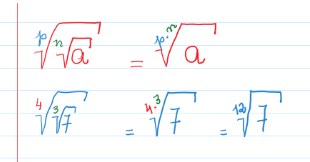
Conceito Geométrico da Radiciação
Como afirmamos no início dessa aula, a Radiciação tem sua origem da geometria. O símbolo da raiz quadrada surgiu para representar o cálculo do lado de um quadrado a partir de sua área.
O conceito da área de um quadrado é o produto do lado pelo lado, isto é lado ao quadrado:

O quadrado com lado l tem área:

Com um exemplo vai ficar tudo mais claro. Vamos a ele:

Agora você deve estar se perguntando se a raiz cúbica tem um significado geométrico também. É claro que sim!
O símbolo de raiz cúbica foi criado para calcular a aresta de um cubo a partir de seu volume. Observe onde é a aresta do cubo na figura abaixo:

Como gosto de exemplificar, vamos a uma aplicação sobre esse assunto:

Videoaula sobre radiciação
Quer saber mais? Assista ao nosso vídeo sobre o assunto:
Exercícios sobre radiciação
Sumário do Quiz
0 de 10 questões completadas
Perguntas:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
Information
.
Você já fez este questionário anteriormente. Portanto, não pode fazê-lo novamente.
Quiz is loading...
You must sign in or sign up to start the quiz.
Para iniciar este questionário, você precisa terminar, antes, este questionário:
Resultados
0 de 10 perguntas respondidas corretamente
Seu tempo:
Acabou o tempo
Você conseguiu 0 de 0 pontos possíveis (0)
| Pontuação média |
|
| Sua pontuação |
|
Categorias
- Sem categoria 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- Respondido
- Revisão
-
Pergunta 1 de 10
1. Pergunta
(PUC Campinas SP/ 2017)
Usando a tecnologia de uma calculadora pode-se calcular a divisão de 2 por
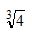 e obter um resultado igual aCorreto
e obter um resultado igual aCorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre radiciação para acertar na hora da prova!
-
Pergunta 2 de 10
2. Pergunta
(ESPM SP/ 2016)
A equação
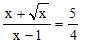 em que x é um número real apresenta:Correto
em que x é um número real apresenta:CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre radiciação para acertar na hora da prova!
-
Pergunta 3 de 10
3. Pergunta
(IFRS/2018)
Se
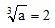 , então o valor da expressão
, então o valor da expressão 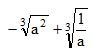 é:Correto
é:CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre radiciação para acertar na hora da prova!
-
Pergunta 4 de 10
4. Pergunta
(IFMA/ 2016)
Sobre os itens abaixo
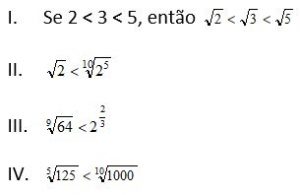
Podemos afirmar que:
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre radiciação para acertar na hora da prova!
-
Pergunta 5 de 10
5. Pergunta
(IFSC / 2015)
Leia e analise as seguintes afirmações:

Assinale a alternativa CORRETA.
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre radiciação para acertar na hora da prova!
-
Pergunta 6 de 10
6. Pergunta
(ESPM SP/2015)
O valor da expressão
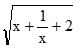 para x = 400 é igual a:Correto
para x = 400 é igual a:CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre radiciação para acertar na hora da prova!
-
Pergunta 7 de 10
7. Pergunta
(UNIFAP AP/ 2015)
Eles sabem que racionalizar é assunto do nono ano e não cai com frequência em provas, mas resolvem por via das dúvidas treinarem um pouco. E uma das questões que eles resolveram e acertaram é:
A fração
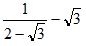 é igual a.
é igual a.Qual é a alternativa que eles marcaram:
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre radiciação para acertar na hora da prova!
-
Pergunta 8 de 10
8. Pergunta
(UNIRG TO/ 2014)
Uma pessoa, ao calcular 5% da metade da raiz quadrada de um número, encontra o valor 0,1. Nesse sentido, conclui-se que esse número é:
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre radiciação para acertar na hora da prova!
-
Pergunta 9 de 10
9. Pergunta
(PUC RJ/ 2013)
O valor de
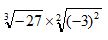 é:Correto
é:CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre radiciação para acertar na hora da prova!
-
Pergunta 10 de 10
10. Pergunta
(UNIFOR CE/2018)
Em um famoso programa de televisão de perguntas e respostas, a cada resposta correta para a pergunta feita, os participantes recebiam uma recompensa em dinheiro e passavam para a pergunta seguinte, com um grau de dificuldade mais elevado que a anterior. Uma das perguntas feitas a um participante foi a seguinte: “A um número n acrescentam-se cinco unidades. Se a raiz cúbica desse número é –1, qual é o valor de n? ”Sabendo que o participante respondeu corretamente, a resposta dada por ele foi
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre radiciação para acertar na hora da prova!
Referências:
MORAES, J. L. de. Matemática e Lógica para Concursos. São Paulo: Saraiva, 2013

Sobre o(a) autor(a):
Wania Maria de A. Pereira - A professora Wania Maria de A. Pereira é graduada em Física e Matemática pela Universidade Federal de Santa Maria (UFSM) e é Psicopedagoga com enfoque em Gestão de Pessoas (UNC) e especialista em Educação a Distância (SENAC- SC). Atuou na rede particular, estadual e municipal por 26 anos no Estado de Santa Catarina. Autora de diversos materiais didáticos para universidades públicas e privadas na área de Matemática, Metodologia de Ensino de Matemática e Psicopedagogia. Atualmente trabalha na área de Projetos de Tecnologias Digitais de Informação e Comunicação (TDICs). LinkedIn: https://www.linkedin.com/in/wmariaap/.
Gostou? Compartilhe!
Continue lendo:
Aqui vão 2 publicações relacionadas que talvez você goste:

Como resolver a prova de Matemática no Enem 2024? Veja as dicas do professor
Por Melina Zanotto | 08 de novembro
Confira as orientações e estratégias do professor Lucas Borguezan para se sair bem na prova de Matemática no Enem 2024.

Aulão Enem de Matemática: revisão intensiva e gratuita para a prova
Por João Vianney dos Valles Santos | 11 de outubro
Assista ao Aulão Enem de Matemática do Curso Enem Gratuito e revise os conteúdos mais importantes para a prova.


