Círculo e Circunferência: resumo com simulado de Matemática

(UECE/2019)

Em um plano munido com o sistema de coordenadas cartesianas usual, fixada uma unidade de comprimento (u.c), a equação x² + y² + 2x – 2y + 1 = 0 representa uma circunferência com centro no ponto P(p,q) cuja medida do raio é r u.c. Assim, é correto afirmar que o valor da soma p + q + r é igual a

(UNIOESTE PR/2019)

Considere as equações y = 4x – 5 e y = x² – 5x + 3. Suponha que os pares ordenados (x₁, y₁) e (x₂, y₂) satisfaçam as duas equações e que x₁ < x₂. Suponha ainda que o par (4, y₃) satisfaça somente a primeira equação. Então é CORRETO afirmar que a equação da circunferência, que tem centro em (4, y₃) e que passa pelo ponto (x₂, y₂), é dada por

(UNICAMP SP/2019)

No plano cartesiano, considere a circunferência de equação x² + y² – 4y + 3 = 0 e a parábola de equação 3x² – y + 1 = 0. Essas duas curvas se interceptam em

(FGV /2018)    

No plano cartesiano, uma circunferência passa pelos pontos (–1, 1) e (2, 2). Sabendo que o centro da circunferência pertence à reta y = 3x, pode-se concluir que a soma das coordenadas do centro é:

(ENEM/2018)

Um jogo pedagógico utiliza-se de uma interface algébrico-geométrica do seguinte modo: os alunos devem eliminar os pontos do plano cartesiano dando “tiros”, seguindo trajetórias que devem passar pelos pontos escolhidos. Para dar os tiros, o aluno deve escrever em uma janela do programa a equação cartesiana de uma reta ou de uma circunferência que passa pelos pontos e pela origem do sistema de coordenadas. Se o tiro for dado por meio da equação da circunferência, cada ponto diferente da origem que for atingido vale 2 pontos. Se o tiro for dado por meio da equação de uma reta, cada ponto diferente da origem que for atingido vale 1 ponto. Em uma situação de jogo, ainda restam os seguintes pontos para serem eliminados: A(0 ; 4), B(4 ; 4), C(4 ; 0), D(2 ; 2) e E(0 ; 2).

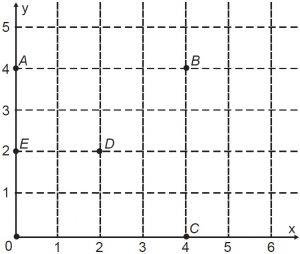
Passando pelo ponto A, qual equação fornecia a maior pontuação?

(UEFS BA/2018)

Uma circunferência de equação x2 + y2 + 5x + 2y – 24 = 0 intercepta os eixos coordenados determinando os vértices de um quadrilátero, conforme a figura.

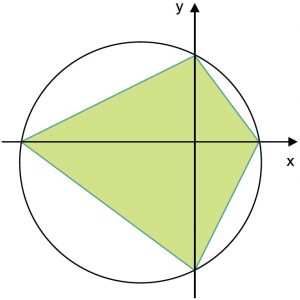
A área desse quadrilátero é

(Mackenzie SP/2017)

Duas pessoas patinam sobre o gelo descrevendo trajetórias circulares. As circunferências descritas por elas são dadas pelas equações

(x + 3)² + (y + 1)² = 10 e (x + 3)² + y² = 13, respectivamente. A distância entre os dois pontos de interseção das circunferências é

(UNCISAL/2017)

Um projeto de atividades extraclasse de uma escola reuniu as disciplinas Filosofia, definindo o tema (Promoção da Felicidade), Português, estabelecendo o slogan (Seja mais feliz: sorria sempre) e Matemática. O símbolo da campanha, que foi definido através de um concurso junto ao alunado, previa sua construção com a utilização apenas de gráficos de funções e figuras planas. A figura apresenta o símbolo vencedor, que foi concebido com três circunferências (uma representando o rosto e duas representando os olhos) e partes de duas parábolas definindo a boca, aberta num longo sorriso.

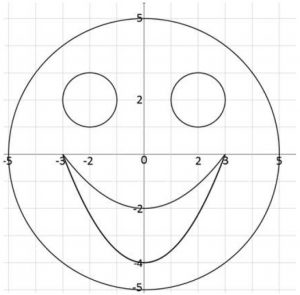
As expressões matemáticas utilizadas para desenhar o rosto, o olho direito e o lábio superior, foram, respectivamente,

(UNICESUMAR PR/2017)

Uma circunferência  passa pelo ponto P(4, 4) e tem seu centro sobre a reta de equação y = 2x. Uma reta t passa pelo ponto Q(2, 9) e é tangente à circunferência no ponto P. A ordenada do centro dessa circunferência vale

(USF SP/2017)

No sistema de coordenadas cartesianas, a reta r passa pela origem do sistema e pelo centro da circunferência de equação 2x² + 2y² – 16x – 12y + 18 = 0. A equação da reta s, que é paralela à reta r e que passa pelo ponto (–1, –3), é