Aprenda a resolver Função de 1º grau. Matemática básica
Aprenda a interpretar os gráficos e resolver exercícios básicos de Funções Afins (Função de 1º grau). Todo ano cai nas provas do Enem e dos vestibulares. Veja agora:
A Função de 1º grau ou Função Afim é a função das retas inclinadas e que aparecem muito em Física (como no estudo dos Movimentos Retilíneos e seus gráficos) assim como na análise de gráficos de Química, Biologia e Tratamento da Informação.
Nessa aula vamos ensinar de forma resumida o estudo da Função Afim ou de 1º grau e o estudo do gráfico dessa função.
Sabemos que a função de 1º grau é representada pela forma:
![]() Você faz leitura assim: “Efe de xis é igual a axis mais bê.
Você faz leitura assim: “Efe de xis é igual a axis mais bê.
Onde
![]()
![]() é o termo independente. Também é um número real de qualquer valor.
é o termo independente. Também é um número real de qualquer valor.
E lembramos também que a notação ![]()
Introdução à Função Afim: Função de 1º grau
Confira com o professor Lucas Borguezan, do canal do Curso Enem Gratuito, os fundamentos para você dominar os conceitos das Funções de 1º grau, também chamadas de Funçoes Afins.
Vamos ilustrar agora o que você aprendeu com esses conceitos com alguns exemplos:

Perceba que no último exemplo temos uma função com o termo independente igual a zero. Essa função tem um nome especial e é chamada de Função Linear, que é um caso especial da Função Afim.
É importante que você lembre também que a Função de 1º grau tem seu Domínio e Imagem infinitos, pois admite quaisquer números reais.
Não lembra o que são Domínio e Imagem? Então, dá uma paradinha nessa aula e relembre estes termos neste post com os principais conceitos de funções.
Estudo do gráfico de uma Função de 1º grau:
O gráfico da função representada pela lei de formação: ![]() é uma reta oblíqua aos eixos 0x e 0y.
é uma reta oblíqua aos eixos 0x e 0y.
O que quer dizer isso? Que quando usamos uma função afim para descrever qualquer situação o gráfico é uma reta inclinada aos eixos x e y do plano cartesiano.
Para construir um gráfico precisamos de alguns itens importantes. São eles:
- Uma função,
- Uma tabela,
- Calcular no mínimo dois pontos (pares ordenados) para obtermos a reta.
Vamos utilizar o primeiro exemplo dado no início de nossos estudos:
![]()
Agora que escolhemos a função, vamos construir a tabela. Colocamos na primeira coluna valores de x, na segunda coluna a função que usaremos para calcular o valor de y e na última coluna os valores dos pares ordenados obtidos.
Os valores de x são escolhidos por nós, vamos usar os valores abaixo por serem mais simples para nosso cálculo.
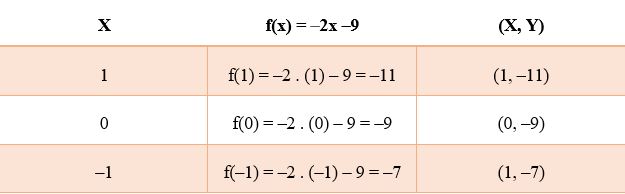
Você deve perceber que sempre substituímos os valores de x na função para obtermos os valores de y.
Agora que obtivemos os valores dos pares ordenados, basta situá-los nos eixos.
Como resolver Funções de 1º grau:
Comece pelo novo resumo do professor Lucas, agora com a resolução de problemas de Função Afim, para você aprender e gabaritar nas questões das provas.
Exercício resolvido
Vamos utilizar papel quadriculado e canetinhas para que você entenda melhor e também poder repetir os passos para estudar as funções de 1º grau:
– Primeiro traçamos os eixos x e y.
– Depois colocamos os valores de x que usamos na tabela no seu respectivo eixo. E, o mesmo fazemos com os valores de y. Veja:
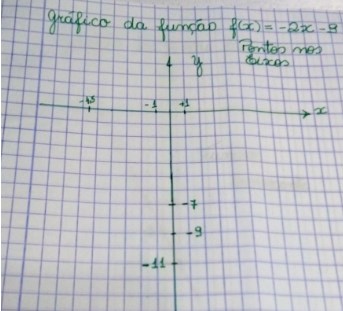
– Agora traçamos os pontilhados unindo os valores dos pares ordenados, isto é, ligamos o 1 ao -11, 0 ao -9 e o -1 ao – 7.
– Em seguida, colocamos os pontos onde os traçados se encontram.
– Depois, passamos uma reta sobre esses pontos e temos o seguinte gráfico. Observe a foto:
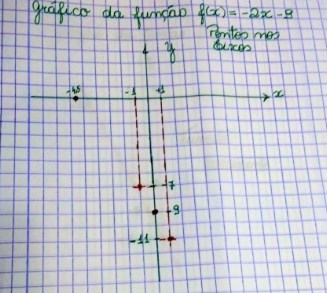
Agora basta unir os pontos e temos o gráfico pronto.
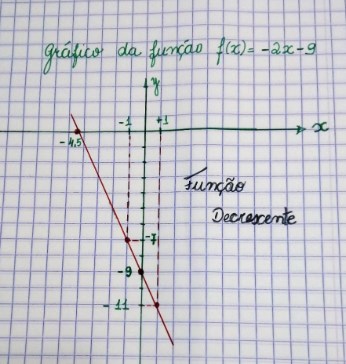
O que podemos concluir a partir desse gráfico?
1. A função ![]() é chamada de equação da reta r.
é chamada de equação da reta r.
2. O coeficiente ![]() é denominado de coeficiente angular da reta. Ele é que dá a inclinação dessa reta.
é denominado de coeficiente angular da reta. Ele é que dá a inclinação dessa reta.
3. E ![]() é chamado de coeficiente linear da reta e é o local que a reta corta o eixo y.
é chamado de coeficiente linear da reta e é o local que a reta corta o eixo y.
Tem a mais uma coisa! A partir de um gráfico podemos ainda calcular a raiz ou zero da função: basta fazer ![]()
Vamos calcular esse valor:
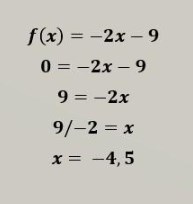
Esse ponto nos dá a localização do ponto onde a reta cortará o eixo x.
Com a análise desse gráfico podemos resumir as características de gerais para o gráfico de uma função qualquer através de algumas pequenas regras:

Não esqueça dessas regras! Com elas você conseguirá com certeza resolver qualquer situação problema que envolva a interpretação de gráficos de uma função de 1º grau.
Videoaula de resumo sobre Funções
Exercícios sobre função de 1º grau:
Sumário do Quiz
0 de 10 questões completadas
Perguntas:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
Information
.
Você já fez este questionário anteriormente. Portanto, não pode fazê-lo novamente.
Quiz is loading...
You must sign in or sign up to start the quiz.
Para iniciar este questionário, você precisa terminar, antes, este questionário:
Resultados
0 de 10 perguntas respondidas corretamente
Seu tempo:
Acabou o tempo
Você conseguiu 0 de 0 pontos possíveis (0)
| Pontuação média |
|
| Sua pontuação |
|
Categorias
- Sem categoria 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- Respondido
- Revisão
-
Pergunta 1 de 10
1. Pergunta
(UNCISAL/2019)
A empresa onde Antônio trabalha contratou uma instituição que oferece planos de saúde. De acordo com o contrato, o valor da mensalidade I(r) a ser pago pelos empregados ao plano de saúde está vinculado à renda mensal — r, em mil reais — de cada um deles, conforme a posição nos intervalos do eixo horizontal no gráfico a seguir. Para um empregado com renda inferior a R$ 5 000,00, a própria empresa custeará o plano de saúde. Para os demais, a mensalidade do plano seguirá os intervalos de valores indicados no gráfico, de modo que, por exemplo, 0,2r significa que a mensalidade do plano será igual à renda no intervalo correspondente multiplicada pelo fator 0,2.
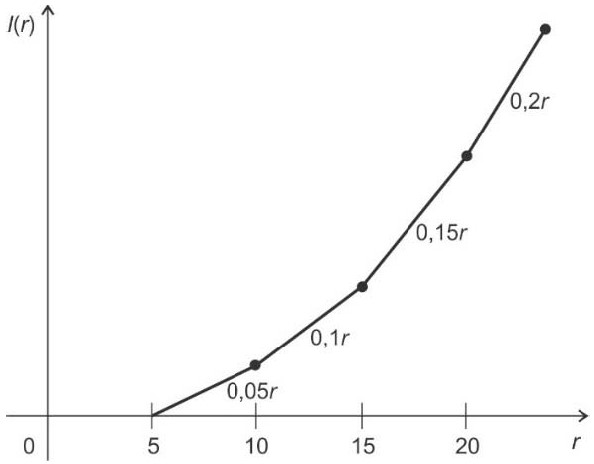
Se a renda mensal de Antônio é R$ 11 000,00, qual será o percentual que ele pagará pelo plano de saúde?
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre função de 1º grau para acertar na hora da prova!
-
Pergunta 2 de 10
2. Pergunta
(UERJ/2019)
A população de uma espécie animal fica multiplicada pelo mesmo fator após intervalos de tempo iguais. No período de 1984 a 1996, essa população passou de 12500 para 25000 indivíduos. Considere que, para o mesmo intervalo de tempo nos anos seguintes, o fator permanece constante.
O número de indivíduos dessa população em 2032 será aproximadamente igual a:
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre função de 1º grau para acertar na hora da prova!
-
Pergunta 3 de 10
3. Pergunta
(UNIFOR CE/2019)
Uma distribuidora de alimentos funciona de segunda à sexta-feira das 08:00 às 18:00. Às 8h de segunda-feira, a empresa tinha em seu estoque 42 toneladas de alimentos. Nesse dia, a empresa enviou 8 toneladas e recebeu 5. Na terça-feira, enviou 12 toneladas e não recebeu carregamento algum. Na quarta-feira, enviou 9 toneladas e recebeu 15. Na quinta-feira, enviou 8 toneladas e recebeu 11. Na sexta-feira, enviou 3 toneladas e recebeu 7. Qual dos gráficos representa a quantidade de alimentos (em toneladas) no estoque da empresa no final de cada dia?
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre função de 1º grau para acertar na hora da prova!
-
Pergunta 4 de 10
4. Pergunta
(UERJ/2018)
Os veículos para transporte de passageiros em determinado município têm vida útil que varia entre 4 e 6 anos, dependendo do tipo de veículo. Nos gráficos está representada a desvalorização de quatro desses veículos ao longo dos anos, a partir de sua compra na fábrica.
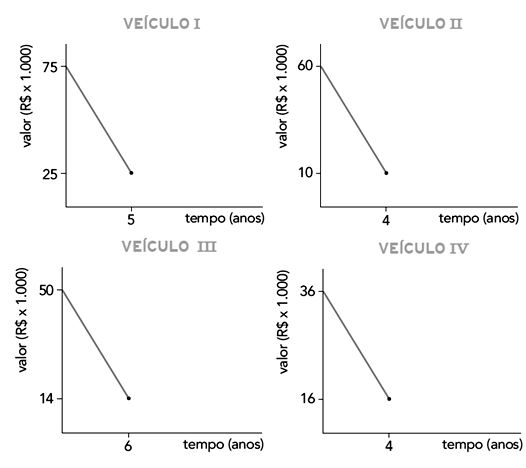
Com base nos gráficos, o veículo que mais desvalorizou por ano foi:
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre função de 1º grau para acertar na hora da prova!
-
Pergunta 5 de 10
5. Pergunta
(FATEC SP/2018)
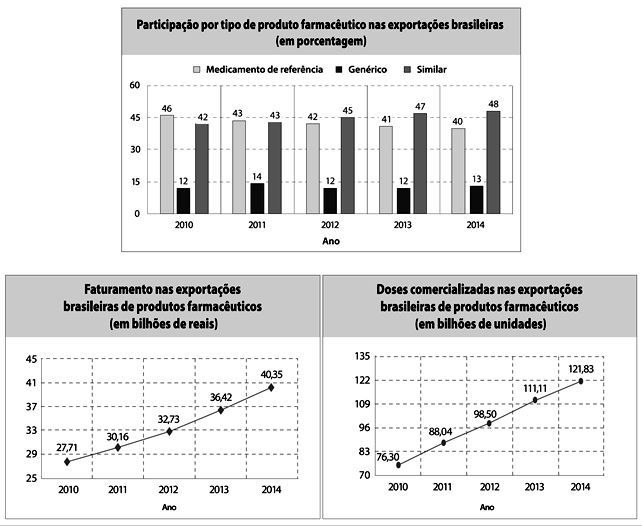
<https://tinyurl.com/yaevl4u9> Acesso em: 25.02.2018. Adaptado. No período de 2010 a 2014, o crescimento no número de doses comercializadas, em bilhões de unidades, é aproximadamente linear.
Se o crescimento observado de 2010 a 2014 se mantiver nos próximos anos, o número de doses comercializadas em 2018, em bilhões de unidades, será, aproximadamente,
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre função de 1º grau para acertar na hora da prova!
-
Pergunta 6 de 10
6. Pergunta
(UNITAU SP/2018)
Em um determinado estado brasileiro, no final de 2012, o número de pessoas infectadas pela febre amarela era igual a 324 e, no final de 2017, esse número passou para 859 pessoas. Admitindo que o número de pessoas infectadas cresce linearmente com o tempo, podemos afirmar que, no final de 2018, o número de pessoas infectadas será igual a
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre função de 1º grau para acertar na hora da prova!
-
Pergunta 7 de 10
7. Pergunta
(UNICESUMAR PR/2018)
Seja f uma função de R em R, sendo R o conjunto dos números reais, definida por f(x) = 2x – 13, os valores de x pertencentes ao domínio dessa função e que produzem imagens maiores que 7 são tais que
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre função de 1º grau para acertar na hora da prova!
-
Pergunta 8 de 10
8. Pergunta
(UEG GO/2018)
A função que descreve o lucro mensal L de um comerciante, em função da quantidade x de produtos vendidos mensalmente, é representada pelo gráfico a seguir.
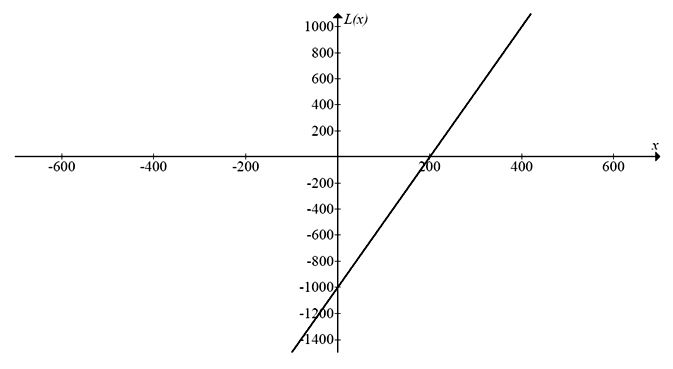
Analisando-se o gráfico, a quantidade de produtos que esse comerciante tem que vender para obter um lucro de exatamente R$ 2.000,00 é de
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre função de 1º grau para acertar na hora da prova!
-
Pergunta 9 de 10
9. Pergunta
(UFGD MS/2018)
Uma pesquisa sobre o Panorama dos Resíduos Sólidos no Brasil no ano de 2014, realizada pela Abrelpe (Associação Brasileira de Empresas de Limpeza Pública e Resíduos Especiais), apontou que os 467 municípios dos três estados da região Centro-Oeste e o Distrito Federal geraram, em 2014, a quantidade de 16.948 toneladas/dia de RSU (Resíduos Sólidos Urbanos), das quais 93,4% foram coletadas. Os dados indicam um crescimento de 2,2% no total coletado e um aumento de 1,9% na geração de RSU em relação ao ano anterior. A tabela a seguir apresenta os dados coletados e gerados de RSU no estado de Mato Grosso do Sul.
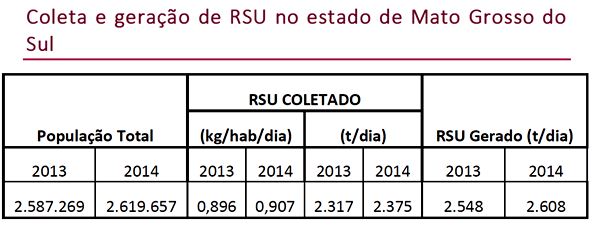
Fonte: Pesquisa ABRELPE e IBGE. Disponível em http://www.abrelpe.org.br/Panorama/panorama2014.pdf . Acesso em: 14 out. 2017 Supondo que a quantidade de RSU gerada no MS em t/dia seja uma função afim, é correto afirmar que a previsão de RSU a ser gerada em 2020 em t/dia será de
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre função de 1º grau para acertar na hora da prova!
-
Pergunta 10 de 10
10. Pergunta
(UFRGS/2018)
Para produzir determinado tipo de tecido, uma fábrica gasta R$ 2,20 por metro. Além disso, há uma despesa fixa de R$ 2.500,00, independente da quantidade de metros produzidos. Se cada metro do tecido é vendido por R$ 4,00, o número mínimo de metros no qual a fábrica passa a ter lucro com a venda é
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre função de 1º grau para acertar na hora da prova!

Sobre o(a) autor(a):
Wania Maria de A. Pereira - A professora Wania Maria de A. Pereira é graduada em Física e Matemática pela Universidade Federal de Santa Maria (UFSM) e é Psicopedagoga com enfoque em Gestão de Pessoas (UNC) e especialista em Educação a Distância (SENAC- SC). Atuou na rede particular, estadual e municipal por 26 anos no Estado de Santa Catarina. Autora de diversos materiais didáticos para universidades públicas e privadas na área de Matemática, Metodologia de Ensino de Matemática e Psicopedagogia. Atualmente trabalha na área de Projetos de Tecnologias Digitais de Informação e Comunicação (TDICs). LinkedIn: https://www.linkedin.com/in/wmariaap/.
Gostou? Compartilhe!
Continue lendo:
Aqui vão 2 publicações relacionadas que talvez você goste:

Como resolver a prova de Matemática no Enem 2024? Veja as dicas do professor
Por Melina Zanotto | 08 de novembro
Confira as orientações e estratégias do professor Lucas Borguezan para se sair bem na prova de Matemática no Enem 2024.

Aulão Enem de Matemática: revisão intensiva e gratuita para a prova
Por João Vianney dos Valles Santos | 11 de outubro
Assista ao Aulão Enem de Matemática do Curso Enem Gratuito e revise os conteúdos mais importantes para a prova.


