Domine agora o que é uma Função. Aprenda como resolver as questões que mais caem na Matemática do Enem, e confira também o que é e como funciona o Plano Cartesiano.
A função é bem explorada nos vestibulares e no Enem. Ela é apresentada de diversas formas e inserida em diversos assuntos como Estatística, Matemática Financeira, e em várias situações problemas em outras áreas de conhecimento como Física, Biologia e Geografia.
Vamos mostrar aqui os conceitos gerais mais importantes para o estudo da função: Domínio, Imagem e as principais funções reais.
O que é uma função?
Veja agora o que é uma Função com o professor Lucas Borguezan, do canal do Curso Enem Gratuito:
Ainda ficou difícil? Vou traduzir:
“Uma função é uma relação entre variáveis tais que a cada valor da variável de partida corresponde a apenas um valor na chegada e que pode ser expressa em diagramas, gráficos, tabelas ou equações.” (Fonte).
A variável de partida é conhecida como abscissa, geralmente é representada pela letra x e se encontra no eixo x de um plano cartesiano.
Já a variável de chegada é chamada de coordenada, é representada pela letra y e se encontra no eixo y de um plano cartesiano.
As duas variáveis de chegada e partida formam um único par ordenado (x,y). Lembramos que um par ordenado representa uma relação entre o eixo x e o y em um plano cartesiano. Veja Função por partes, que fic amais fácil entender:
Uma função só existe se num conjunto de pares ordenados (x, y) os valores de x são todos diferentes.
As funções podem representar fenômenos físicos, químicos, biológicos e estatísticos. Um exemplo bem conhecido da Física é a velocidade em função do tempo de um movimento retilíneo variado:
onde 
(velocidade em metros por segundo) e 
(tempo em segundos). Perceba que o valor da velocidade v depende exclusivamente do valor de t e este é representado no eixo x.
Veja o exemplo: Se queremos saber o valor da velocidade após 3 segundos de movimento, basta fazer
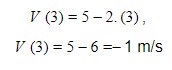
É claro que o valor da velocidade mudará se o valor que atribuirmos para o tempo mudar: para cada valor de tempo, teremos um novo valor de velocidade.
Dizemos que a principal característica de função é essa interdependência entre as variáveis, isto é, uma variável que depende de outra. Chamamos de:
- Variável independente: valor da variável do eixo x.
- Variável dependente: variável do eixo y.
Veja a imagem abaixo:
Figura 1 – Plano cartesiano e Par ordenado
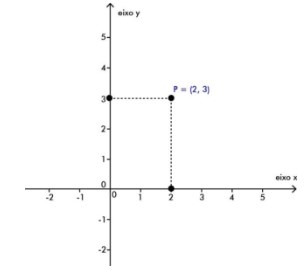
Perceba que:
O par ordenado é representado por P (2,3) onde o valor no eixo x é 2 e o valor do ponto no eixo y é 3.
O pontilhado no plano representa a correspondência entre os dois pontos das duas retas.
Resumo sobre o Plano Cartesiano
Confira agora com o professor Lucas Borguezan as dicas de Matemática Básica sobre o Plano Cartesiano:
Domínio e Imagem de uma função
Você já sabe que um par ordenado é composto de um valor de x (que é chamado de abscissa) e um valor de y (que tem o nome de ordenada). Portanto, podemos afirmar que o Domínio de uma função é o conjunto das ordenadas, isto é, dos valores de x. Já o conjunto Imagem de uma função é formado pelos valores das abscissas (valores de y).
Vamos determinar o Domínio e a Imagem da função: y = 3x. O Domínio dessa função são todos os valores de x pertencentes ao conjunto dos números reais R.
Já a Imagem dessa função é qualquer valor de y que corresponda a um valor de x. Nesse caso a Imagem é representada pelo triplo dos valores de x.
Então, segundo Leithold (2001), podemos descobrir o Domínio de uma função quando identificamos o conjunto de todos os valores de x que satisfazem essa função.
Para a função dada podemos descobrir os valores de y atribuindo valores a x.
Vamos colocar isso numa tabela:
Tabela 1 – Valores da função
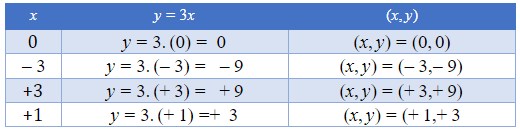
Observe que quando calculamos os valores na tabela também definimos a Imagem dessa função pois para cada valor de x obtivemos um valor de y. Então a Imagem da função é y = f(x). (Lemos função de x).
Mas o Domínio e a Imagem dessa função são iguais aos de outras?
Não. Existem vários tipos de função as Lineares, Quadráticas, Exponenciais, Logarítmicas entre muitas outras. E podem ser representadas de várias formas gráficas, algébricas ou diagramas. O comportamento do conjunto do Domínio e da Imagem dependem da forma e característica de cada tipo de função.
E reforce seu aprendizado!
Videoaula sobre funções
Para finalizar, assista à videoaula abaixo, com o professor Lucas, de Matemática, e aprenda funções de uma vez por todas!
Exercícios sobre funções
1) (ENEM – 2015)
Um meio de transporte coletivo que vem ganhando espaço no Brasil é a van, pois realiza, com relativo conforto e preço acessível, quase todos os tipos de transportes: escolar e urbano, intermunicipal e excursões em geral.
O dono de uma van, cuja capacidade máxima é de 15 passageiros, cobra para uma excursão até a capital de seu estado R$ 60,00 de cada passageiro. Se não atingir a capacidade máxima da van, cada passageiro pagará mais R$ 2,00 por lugar vago.
Sendo x o número de lugares vagos, a expressão que representa o valor arrecadado V(x), em reais, pelo dono da van, para uma viagem até a capital é
a) V(x) = 902x
b) V(x) = 930x
c) V(x) = 900 + 30x
d) V(x) = 60x + 2x²
e) V(x) = 900 – 30x – 2x²
2) (ENEM – 2015)
O sindicato de trabalhadores de uma empresa sugere que o piso salarial da classe seja de R$ 1 800,00, propondo um aumento percentual fixo por cada ano dedicado ao trabalho. A expressão que corresponde à proposta salarial (s), em função do tempo de serviço (t), em anos, é s(t) = 1 800 . (1,03)t.
De acordo com a proposta do sindicato, o salário de um profissional de empresa com 2 anos de tempo de serviço será, em reais,
a) 7 416,00.
b) 3 819,24.
c) 3 709,62.
d) 3 708,00.
e) 1 909,62.
3) (ENEM – 2014)
Um construtor precisa revestir o piso de uma sala retangular. Para essa tarefa, ele dispõe de dois tipos de cerâmicas:
a) cerâmica em forma de quadrado de lado 20 cm, que custa R$ 8,00 por unidade;
b) cerâmica em forma de triângulo retângulo isósceles de catetos com 20 cm, que custa R$ 6,00 por unidade.
A sala tem largura de 5 m e comprimento de 6 m.
O construtor deseja gastar a menor quantia possível com a compra de cerâmica. Sejam x o número de peças de cerâmica de forma quadrada e y o número de peças de cerâmica de forma triangular.
Isso significa, então, encontrar valores para x e y tais que 0,04x + 0,02y > 30 e que tornem o menor possível valor de
a) 8x + 6y .
b) 6x + 8y.
c) 0,32x + 0,12y.
d) 0,32x + 0,02y.
e) 0,04x + 0,12y.
Gabarito:
- E
- E
- A
