O que é Produto Cartesiano: resumo com exercícios
Você já deve estar craque em operações entre conjuntos não é mesmo? Mas aqui no Curso Enem Gratuito sempre tem algo a mais para você aprender. Vamos descobrir juntos?
Trabalhar com conjuntos na matemática parece algo bastante abstrato se você não fizer conexões com seu dia a dia. Mas, a parte sobre conjuntos é algo que você aprende no ensino fundamental e caminha contigo pelo resto da vida.
Hoje você vai aprender um pouquinho mais sobre o produto cartesiano, que pelo nome, parece não ter nenhuma ligação com as teorias de conjuntos.
Na verdade, o produto cartesiano pode ser visto como um tipo de operação entre conjuntos. Mas preste atenção! Não vale confundir o que é conjunto e o que é elemento!
Os Fundamentos do Produto Cartesiano – Veja agora com o professor Lucas Borguezan, do canal do Curso Enem Gratuito, uma introdução aos Conjuntos e Produto Cartesiano:
O que são os Elementos? O que é um Conjunto?
Então, “bora” distinguir essas palavrinhas matemáticas “Conjunto”, e “Elementos” umas das outras?
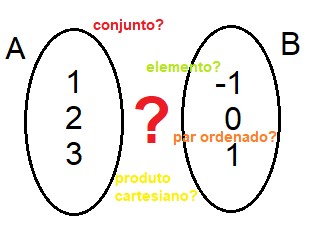
Produto Cartesiano e exemplos
Chamamos de produto cartesiano o conjunto de todas as possibilidades de relações entre os elementos do conjunto de partida e os elementos do conjunto de chegada. Ou seja, o produto cartesiano é o conjunto de todos os pares ordenados, cujo primeiro termo pertence a A e o segundo termo pertence a B.
Mas, quem são esses conjuntos de partida e de chegada? Vamos usar uma imagem para entender melhor.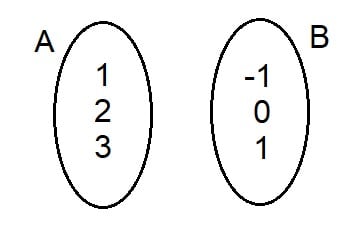
Consideramos o conjunto A como sendo A = {1, 2, 3} e o conjunto B = {-1, 0, 1}. Os três elementos do conjunto A podem se relacionar de diversas formas com os três elementos do conjunto B, e por isso vamos considerar o conjunto A como sendo o conjunto de partida e o conjunto B, o de chegada.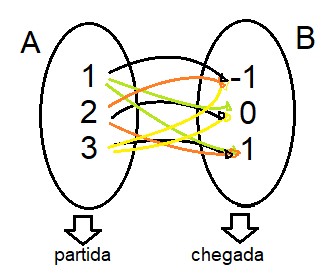
Todo esse emaranhado de relações pode ser expresso por extenso (imagine se fossem mais do que 3 elementos em cada conjunto, o tamanho da confusão), através de um novo conjunto, indicado por A x B, cujos elementos serão chamados de pares ordenados.
Esses pares ordenados são formados pelos elementos de A e de B, ou seja, o primeiro elemento pertence ao conjunto A e o segundo elemento pertence ao conjunto B.
Veja como exemplo, a relação dada pela primeira seta preta.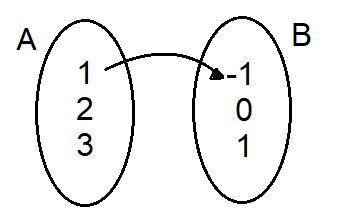
O par ordenado resultante desta relação é o (1,-1) onde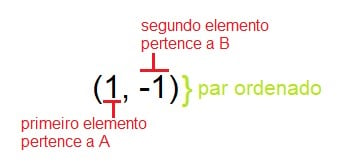
Então, se escrevermos um conjunto dado por A x B, onde todos os elementos são dados por pares ordenados que estabelecem uma relação entre os conjuntos A e B, temos:
A X B = { (1,-1) ; ( 1,0) ; (1,1) ; (2,-1) ; (2,1) ; (3,-1) ; (3,0) ; (3,1) }
O número de elementos dos conjuntos A e B pode ser expresso por n (A) e n (B). Como o conjunto A possui 3 elementos (n(A) = 3) e o conjunto B possui também 3 elementos (n(B) = 3) , o produto cartesiano A x B é um conjunto que possui 9 elementos ( n(A x B) =9), e esses elementos são os pares ordenados.
Importante: Perceba que mesmo levando o nome de produto, os elementos do conjunto A não são multiplicados pelos elementos do conjunto B, mas sim formam pares ordenados.
É imprescindível que você saiba qual a ordem em que aparecem os elementos dentro do par ordenado, pois isso é determinado por qual dos conjuntos é o conjunto de partida.
Veja, por exemplo, se invertêssemos a ordem, determinando o conjunto B como sendo o conjunto de partida e o conjunto A como sendo o conjunto de chegada.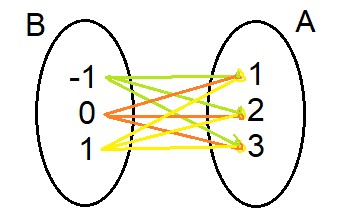
O produto cartesiano nesse caso seria dado por
B X A = { (-1,1) ; (-1,2) ; (-1,3) ; (0,1) ; (0,2) ; (0,3) ; (1,1) ; (1,2) ; (1,3) }
Note que os elementos (pares ordenados) do produto cartesiano A x B são diferentes dos elementos do produto cartesiano B x A.
Podemos representar um produto cartesiano através de um axioma, ele é escrito dessa forma:

Lê-se: o produto cartesiano de A x B é igual ao par ordenado (x, y) tal que x pertence ao conjunto A e y pertence ao conjunto B.
Exercícios de Conjuntos e Produto Cartesiano
Gostou dessa explicação? Que tal dar fazer uns exercícios para ter certeza que não restou dúvida alguma?
Questão 01)
Sejam os conjuntos:

Então o número de elementos do produto cartesiano  é igual a:
é igual a:
a) 2.
b) 4.
c) 6.
d) 8.
e) 9.
Gab: B
Questão 02)
Com os elementos (0,2), (1,4) (1,5) e (2,6), que são alguns dos elementos do produto cartesiano M x N, é possível determinar os conjuntos M e N. Com base nestes dados, assinale o que for correto.

Gab: 3.





