Teorema de Laplace e Regra de Chió no cálculo de matrizes
Saber os cálculos de matrizes de ordem superior é um pontinho garantido na hora da prova! Nesta aula você vai conhecer dois teoremas importantíssimos. Vem estudar pro Enem com a gente!
O Teorema de Laplace e a Regra de Chió são duas ferramentas imprescindíveis no estudo e manuseio das matrizes de ordem superior. Nesta aula você vai encontrar dicas e referências que farão você tirar de letra qualquer problema que envolva Laplace e Chió.
Preste atenção aos detalhes do resumo introdutório sobre Matrizes, e depois acompanhe as explicações do Teorema de Laplace e da Regra de Chicó. Ao final, resolva todos os exercícios para concluir a sua revisão.
O que são as Matrizes? – Veja agora uma introdução com o professor Lucas Borguezan:
O Teorema de Laplace
Menor complementar e cofator
Para compreender o teorema de Laplace, precisamos primeiro entender os conceitos de menor complementar e cofator. Vamos a eles:
Menor complementar (Dij)
Chamamos de menor complementar de um elemento de uma matriz o valor do determinante da matriz resultante ao eliminarmos a linha e a coluna a qual esse elemento pertence. Parece complicado assim só com palavras, não é mesmo? Então veja em um exemplo numérico como isso funciona:
Exemplo:
Seja a matriz A:
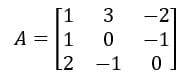
Qual é o menor complementar D23?
Bem, o menor complementar D23 está relacionado com o elemento a23 , ou seja, o elemento da segunda linha e terceira coluna:
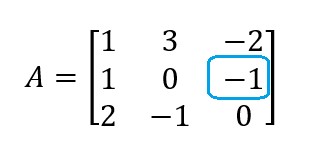
Agora, eliminamos a linha e a coluna a qual este elemento pertence, assim:

E montamos uma nova matriz com os elementos que “sobraram”, dessa forma:
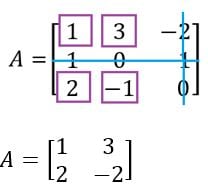
E calcula-se o determinante desta matriz, que equivale ao menor complementar D23:
det(A) = D23 = 1 . (-2) – 2 . 3 = -8
Cofator (Cij)
Para determinar o Cofator de um termo em uma matriz, basta utilizar a seguinte fórmula:

Na verdade, essa fórmula é bastante simples. O cofator nada mais é do que o próprio menor complementar. A posição linha e coluna do termo é que vai determinar se o menor complementar permanece com o mesmo valor ou se fica com valor negativo (essas são as duas únicas opções para -1 elevado a uma potência par ou ímpar).
Agora, vamos ver o que nos diz o teorema de Laplace, e verificar onde se encaixa o cofator.
Teorema de Laplace
Para calcular o determinante de uma matriz quadrada de ordem superior ou igual a 4 com o teorema de Laplace, basta escolher qualquer linha ou qualquer coluna da matriz e somar os produtos dos elementos dessa fila, pelos seus respectivos cofatores.
Exemplo: Calcule o determinante de

Bem, segundo o teorema, basta escolher qualquer linha ou coluna para calcular o determinante através dos cofatores. Uma estratégia que vale a pena ser utilizada é a de escolher a fila com maior quantidade de zeros, você logo verá o porquê.
Escolhemos, então, a coluna dois:
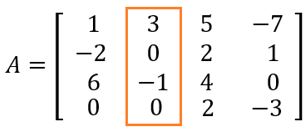
Agora, segundo o teorema, o determinante é dado pela soma dos produtos dos elementos dessa fila, pelos seus respectivos cofatores, sendo assim:
det(A) = 3 . C12 + 0 . C22 + (-1) . C23 + 0 . C42
Como zero multiplicado por qualquer número é zero, ficamos com:
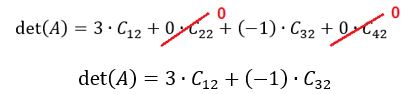
Assim, basta calcular os cofatores C12 e C23.
Utilizando a fórmula, temos:
C12 = (-1)1+2 . D12
Calculando o menor complementar D12:
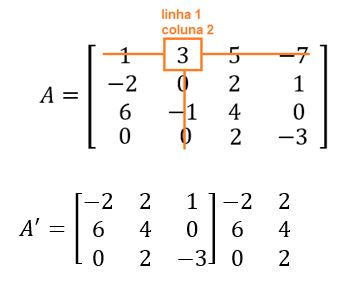
Aplicando Sarrus:
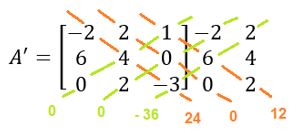
Temos:
det(A’) = 24 – 12 – (-36) = 72
Então:
C12 = (-1)1+2 . D12
C12 = (-1)1+2 . 72
C12 = -1 . 72
C12 = -72
Agora, calculamos o cofator C32. A fórmula diz que:
C32 = (-1)3+2 . D32
Calculando o menor complementar D32:
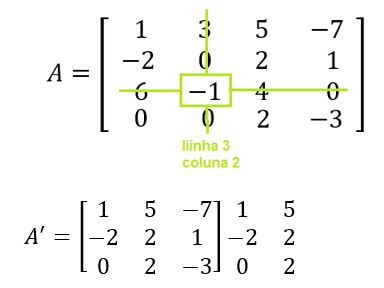
Aplicando Sarrus:
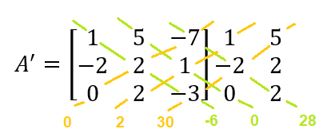
Temos det(A’) = 28 + (-6) – (30 + 2) = 22 – 32 = -10
Então, o cofator C32 tem valor igual a:
C32 = (-1)3+2 . -10
C32 = -1 . -10
C32 = 10
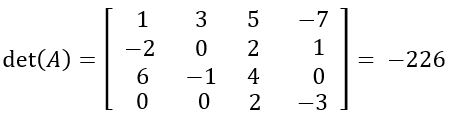
Depois de calculados os cofatores, voltamos para o cálculo do determinante de A, que nos diz que:
det(A) = 3 . C12 + (-1) . C32
Assim, substituindo os valores dos cofatores:
det(A) = 3 . -72 + (-1) . 10
det(A) = -216 – 10
det(A) = -226
Então, o valor do determinante da matriz
Entendeu por que é melhor escolher a fila com maior número de zeros? Quanto mais zeros, menos cofatores precisamos determinar e, assim, diminuímos a quantidade de cálculos.
O Cálculo de Área utilizando Matrizes
A Regra de Chió
Para calcular o valor do determinante de matrizes com ordem maior do que 3, podemos utilizar também a regra de Chió.
Essa regra permite construir uma matriz de ordem menor, ou seja, reduzir a ordem de uma matriz para uma matriz de ordem n-1, sendo possível, assim, calcular o determinante por meio de métodos já conhecidos como a regra de Sarrus.
Complicou na definição? Calma, vamos descomplicar geral na introdução do professor Lucas Borguezan, do canal do Curso Enem Gratuito:
A condição mais importante para a aplicação da regra de Chió é de que o primeiro elemento da matriz, o elemento a11, seja igual a 1.
Importante: caso o primeiro elemento da matriz não seja igual 1, utiliza-se o Teorema de Jacobi para “transformar” esse elemento em 1, veja no vídeo:
Você vai ver agora, a partir de um exemplo, como se dão os passos para reduzir a ordem da matriz, pela regra de Chió.
Exemplo: Calcule o determinante da matriz

O primeiro passo é verificar se o primeiro elemento (a11) é igual a 1.

Sendo assim, vamos suprimir a primeira fila e a primeira coluna, mas não apague! Os elementos nelas contidos serão utilizados nos cálculos posteriores.
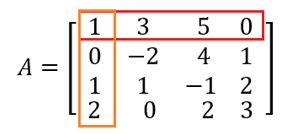
Agora, vamos reescrever uma nova matriz com os “elementos que sobraram”. Essa matriz será de ordem n – 1, nesse caso a ordem será 4 – 1 = 3.
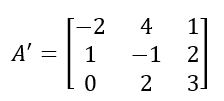
Preste atenção na próxima etapa, ela requer bastante cuidado.
Agora, a cada termo da nova matriz A’, iremos subtrair o produto dos termos suprimidos, ou seja, que se encontram à margem do elemento correspondente. Nesse caso, os elementos que se encontram à margem do -2 são os números 3 e 0, assim
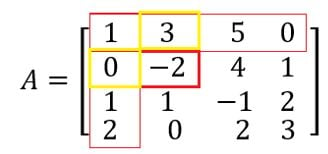
A matriz A’ fica da forma:
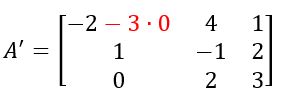
Já os elementos à margem do termo 4, são os termos, 5 e 0, logo:
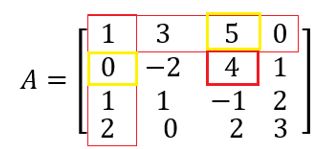
A matriz A’ fica da forma:

E assim sucessivamente.
Efetuando todos os cálculos, temos:
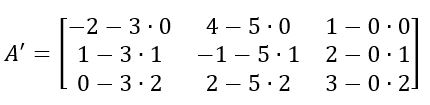
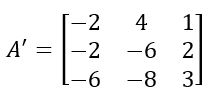
Agora, com uma matriz 3×3, podemos calcular o determinante usando técnicas já conhecidas, como a regra de Sarrus.
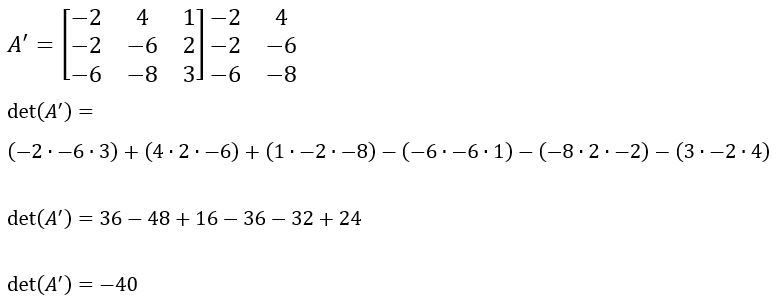
Então o determinante da matriz

É igual a det(A’) = -40.
Obs: Caso a matriz seja de ordem superior a 4, pode-se efetuar a regra de Chió sucessivas vezes, até chegar na matriz de ordem 3.
Exercícios envolvendo o Teorema de Laplace e a Regra de Chió
Questão 01)
Considere as matrizes
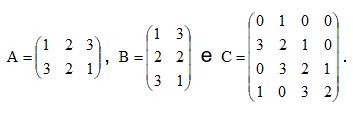
De acordo com conhecimentos sobre matrizes e determinantes, é incorreto afirmar que
1- det(MN) = det(NM), onde M e N são matrizes quadradas de mesma ordem.
2- detMt = –detM, onde M é matriz quadrada de ordem ímpar.
3- det(C) = 4.
4- a matriz AB possui três linhas e três colunas.
5- det(AB) = 96.
Questão 02)
A é uma matriz quadrada de ordem 4 e det A = -6. o valor de x tal que det (2A) = x – 97 é:
a) -12
b) zero
c) 1
d) 97/2
e) 194
Questão 03)
Dada uma matriz quadrada de ordem 4, cujo determinante é diferente de zero, quanto ao seu determinante. Marque V(verdadeiro) ou F(falso) para as alternativas abaixo
a) multiplicando uma linha de A por um escalar o seu determinante será k det (A).
b) multiplicando uma linha de A por um escalar o seu determinante será det (kA).
c) multiplicando a matriz A por um escalar o seu determinante será k det (A).
d) multiplicando a matriz A por um escalar o seu determinante será k2 det (A).
Gabarito:
- 5
- C
- VFFF





