A História nos diz muito sobre a origem da Matemática, dos números e suas simbologias. Aliás, você sabia que os símbolos matemáticos foram surgindo a partir da história da sociedade e de seu desenvolvimento? Vem entender essa relação no Curso Enem Gratuito!
Na área de Matemática existem diversos tipos de números com seus conceitos e características próprias. Os números negativos aparecem de certa forma quando estamos focados em temas como clima, finanças e esportes entre outros.
Nesta aula vamos revisar os principais conceitos que envolvem os números negativos, suas características como o uso do sinal negativo, débitos, quando são simétricos, a reta numérica, as quatro operações básicas e suas regras de sinais.
Vem com a gente revisar os números negativos para mandar bem em matemática!
Atualmente falamos muito em mudanças climáticas e a meteorologia nos dá uma ideia de como o clima vai se comportar. E, a maior preocupação em relação a esse assunto está relacionada às médias de temperaturas.
Uso dos números negativos
Em alguns lugares do planeta, é interessante que essas temperaturas permaneçam baixas e, para demonstrá-las, em geral usamos um sinal negativo em frente ao número e sua unidade, como – 1°C.
Em Urupema, cidade serrana de Santa Catarina, as médias de temperatura no inverno são bastante baixas. Como por exemplo, o dia 04 de junho de 2019, onde as temperaturas chegaram a – 1°C, possibilitando o surgimento de neve.
Perceba que o sinal negativo na frente do número 1 já te dá uma ideia de que está muito frio naquele determinado local, não é mesmo? Podemos dizer que está congelante!
Termômetros mostram temperaturas negativas. Legenda para cego ler: Foto mostra termômetro digital com temperatura de 1 grau negativo em uma paisagem serrana de Santa Catarina.
No setor de finanças temos outro exemplo onde os números negativos são úteis, especialmente quando tratamos de conceitos como débito e saldo. Quando fazemos uma compra em débito já sabemos que o dinheiro saiu de nossa conta, pois no extrato bancário há a um número negativo para representar o pagamento.
Isto é, se pagamos uma almoço de R$25,00 com cartão, esse dinheiro será descontado da conta. Teremos – 25 reais na conta. E quando a gente gasta demais e extrapola a quantidade de dinheiro que temos na conta?
Se temos limite no cheque especial, ficamos devendo para o banco. Esse débito é registrado em nosso extrato através de um número negativo.
Nos esportes, podemos perceber números negativos “traduzindo” diversos quesitos. Quando mergulhamos, por exemplo, podemos contar como referência o mar sendo nosso marco zero e, cada metro que mergulhamos, podemos representar como um “metro negativo” na nossa escala de referências.
Se você mergulhou 15 metros, por exemplo, podemos expressar isso como –15 metros.
Conjuntos numéricos
Existem muitos conjuntos numéricos, porém podemos afirmar que números só existem três tipos: positivos (+), zero (0) e negativos (–)
O zero é nosso ponto de referência, de equilíbrio e a partir dele podemos medir para sua direita ou para sua esquerda. Os números negativos e positivo podem ser simétricos.
Simétrico quer dizer que tem a mesma medida a partir do ponto zero.
Observe a reta numérica: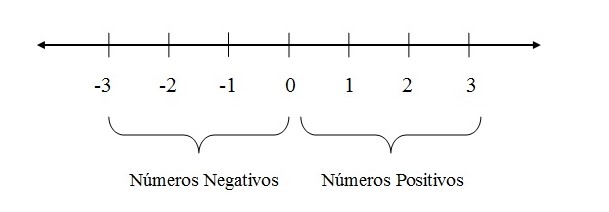
Figura 1 – Representação dos números positivos e negativos. Fonte: encurtador.com.br/rAF04. Legenda para cego ler: reta numérica com números negativos de-3 a-1, o zero e os números positivos de 1 a 3. Para mostrar que os números são simétricos.
Características dos números negativos
Nos textos e problematizações eles aparecem simbolizados por algumas palavras como débito, decréscimo, abaixo de, profundidade, perda, queda, desconto etc.
Assim se num enunciado aparecer números sem sinais, você vai identificar o sinal por palavras como as citadas acima.
Exemplos:
a) A Bolsa de valores teve uma queda de 20 por cento: – 20%.
b) A queda daquele homem foi de 15 metros. – 15 m.
c) A camisa custava R$ 120,00 e teve um desconto de R$ 50,00 porque paguei a vista:
120 – 50 =70.
Você compreende como é importante associar palavras com números? Esse é o conceito dos números negativos.
Comparando números negativos com os números positivos
Quando você quiser comparar dois números em termos de quantidade usamos os símbolos > ( maior), < (menor) ou igual.
No conjunto dos números Inteiros existem números negativos, o zero e os números positivos (que podem conter ou não um sinal de + antes do algarismo).
Na reta numérica, vimos que os números positivos de mesmo algarismo são simétricos, isto é sua distância até o número zero é a mesma.
Só que seus valores são diferentes, pois um número negativo é menor que um número positivo. Se compararmos alguns números da reta mais acima, usamos os símbolos de menor, maior ou igual. Veja os exemplos a seguir:
3 é maior que – 2, em linguagem matemática podemos dizer que 3 > – 2.
Para explicar esse pensamento matemático, usamos um exemplo sobre dinheiro pois é melhor ter 3 reais do que dever 2 reais. Dívidas sempre são simbolizadas com sinal negativo.
Outro exemplo:
– 1 é maior que – 3 ou – 1 > – 3, pois um número negativo é maior quando está mais próximo do zero na reta numérica.
Essa mesma expressão podemos escrever da forma inversa: – 3 é menor que – 1, isto é, – 3 < – 1.
Lembre muito bem dessa regra: quanto mais afastado o número negativo estiver do zero, na reta numérica, menor valor ele terá.
Operações com números negativos
a) Adição e Subtração:
Dizemos que existe uma regra de sinais para tudo em Matemática, porém nesse caso específico as pessoas se confundem ao resolver problema envolvendo números negativos.
Neste caso, a análise da resolução é o mais importante. Entenda que se somarmos duas dívidas essa dívida aumenta e não diminui.
Se o número negativo representa perdas, dívidas, decréscimos entre outros termos que já vimos, ele indica que houve sempre uma dívida.
Olhe o exemplo: Juan fez um empréstimo com o Banco de R$ 15 000,00. Não conseguiu pagar as prestações acordadas e fez outro empréstimo de 35 mil.
Juan está ganhando ou perdendo dinheiro? Sem contar os juros, correções e outras taxas, quanto Juan está devendo ao Banco agora?
– 15 – 35= – 45.
Você deve ter somado sem levar em conta o sinal, não é mesmo? Está correto. O sinal representa que esse rapaz está falido. Está com duas dívidas somadas.
A adição tem um conceito semelhante: Se você tem R$ 1 300,00 e gasta R$ 900,00, quanto que você ficará de saldo? 1300 – 900 = 400.
Mas, e se você recebeu o mesmo R$ 1300, 00 no mês e teve que comprar muitas coisas em seu cartão de crédito e a fatura veio com o valor de R$ 1500,00? Com certeza você vai gerar uma dívida de no mínimo:
1300 – 1500 = – 200.
Como a gente faz esse cálculo?
1500 – 1300 = 200, mas sabemos pelo exemplo que você ficou devendo, não é mesmo? Então temos que colocar o sinal negativo.
b) Multiplicação e Divisão
A multiplicação com números negativos é igual a multiplicação com números naturais, o que muda é a famosa regra de sinais.
Você deve ter aprendido que:
Se multiplicarmos números de mesmo sinal o produto entre eles tem sinal positivo.
Se multiplicarmos números de sinais diferentes o produto entre eles tem sinal negativo.
Aí vem aquela tabelinha que fica na cabeça da gente e queremos aplicar a tudo:
Regra de sinais da Multiplicação com números negativos. Legenda para cego ver: Tabela da regra de sinais da multiplicação com bordas vermelhas, três colunas e as duas colunas representam os fatores da multiplicação e a última o produto.Fonte: Elaborada pela autora (2020)
A aplicação dessas regras é muito mais simples do que somar ou subtrair números negativos, mas cuidado para não confundir as regras das operações.
A divisão se comportará da mesma forma que a multiplicação e, por isso usamos as mesmas regras e tabelas.
Vamos dar uns exemplos para que você relembre essas operações:
a) (– 15) . (+ 3) = – 45
b) ( – 18) . ( – 3) = + 54 = 54
c) ( – 144) : ( –12) = +12 = 12
Resumo sobre os números negativos.
Veja agora com o professor Lucas, do canal do Curso Enem Gratuito, uma introdução aos números negativos que vai ajudar geral na sua revisão completa.
Exercícios sobre números negativos:
1) (Garcia Gay, 2014 adaptado)
Denise precisa para R$ 480, 00 com seu cartão de débito, mas não sabe seu saldo no banco. Ao consultar seu extrato ela percebeu que:
– a dois dias atrás, se saldo era de 543 reais;
– Ontem, ela depositou um cheque de R$ 300,00 mas pagou contas com dois cheques: R$ 112, 00 e R$ 128,00.
O saldo bancário de Denise é expresso pela seguinte expressão?
a) 543 + ( 300 + 112 – 128).
b) 543 + 300 – (112 + 128)
c) 543 – ( 300 + 112 – 128).
d) 543 – 300 – (112 + 128).
e) 543 – 300 – (112 – 128).
2) Um mergulhador estava na superfície do mar e mergulhou 12 metros. Após alguns segundo desceu o triplo dessa profundidade. É correto afirmar que esse mergulhador desceu a uma profundidade de:
a) – 36
b) + 36
c) – 46
d) 48
e) – 48.
3) Um empresa num mesmo dia recebeu R$ 5.000,00 e teve despesas com material de escritório de R$ 3500,00 e manutenção de máquinas de R$ 1800,00. É correto afirmar que o saldo que essa empresa apresentou no final do dia foi de:
a) R$ 8 500,00.
b) R$ 6 700,00.
c) – R$ 300,00.
d) – R$ 700, 00.
e) – R$ 3300,00.
Gabarito:
1) b 2) e 3) c
Referências bibliográficas:
Giovanni Junior, José Ruy. Castrucci, Benedicto. A conquista da Matemática: 6º ano: ensino fundamental: anos finais – 4.ed. – São Paulo – FTD, 2018.
