Análise combinatória é um conjunto de métodos utilizados para contar possibilidades. Entenda o que é princípio aditivo e multiplicativo, e aprenda a utilizar fatoriais!
Análise combinatória é um tema que possui uma fama ruim nas escolas devido ao nome que carrega, já que, se você parar para pensar, se deparar com as palavras “análise” e “combinatória” realmente causa um estranhamento. O que é algo bastante contraditório, pois análise combinatória nada mais é do que um compilado de métodos para contar – mais precisamente, para contar possibilidades.
E, aprender a contar, é uma das coisas que primeiro nos ocorrem na vida, desde lá no período sensório-motor aos dois ou três anos de idade. Assim, é só colocar a cabeça para funcionar na hora de resolver exercícios desse tipo. Bora revisar Matemática para o Enem?
Cálculo fatorial
Para começar bem este resumo veja um resumo rápido sobre o Cálculo Fatorial, com o professor Lucas Borguezan, do canal do Curso Enem Gratuito.
Princípio Aditivo na Análise Combinatória
Suponha que um evento X possa ocorrer de x maneiras possíveis e um evento distinto Y possa ocorrer de y maneiras possíveis. Então (X ou Y) pode ocorrer de maneiras diferentes.
Exemplo: Imagine que na sua cidade tem 2 praças e 3 praias, e você só tem R$ 4,20, que é o preço da passagem para ir até um dos lugares. Caso você escolha ir à praia, terá 3 opções. Caso escolha ir à praça, terá duas opções. Logo, o número total de possibilidades dentre as quais você pode escolher uma é
2 + 3 = 5
O princípio aditivo é utilizado para contagem de eventos mais simples, mas é preciso prestar atenção no conectivo ou: você escolhe uma das praias ou você escolhe uma das praças.
Princípio Multiplicativo ou Princípio Fundamental da Contagem
Um exemplo clássico no estudo da análise combinatória é o da combinação de roupas.
Exemplo: Suponha que Júlia tenha 3 calças, uma verde, uma preta e uma azul, e 2 blusas, uma branca e uma laranja. De quantas maneiras diferentes Júlia pode se vestir?
Bem, pelo diagrama da árvore temos que:
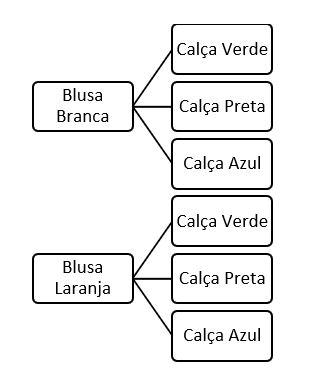
Assim, Júlia tem, no total, 6 combinações diferentes de cores de calças e blusas. Contudo, o diagrama da árvore não é o método mais eficaz para esse tipo de contagem.
Aqui, utilizamos uma pequena quantidade de dados, mas imagine se Julia tivesse 30 calças, e 55 blusas. Ia ser um trabalho e tanto para a contagem de todas as combinações, não é mesmo?
É da necessidade de contabilizar grandes quantidades e possibilidades de combinações que surge o princípio fundamental da contagem, ou também chamado de princípio multiplicativo. Ele nos diz que:
“Se uma decisão x pode ser tomada de n maneiras sucessivas e independentes e, em seguida, outra decisão y puder ser tomada de m maneiras, o número total de maneiras de tomarmos as decisões x e y será dado por n . m .”
Resumo sobre Análise Combinatória
Agora que você já dominou os fundamentos da Análise Combinatória, confira um exercício resolvido.
Exemplos de exercícios sobre análise combinatória
Vejamos através de um exemplo o que esse enunciado quer dizer na prática:
Exemplo 1: Um restaurante serve 3 pratos quentes: frango, peixe e carne; 4 tipos de saladas: salada verde, maionese, tomates e picles; e duas sobremesas: sorvete e brownie. De quantas maneiras diferentes Cláudia pode se servir, consumindo apenas um prato quente, uma sobremesa e uma salada?
Solução: veja que nesse problema temos 3 tipos diferentes de tomada de decisão
x: escolher entre frango, peixe ou carne
y: escolher entre salada verde, maionese, tomates ou picles
z: escolher entre sorvete ou brownie.
A tomada de decisão x, nos dá 3 possibilidades, a tomada de decisão y nos dá 4 possibilidades e a tomada de decisão z nos dá 2 possibilidades, sendo assim, de acordo com o enunciado temos que:
3 x 4 x 2 = 24
Cláudia tem 24 maneiras diferentes de se servir nesse restaurante.
Veja também um exemplo com possibilidades de combinações entre números naturais:
Exemplo 2: Um número de 3 algarismos distintos (centenas, dezenas, unidades) é formado por três ordens. Nesse caso, a ordem das centenas não pode levar o número zero. Vamos desenhar um esquema para melhor compreensão.
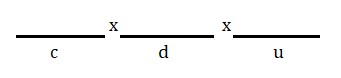
No esquema acima, temos 3 tomadas de decisão:
Escolher o algarismo das centenas diferente de zero (são 9 números do 1 ao 9, portanto, 9 opções):
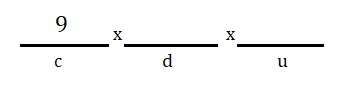
Em seguida, escolher o algarismo das dezenas diferente do que já foi escolhido para ocupar a centena (10 números do 0 ao 9, menos o que já foi escolhido, portanto, 9 opções):
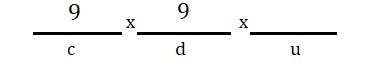
Por fim, escolher o algarismo das unidades, diferente dos que já foram utilizados para ocupar a centena e a dezena (restaram apenas 8 opções):
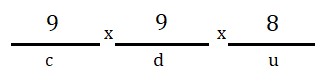
Portanto, o total de números formados por 3 algarismos é igual a 9 . 9 . 8 = 648 números.
Cálculo Fatorial
Uma ferramenta bastante utilizada em problemas de contagem é o fatorial de um número. O fatorial de um número natural nada mais é do que o produto desse número por todos os seus antecessores. O símbolo ! (exclamação) é utilizado para indicar o fatorial de um número. Veja o exemplo.
Exemplos:
5! = 5 x 4 x 3 x 2 x 1 = 120
2! = 2 x 1 = 2
O fatorial do número zero é definido por 0! = 1.
Pode-se utilizar simplificações para trabalhar com fatorial, como:
Exemplo:
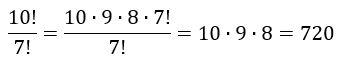
O uso do fatorial na análise combinatória facilita muito alguns cálculos. Guarde essas informações para os estudos posteriores de tipos de ferramentas utilizadas na análise combinatória.
Videoaula
Para mais estudar mais sobre análise combinatória, veja o vídeo do canal do Curso Enem Gratuito e, em seguida, resolva os exercícios:
Exercícios sobre análise combinatória
-
1. Pergunta
(FAMERP SP/2018)
Lucas possui 6 livros diferentes e Milton possui 8 revistas diferentes. Os dois pretendem fazer uma troca de 3 livros por 3 revistas. O total de possibilidades distintas para que essa troca possa ser feita é igual a
-
2. Pergunta
(UCB DF/2019)
A equipe plantonista do centro cirúrgico de um hospital é composta de 1 médico anestesista, 2 médicos cirurgiões, 1 instrumentista cirúrgico, 1 enfermeiro, 1 técnico de enfermagem e 1 auxiliar de enfermagem. Concorrem a essa escala 3 médicos anestesistas, 7 médicos cirurgiões, 4 instrumentistas cirúrgicos, 5 enfermeiros, 4 técnicos de enfermagem e 6 auxiliares de enfermagem. De quantas formas distintas a equipe de plantão do centro cirúrgico desse hospital pode ser formada?
-
3. Pergunta
(UNIDERP MS/2018)
Em uma clínica hospitalar, trabalham, em regime especial de plantão, 8 médicos e 5 enfermeiros.
Para se constituir uma junta médica especial composta de 4 médicos e 2 enfermeiros, existem n maneiras distintas e o valor de n é -
4. Pergunta
(UNEB BA/2018)
Um grupo de 8 enfermeiros contratados por um hospital deve ser distribuídos de modo que 3 fiquem no setor de pronto-socorro, 3 no setor cirúrgico e os demais na ala pediátrica. O número de maneiras distintas de se fazer tal distribuição é igual a
-
5. Pergunta
(UCB DF/2018)
Na loteria federal, serão sorteados 6 números. João comprou um bilhete com 6 palpites, e José, um bilhete com 8 palpites. A razão entre as chances de José e João, respectivamente, acertarem os 6 números é
-
6. Pergunta
(UEFS BA/2018)
Em uma festa, estão presentes 13 homens e 16 mulheres. Três passagens aéreas serão sorteadas para 3 dessas pessoas. O número de maneiras distintas como essas passagens podem ser sorteadas, de modo que pelo menos um homem e pelo menos uma mulher sejam contemplados, é
-
7. Pergunta
(FPS PE/2018)
Para a realização de certa cirurgia são necessários 2 cirurgiões, 1 anestesista e 3 enfermeiros. Dentre os profissionais de um hospital aptos para realizar a cirurgia, estão 5 cirurgiões, 4 anestesistas e 10 enfermeiros. De quantas maneiras pode ser constituída a equipe que fará a cirurgia?
-
8. Pergunta
(UNICESUMAR PR/2018)
Um time de voleibol é composto por 14 jogadores, tal que 6 jogadores são considerados principais, 5 jogadores são considerados reservas e 3 jogadores são considerados líberos. Para participar de um campeonato de Voleibol, não importando a posição que cada jogador ocupa em quadra, o técnico deve formar sua equipe com 9 jogadores, sendo 4 deles escolhidos entre os titulares, 4 escolhidos entre os reservas e 1 escolhido entre os líberos. De quantas maneiras diferentes esse técnico pode formar a equipe que irá participar desse campeonato?
-
9. Pergunta
(UNITAU SP/2018)
Para realizar um estudo das propriedades químicas e de seus respectivos efeitos quando associados, um médico tem 10 tipos de medicamentos disponíveis em um laboratório de farmacologia. O número de maneiras possíveis para associar 6 desses medicamentos, com quantidades iguais, sabendo que, dentre eles, 2 não podem estar na mesma mistura por causarem reações medicamentosas negativas, é
-
10. Pergunta
(PUC SP/2018)
A secretária de um médico precisa agendar quatro pacientes, A, B, C e D, para um mesmo dia. Os pacientes A e B não podem ser agendados no período da manhã e o paciente C não pode ser agendado no período da tarde. Sabendo que para esse dia estão disponíveis 3 horários no período da manhã e 4 no período da tarde, o número de maneiras distintas da secretária agendar esses pacientes é
