O Princípio Fundamental da Contagem diz que o número total de possibilidades é o produto dos números de possibilidades em cada etapa. Veja agora no resumo com dicas e exercícios:
Probabilidade é um tema bastante recorrente no Enem. Nos últimos anos, mais de quarenta questões envolveram este tema, sempre relacionando a probabilidade com temas cotidianos. Portanto, aprender contagem e estatística é fundamental para alcançar uma boa nota!
Princípio Fundamental da Contagem (PFC)
O Princípio Fundamental da Contagem diz que o número total de possibilidades é o produto dos números de possibilidades em cada etapa. O Princípio Fundamental da Contagem também é chamado de Princípio Multiplicativo.
Exemplos de contagem
Para entender melhor, vamos ver um exemplo:
- Quantos anagramas podemos escrever com as letras da palavra amor?
Lembre-se: anagrama é uma “palavra” formada pela transposição (troca ou “embaralhamento”) das letras de outra palavra.
Para escrever vários anagramas com as letras da palavra amor, temos as seguintes possibilidades:
- Número de possibilidades de escolher a primeira letra = 4
- Número de possibilidades de escolher a segunda letra = 3
- Número de possibilidades de escolher a terceira letra = 2
- Número de possibilidades de escolher a última letra = 1
Então o número de anagramas será o produto das possibilidades:
n = 4.3.2.1 = 24 anagramas possíveis
O Princípio fundamental da Contagem:
Aprenda agora com o professor Lucas Borguesan, do canal do Curso Enem Gratuito.
Entendeu? Vejamos outro exemplo:
Com os algarismos 0, 1, 2, 3, 4, 5, 6 e 7:
- Quantos números de 3 algarismos podemos formar?
____________ __________ __________
Centena Dezena Unidade
Então, temos 7 possibilidades para a centena (0 não é permitido), 8 para a dezena e 8 para a unidade (pois os números podem se repetir).
Portanto, podemos formar: 7. 8. 8 = 448 números.
- Fácil, não é mesmo? Podemos dificultar um pouco? Qual a quantidade de números de 3 algarismos distintos que conseguimos formar?
Atenção: Agora não poderemos repetir os números na centena, dezena e na unidade, portanto teremos: 7 possibilidades para a centena (não podemos contar com o 0), 7 para a dezena (pois aqui teremos a inclusão do número zero, excluído na casa da centena) e 6 para a unidade. Assim, podemos formar 7. 7 . 6 = 294 números de 3 algarismos distintos com os algarismos 0, 1, 2, 3, 4, 5, 6 e 7.
Probabilidade
Uma das principais aplicações das técnicas de contagem é a resolução de problemas simples de probabilidade. O interesse dos matemáticos no estudo sistemático de probabilidades é relativamente recente e tem suas raízes no estudo dos jogos de azar.
Aprenda a resolver Probabilidade
Confira agora com o professor Lucas Borguesan, do canal do Curso Enem Gratuito.
No estudo desses jogos, normalmente ocorre a seguinte situação: todos os possíveis resultados têm a mesma chance de ocorrer.
Por exemplo, ao lançar um dado “honesto” (quer dizer, construído de forma perfeitamente cúbica e homogênea), todas as faces têm a mesma chance de sair. Como as faces são 6, esperamos que cada uma delas ocorra em aproximadamente 1/6 dos lançamentos.
Dizemos, então, que cada uma delas tem probabilidade 1/6 de sair. Também atribuímos probabilidades a conjuntos de resultados possíveis, chamados de eventos.
Achou complicado? Vamos ver um exemplo para ficar mais claro:
- Qual é a probabilidade de se obter um resultado maior que 4 ao se lançar um dado honesto?
Quando falamos em sair um número maior do que 4 ao jogar o dado, estamos considerando sair o número 5 ou 6, como cada face do dado tem a probabilidade de 1/6 de ocorrer, a probabilidade de sair um número maior que 4 será :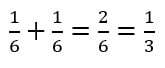 
Tipos de combinatória
O princípio fundamental da contagem pode ser usado em grande parte dos problemas relacionados com contagem. Entretanto, em algumas situações seu uso torna a resolução muito trabalhosa. Desta maneira, existem algumas técnicas para resolver problemas com determinadas características. As mais comuns são: arranjos, combinações e permutações.
No entanto, nos problemas que utilizam essas técnicas, é comum aparecerem multiplicações envolvendo números naturais consecutivos, como, por exemplo: 26. 25. 24 ; 4 . 3 . 2 . 1 ; 7 . 6 . 5; etc., portanto, precisamos relembrar uma ferramenta muito utilizada para resolver os problemas de contagem, que é o fatorial.
Usando fatorial para resolver um problema de contagem
Fatorial: Seja n um número natural, com n ≥ dois. Define-se o fatorial de n, que é representado por n!, como o produto dos números naturais consecutivos n, n – 1, n – 2, …, 1. Isto é: n! = n . (n – 1). (n – 2). … . 1
Importante: 0! = 1 e 1! = 1
Vamos ver alguns exemplos:
Arranjos
Consideramos arranjo, quando a ordem dos elementos for levada em consideração, ou seja, os agrupamentos forem diferentes entre si pela ordem dos elementos.
Para calcular a quantidade de agrupamentos formados utilizamos seguinte fórmula:
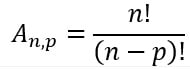
n é a quantidade de elementos do conjunto.
p é um número natural menor ou igual a n, que representa a união dos elementos na formação dos agrupamentos.
Exemplo:
Em um colégio, dez alunos candidataram-se para ocupar os cargos de presidente e vice-presidente do grêmio estudantil. De quantas maneiras distintas a escolha poderá ser feita?
Resolução:
Temos dez alunos disputando duas vagas, onde a ordem de escolha mudará o agrupamento, então se trata de um problema de arranjo, assim, dez elementos tomados dois a dois, temos:
P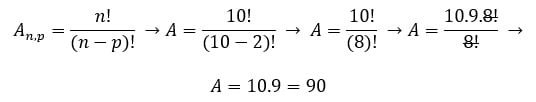
Permutação
São agrupamentos ordenados, onde o número de elementos (n) do agrupamento é igual ao número de elementos disponíveis. Observe que a permutação é um caso especial de arranjo, quando o número de elementos é igual ao número de agrupamentos. Desta maneira, o denominador na fórmula do arranjo é igual a 1 na permutação.
Exemplo:
Em uma mesa existem 6 lugares, quantas maneiras diferentes 6 pessoas podem sentar-se nessas mesas?
Resolução:
Como a ordem em que irão se sentar é importante e o número de lugares é igual ao número de pessoas, iremos usar a permutação:
Combinação
Na combinação simples, a ordem dos elementos no agrupamento não interfere. São arranjos que se diferenciam somente pela natureza de seus elementos. É dada pela seguinte expressão: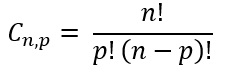
Um exemplo clássico de combinação é a mega sena, que consiste em uma cartela de 60 números dentre os quais devemos acertar 6 (prêmio principal), portanto temos uma combinação onde n = 60 e p = 6, sessenta números tomados seis a seis.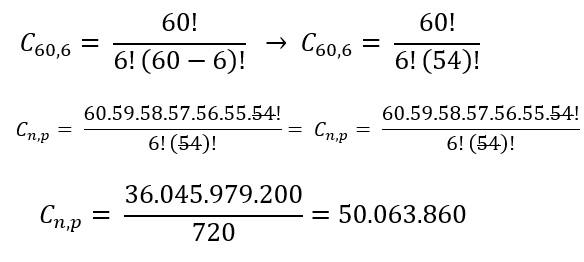 
Continue aprendendo com o prof. Sérgio, que preparou uma videoaula especial para nosso canal!
Exercícios sobre contagem e probabilidade
Para terminar, resolva os exercícios sobre contagem e probabilidade selecionados!
.
