Aprenda a fazer contas que valem pontos preciosos na Matemática. O Cálculo de Porcentagem vale para achar o lucro, descontos e aumentos. Veja resumo com aula grátis:
Sabe quando você vai fazer aquela comprinha esperta e sempre chora por um desconto para o vendedor? Geralmente, as lojas oferecem um desconto para produtos pagos à vista, e um aumento caso você resolva pagar em prestações. Esta conta embute um cálculo de porcentagem.
Esse é um exemplo bacana de como os aumentos e descontos percentuais estão presentes no seu dia a dia. Portanto, este não é apenas um assunto que cai no Enem – embora ele seja muito cobrado! Saber como calcular porcentagem é bem importante também para você que quer sempre lucrar na hora de fazer aquela compra.
Como calcular porcentagem
Você pode nunca ter ouvido falar em matemática financeira, mas com certeza já lidou com dinheiro, já comprou uma roupa e já ouviu falar em lucro. Quando falamos em lucro estamos falando de um “bônus”. Se uma pessoa lucrou em um investimento, significa que ela saiu dele com mais dinheiro do que entrou.
O lucro (L) é relacionado diretamente com o preço de compra, o qual determinaremos aqui por C, e com o preço de venda, determinado por V. O cálculo do lucro é bastante simples, basta subtrair o valor de compra (C) do valor de venda (V), podendo utilizar a fórmula
L = V – C
Resumo sobre o cálculo de porcentagem
Aprenda a calcular porcentagem na prática com o resumo em vídeo do professor Lucas!
Exemplos de cálculo de porcentagem
Para entender melhor como calcular porcentagem, vamos apresentar alguns exemplos.
Exemplo 1
Carlos comprou um quadro ligeiramente danificado por 75 reais. Carlos restaurou o quadro e vendou para um amigo por 110 reais. Qual foi o lucro de Carlos?
Para calcular o lucro, nesse caso, vamos primeiro determinar os valores de compra e venda
C = 75 reais
V = 110 reais
Lucro: L = V – C
L = 110 – 75 = 35
Exemplo 2
Julia faz bolo para vender na faculdade. Ela gasta em média 60 reais para comprar os ingredientes para fazer um bolo de 15 pedaços. Julia vende cada pedaço por 3,50 reais. Qual o lucro de Julia com a venda dos bolos?
Primeiramente vamos calcular quanto ela ganha vendendo os 15 pedaços por 3,50.
15 x 3,50 = 52,50
Então, o preço de venda é 52,50, e o preço de compra é de 60 reais.
Calculando o lucro:
L = V – C
L = 52,50 – 60
L = – 7,5
Julia está tendo lucro com a venda de seus bolos? Não!
O “lucro negativo” indica prejuízo. Logo, para se obter lucro o valor de venda sempre precisa ser maior do que o valor de compra!
Aumentos e descontos percentuais
Para compreender o cálculo e a fórmula de aumentos e descontos percentuais, vamos utilizar exemplos. Comecemos com o aumento:
Exemplo do cálculo de aumento percentual
Você queria comprar uma televisão em 2017 e ela custava 1000 reais, mas você não tinha o dinheiro. Agora você tem o dinheiro, mas o preço da televisão aumentou 30%. Quanto está custando a televisão?
Para fazer esse cálculo devemos seguir alguns passos. Primeiro, você sabe que o valor sofreu um aumento de 30%, então vamos calcular esse valor.
Lembre-se que 30% é igual a , que equivale a 0,3. Então, 30% de 1000 reais é calculado como:
30% de 1000 = 0,3 x 1000 = 300
300 reais é o tanto que o valor aumentou, então, o valor atual da televisão é de
1000 + 300 = 1.300 reais.
Essas questões sobre aumentos percentuais costumam confundir bastante o aluno em provas de vestibular, porque geralmente são mais complexas do que a do exemplo citado. Aí é bem fácil de confundir os valores e esquecer de somar o valor do aumento com o valor inicial. Para resolver isso, existe uma fórmula bastante conhecida no estudo das porcentagens que eu vou te explicar a seguir.
Usando o final do exemplo anterior como base, temos a equação abaixo:
1000 + 300 = 1300
Mas, o que representa o valor 300? Representa o cálculo dos 30% sobre o produto. Então podemos reescrever a equação como:
1000 + (0,3 x 1000) = 1300
Além disso, podemos isolar o valor inicial 1000, simplificando a equação:
1000 + (1 + 0,3) = 1300
Na equação acima temos que 1000 é o valor inicial (VI), 0,3 é a taxa percentual decimal (TD), e 1300 é o valor final (VF), resultando na seguinte fórmula:
V1 (1 + TD) = VF
Que pode ser reescrita para facilitar o entendimento, ficando:
VF = (1 + TD) VI
Exemplo do cálculo do desconto percentual
Já para o cálculo do desconto percentual, o cálculo é bem parecido, somente alterando o sinal de soma para o sinal de subtração.
Assim, a fórmula acima fica desse jeito:
VF = (1 – TD) VI
Vamos ver como se aplica em um exemplo?
Luiza fez uma compra no supermercado e o valor foi R$ 82,00. O desconto para pagamento à vista e no dinheiro é de 15%. Qual o valor final da compra dentro dessa condição?
Se o desconto é de 15% significa que a taxa percentual decimal será de 0,15, logo, podemos aplicar na fórmula os valores.
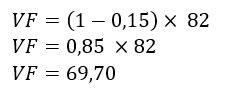
O valor final da compra foi de 69,70 reais.
Exercícios sobre o cálculo porcentagem
Para terminar, resolva os exercícios sobre o cálculo de porcentagem a seguir!
Questão 01)
Um torcedor de um time de futebol do estado do Ceará comprou uma camisa do seu time por 80 reais. Uma semana depois, a loja aumentou seus preços em 30%, mas como as vendas não estavam correspondendo, resolveu fazer uma liquidação, colocando um desconto de 30% em todos os seus produtos. Se o mesmo torcedor voltasse a mesma loja depois desse aumento e do sucessivo desconto compraria a mesma camisa por:
- a) 70 reais.
- b) 71,50 reais.
- c) 72 reais.
- d) 72,80 reais.
- e) 73 reais.
Gab: D
Questão 02)
Para aumentar as vendas no início do ano, uma loja de departamentos remarcou os preços de seus produtos 20% abaixo do preço original. Quando chegam ao caixa, os clientes que possuem o cartão fidelidade da loja têm direito a um desconto adicional de 10% sobre o valor total de suas compras.
Um cliente deseja comprar um produto que custava R$ 50,00 antes da remarcação de preços. Ele não possui o cartão fidelidade da loja.
Caso esse cliente possuísse o cartão fidelidade da loja, a economia adicional que obteria ao efetuar a compra, em reais, seria de
- a) 15,00.
- b) 14,00.
- c) 10,00.
- d) 5,00.
- e) 4,00.
Gab: E


