Como calcular porcentagem
Vem com a gente estudar como calcular juros e porcentagem para arrebentar nas questões de Matemática no Enem! Depois da aula tem uma lista de exercícios pra você treinar!
Você sabia que em todas as provas do Enem têm questões com o tema porcentagem? Você sabe como usá-las para a resolução de problemas? Vem com a gente aprender e arrebentar na prova do Enem!
Fazendo uma análise de todas as provas de Matemática do Enem podemos perceber um padrão: sempre encontramos questões envolvendo estimativas, descontos, juros, acréscimo, taxas, problemas envolvendo geometria e estatística.
Juros e porcentagem
Todas estas questões estão entre as que mais cai no Enem. E, além disso, elas têm uma coisa em comum: a porcentagem, que nada mais é do que uma aplicação de números decimais.
Logo, você precisa dominar muito bem esse tema para aplicar em outras áreas da matemática e gabaritar suas questões do Enem.
O termo porcentagem vem do latim per centum, que quer dizer “por cento” ou a cada centena. Por isso em Matemática dizemos que a porcentagem é a razão entre uma grandeza e sua centésima parte.
Ouvimos e lidamos com as porcentagens praticamente a vida toda, como quando adquirimos um desconto, pagamos juros de contas em atraso ou em empréstimos, quando pagamos taxas, quando ouvimos falar em alíquotas ou percentuais. Imagem: Freepick.com. <https://goo.gl/fVE8rZ>.
Imagem: Freepick.com. <https://goo.gl/fVE8rZ>.
Nas provas do Enem, a contextualização dos problemas se dá envolvendo situações de economia, tratamento de informações como número de habitantes por metro quadrado, em geometria – onde um lado de uma figura pode ser comparado com outro através de taxa percentual –, etc.
Vamos entender como podemos calcular a porcentagem e depois vamos analisar algumas situações que aparecem nas provas do Enem.
Representação da porcentagem ou percentual
Uma taxa de juros, acréscimo ou desconto é dada através de um número inteiro ou decimal seguido do sinal de porcentagem %, como 10% (dez por cento), 0,35% (zero vírgula trinta e cinco porcento), 2,75% (dois vírgula setenta e cinco por cento), entre outros.
Como calcular a porcentagem
Para que fique mais fácil de compreender a aplicação da porcentagem, vamos partir de alguns exemplos. Vale a pena esclarecer que temos várias formas de calcular a porcentagem, neste post usaremos a forma mais tradicional. Vamos ao primeiro exemplo:
Uma propaganda na TV mostra que uma loja de uma grande rede de eletrodomésticos está dando 30% de desconto em uma compra à vista. O que isso quer dizer?
Se loja está dando desconto, vamos pagar um valor menor e temos que ter certeza que não estamos sendo enganados. Logo, temos que calcular o preço antes do vendedor, não é mesmo?
Como fazer isso? Digamos que você queira comprar uma SmartTV que tem o preço real igual a R$ 1899,00. Para calcularmos os 30% de desconto precisamos multiplicar o valor do produto por 30. E depois dividir por 100:
1899,00 X 30 = 56 970,00
56 970,00 : 100 = 569,70
Agora calculamos o valor a ser pago temos que diminui o desconto do valor total do produto:
1899,00 – 569,70 = 1 329, 30.
Resultado: Como você pode ver, com o desconto da promoção, a TV sai por R$ 1 329,30.
Mas lembre-se de ter certeza que a empresa está dando o desconto sobre o preço real do produto, ok?
Resumo sobre como calcular de porcentagem
Como calcular juros
Gostou do exemplo? Vamos mostrar mais um. Agora, com taxa de juros:
A prestação de meu notebook é de R$ 735,40 e no boleto diz que após a data de vencimento tem um acréscimo de 3,5% ao dia. Se eu atrasasse o pagamento desse boleto em um dia, quanto pagaria no total?
Para calcular um acréscimo, temos que primeiro descobrir em reais quanto será essa taxa e para isso temos que multiplicar o valor do boleto pela taxa dada:
735,40 X 3,5 = 2 573,9
Depois dividimos o resultado por 100:
2 573,9 : 100 = 25,739
Agora, somamos esse valor ao valor do boleto:
735, 40 + 25, 739 = 761,139
Perceba que a taxa que calculamos foi para um dia de atraso e foi bem salgada, se atrasarmos mais dias temos que multiplicar essa taxa pelos dias de atraso e depois somar ao valor do boleto.
Pagar juros e taxas não é legal! Por isso, temos que nos organizar para não pagarmos muito mais que o valor justo pelo produto ou serviço.
Números decimais e porcentagem
Como já lembramos temos outras formas de calcular e aplicar as porcentagens, uma outra forma é transforma a taxa em um número decimal. Observe o exemplo acima resolvido nessa forma diferente:
A taxa é 3,5% = 3,5/100 = 0,035
Depois multiplicamos o valor do boleto:
735,40 X 0, 035 = 25, 739
E somamos no final:
735, 40 + 25, 739 = 761,139
Agora que você concluiu a revisão completa, é hora de testar seus conhecimentos. Vem!
Exercícios sobre porcentagem
Para terminar, resolva os exercícios sobre porcentagem selecionados pela equipe do Curso Enem Gratuito!
Sumário do Quiz
0 de 10 questões completadas
Perguntas:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
Information
.
Você já fez este questionário anteriormente. Portanto, não pode fazê-lo novamente.
Quiz is loading...
You must sign in or sign up to start the quiz.
Para iniciar este questionário, você precisa terminar, antes, este questionário:
Resultados
0 de 10 perguntas respondidas corretamente
Seu tempo:
Acabou o tempo
Você conseguiu 0 de 0 pontos possíveis (0)
| Pontuação média |
|
| Sua pontuação |
|
Categorias
- Sem categoria 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- Respondido
- Revisão
-
Pergunta 1 de 10
1. Pergunta
(UNEMAT MT/2016)
Nas lojas de móveis geralmente encontramos um vendedor com uma calculadora simples em mãos. Nas vendas esse vendedor rapidamente calcula o desconto. Suponhamos que na compra de um determinado guarda-roupas é oferecido um desconto de 5%. Hoje a calculadora está com defeito e ele fará a conta à mão.
Para mostrar ao cliente o preço do guarda-roupas já com desconto, basta efetuar a seguinte multiplicação:
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre porcentagem para acertar na hora da prova!
-
Pergunta 2 de 10
2. Pergunta
(UNIFOR CE/2018)
Uma loja resolveu fazer uma promoção de um determinado brinquedo no Dia das Crianças. A promoção era a seguinte: “Compre x brinquedos e ganhe x% de desconto”. A promoção é válida para compras até 60 brinquedos, caso em que é concedido o desconto máximo de 60%. Edno, Erivando, Francisco, Paulo e Ricardo compraram 10, 15, 20, 30 e 45 unidades do brinquedo que estava em promoção, respectivamente.

Qual deles poderia ter comprado mais brinquedos e gasto a mesma quantia, se empregasse melhor seus conhecimentos de Matemática?
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre porcentagem para acertar na hora da prova!
-
Pergunta 3 de 10
3. Pergunta
(UNCISAL/2018)
Um biólogo está estudando o crescimento de um animal. Quando ele inicia sua pesquisa, o animal pesa 50 kg. No período de 1 mês, o peso desse animal aumenta em 20% e, no segundo mês, o peso aumenta novamente em 20%. Nessas condições, o aumento do peso desse animal, considerando os dois meses, foi de
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre porcentagem para acertar na hora da prova!
-
Pergunta 4 de 10
4. Pergunta
(PUCCampinas SP/2018)
Lembrando e pensando a TV
1 Houve um tempo em que a TV − acreditem, ó jovens! 2 − ainda não existia. Ouvia-se rádio, ia-se ao cinema. 3 Mas um dia chegou às casas das pessoas um aparelho 4 com o som vivo do rádio acoplado a vivas imagens, 5 diferentes das do cinema, imagens chegadas de 6 algum lugar do presente, “ao vivo”. Logo saberíamos 7 que todas as imagens do mundo, inclusive os filmes do 8 cinema, poderiam estar ao nosso alcance, naquela 9 telinha da sala. Modificaram-se os hábitos das famílias, 10 seus horários, sua disponibilidade, seus valores. A TV 11 chegou para reinar.
12 A variedade da programação já indicava o amplo 13 alcance do novo veículo: notícias, reportagens, musicais, 14 desenhos animados, filmes, propagandas, seriados, 15 esportes, programas humorísticos, peças de teatro 16 − tudo desfilava ali, diante dos nossos olhos, ainda no 17 tubo comandado por grandes válvulas e com imagem 18 em preto e branco. Boa parte dos primeiros aparelhos 19 de TV tinham telas de 16 a 21 polegadas, acondicionadas 20 numa enorme e pesada caixa de madeira. Havia 21 uns três ou quatro canais, com alcance bastante limitado 22 e programação restrita a cinco ou seis horas por dia. 23 Mais tarde as transmissões passariam a ser via satélite 24 e ocupariam as 24 horas do dia.
25 Os custos da programação eram pagos pela publicidade, 26 que tomava boa parte do tempo de transmissão. 27 Vendia-se de tudo, de automóveis a margarina, de xaropes 28 para tosse a apartamentos. Filmetes gravados e 29 propagandas ao vivo sucediam-se e misturavam-se a 30 notícias sobre exploração espacial, enquanto documentários 31 estrangeiros falavam da revolução russa, da 32 II Guerra, do nazismo e do fascismo, das convicções 33 pacifistas de Ghandi, das ideias do físico Einstein sobre 34 a criação e a legitimação da ONU etc. etc. Já as incursões 35 históricas propiciadas pelos filmes nos levavam ao 36 tempo de Moisés e do Egito Antigo, ao Império Romano 37 e advento do Cristianismo, tudo entremeando-se ao 38 humor de Chaplin, às caretas de Jerry Lewis e às trapalhadas 39 das primeiras comédias nacionais do gênero 40 chanchada. Houve também o tempo em que as famílias 41 se agrupariam diante dos festivais da canção, torcendo 42 por músicas de protesto, baladas românticas ou de 43 ritmos populares “de raiz”. Enfim, a TV oferecia a um público 44 extasiado um espetáculo variadíssimo, tudo nas 45 poucas polegadas do aparelho, que não tardou a incorporar 46 outras medidas, outros sistemas de funcionamento, 47 projeção em cores e controle remoto.
48 As telas de plasma, o processo digital e a interface 49 com a informática foram dotando a TV de muitos outros 50 recursos, até que, bem mais tarde, tivesse que enfrentar 51 a concorrência de outras telas, muito menores, portáteis, 52 disponíveis nos celulares, carregados de aplicativos e 53 serviços. Apesar disso, nada indica que a curto prazo 54 desapareçam da casa os aparelhos de TV, enriquecidos 55 agora por incontáveis dispositivos.
56 No plano da cultura e da educação, a televisão 57 teve e tem papel importante. Os telecursos propiciam 58 informação escolar específica nas áreas de Matemática, 59 Física, História, Química, Língua e Literatura, fazendo 60 as vezes da educação formal por meio de incontáveis 61 dispositivos pedagógicos, inclusive a dramatização de 62 conteúdos. Aqui e ali há entrevistas com artistas, políticos, 63 pensadores e personalidades várias, atualizando 64 ideias e promovendo seu debate. No campo da política, 65 é relevante, às vezes decisivo, o papel que a TV tem na 66 formação da opinião pública. A ecologia conta, também, 67 com razoável cobertura, informando, por exemplo, sobre 68 os benefícios da reciclagem de lixo, da cultura de produtos 69 orgânicos e da energia solar.
70 Seja como forma de entretenimento, veículo de 71 informação, indução aos debates e repercussão atualizada 72 dos grandes temas de interesse social, a TV vem 73 garantindo seu espaço junto a bilhões de pessoas no 74 mundo todo. Por meio dela, acompanhamos ao vivo momentos 75 agudos da política internacional, a divulgação 76 de um novo plano econômico do governo, a escalada da 77 violência urbana. Ao toque de uma tecla do controle remoto, 78 você pode se transferir, aleatoriamente, do palco 79 de um ataque terrorista para o final meloso de uma comédia 80 romântica.
81 Numa espécie de espelhamento multiplicativo e 82 fragmentário da nossa vida e dos poderes da nossa 83 imaginação, a TV vem acompanhando os passos da 84 vida moderna e ditando, mesmo, alguns deles, sem dar 85 sinal de que deixará tão cedo de nos fazer companhia.
(Percival de Lima e Souto, inédito)
Segundo dados do IBGE, em 2014 a TV estava presente em 97,1% dos 67 milhões de domicílios brasileiros. De acordo com esse dado, a quantidade de domicílios brasileiros sem TV em 2014 era igual a
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre porcentagem para acertar na hora da prova!
-
Pergunta 5 de 10
5. Pergunta
(ESPM SP/2018)
Por volta de 2010, a distribuição da população indígena por região do Brasil era representada pelo gráfico abaixo:
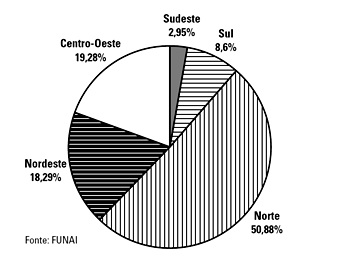
Considerando-se que a população indígena total estimada para aquela época era de 325 200, podemos concluir que, na região Sul, o número de indígenas era de aproximadamente:
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre porcentagem para acertar na hora da prova!
-
Pergunta 6 de 10
6. Pergunta
(UNIFOR CE/2018)
Paraná, o maior produtor de trigo do Brasil em 2016, será representado no gráfico abaixo pelo Estado A, enquanto Mato Grosso, o maior produtor de soja de 2016, será representado pelo Estado B. Como podemos observar, os gráficos abaixo representam a produção relativa de grãos de cada um desses estados.
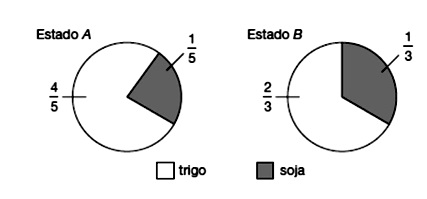
Sendo assim, a produção de trigo do estado do Paraná corresponde a que porcentagem da produção de grãos desse estado?
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre porcentagem para acertar na hora da prova!
-
Pergunta 7 de 10
7. Pergunta
(FATEC SP/2018)
Os salários de um homem branco, uma mulher e um homem negro foram somados, resultando em R$ 4.380,00. Sabe-se que o salário dessa mulher é igual a 62% do salário desse homem branco, e o salário desse homem negro é igual a 57% do salário desse homem branco.
Com base nessas informações, o salário dessa mulher e desse homem negro são, respectivamente, iguais a
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre porcentagem para acertar na hora da prova!
-
Pergunta 8 de 10
8. Pergunta
(UNESP SP/2018)
Os estudantes 1, 2 e 3 concorreram a um mesmo cargo da diretoria do grêmio de uma faculdade da UNESP, sendo que 1 obteve 6,25% do total de votos que os três receberam para esse cargo. Na figura, a área de cada um dos três retângulos representa a porcentagem de votos obtidos pelo candidato correspondente. Juntos, os retângulos compõem um quadrado, cuja área representa o total dos votos recebidos pelos três candidatos.
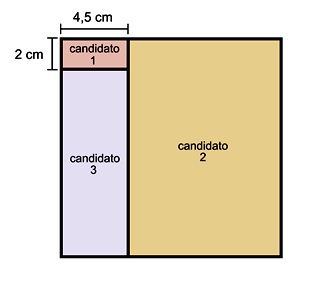
Do total de votos recebidos pelos três candidatos, o candidato 2 obteve
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre porcentagem para acertar na hora da prova!
-
Pergunta 9 de 10
9. Pergunta
(UERJ/2018)
No mapa mensal de um hospital, foi registrado o total de 800 cirurgias ortopédicas, sendo 440 em homens, conforme os gráficos abaixo.
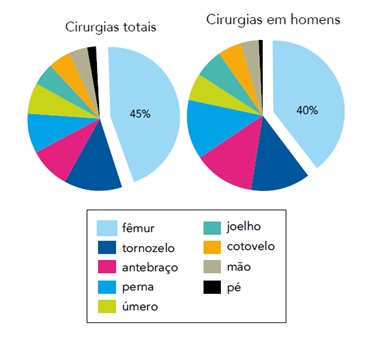
De acordo com esses dados, o número total de cirurgias de fêmur realizadas em mulheres foi:
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre porcentagem para acertar na hora da prova!
-
Pergunta 10 de 10
10. Pergunta
(UFPR/2018)
Em julho deste ano, os brasileiros foram surpreendidos com uma alteração da alíquota do PIS e Cofins que resultou em um aumento de R$ 0,41 por litro de gasolina, elevando seu preço médio para R$ 3,51. De quanto foi o aumento percentual aproximado do preço médio da gasolina causado por essa alteração de alíquota?
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre porcentagem para acertar na hora da prova!
Sobre o(a) autor(a):
Suelen Rocha -
Gostou? Compartilhe!
Continue lendo:
Aqui vão 2 publicações relacionadas que talvez você goste:

Como resolver a prova de Matemática no Enem 2024? Veja as dicas do professor
Por Melina Zanotto | 08 de novembro
Confira as orientações e estratégias do professor Lucas Borguezan para se sair bem na prova de Matemática no Enem 2024.

Aulão Enem de Matemática: revisão intensiva e gratuita para a prova
Por João Vianney dos Valles Santos | 11 de outubro
Assista ao Aulão Enem de Matemática do Curso Enem Gratuito e revise os conteúdos mais importantes para a prova.


