Dízimas periódicas e não periódicas: simples e compostas
Você sabe o que são dízimas? E como fazemos os cálculos com elas? Vem com a gente aprender sobre o tema dízimas periódicas e dízimas não periódica no Curso Enem Gratuito.
Nesta aula, você vai entender que os números decimais podem se apresentar como dízimas. Além disso, compreenderá a diferença entre a dízima finita e a infinita e vai diferenciar as dízimas que fazem parte de conjuntos numéricos diferentes.
Essas dízimas podem ser denominadas de periódicas ou não periódicas. E, é claro, aprenderá como transformar Dízimas Periódicas Simples e Compostas em sua fração geratriz.
Vem com a gente revisar esses conceitos de Matemática Básica para não dar bobeira no Enem e nos Vestibulares!
O que é uma dízima?
A palavra dízima vem do latim e significa “décima”. Na matemática, dízimas são números decimais. As dízimas podem ser:
- Finitas: são números racionais que tem um fim. Exemplo: 2,46.
- Infinitas: podem ser números racionais ou irracionais. Exemplo: 0,464646…
As dízimas infinitas podem ser classificadas como periódicas ou não periódicas:
a) Dizimas periódicas: são números decimais que pertencem ao conjunto dos números racionais.
Lembre-se de que número racional é todo o número que pode ser representado por uma razão (ou fração) entre dois números inteiros (com denominador diferente de zero), podendo apresentar ainda a forma decimal (casos em que não há resto).
b) Dízimas não periódicas pertencem ao conjunto dos números irracionais.
Números irracionais são números decimais infinitos e não periódicos, o que podemos concluir que não há um período. Por exemplo, o número Pi:![]()
Dica do Curso Enem Gratuito: Quer aprofundar seus estudos? Indico esta aula do Blog do Enem sobre Transformação de Números Decimais para Frações.
Resumo para entender as dízimas
Confira agora com o professor Lucas Borghesan, do canal do Youtube do Curso Enem Gratuito as principais dicas sobre as Dízimas Periódicas.
A base para você dominar as dízimas periódicas começa com a transformação dos números decimais em frações, e vice-versa. Confira com o professor Lucas aí acima.
Entendendo as dízimas periódicas
Outra coisa importante que precisamos lembrar sobre as dízimas periódicas é que elas são números formados por infinitos algarismos que se repetem periodicamente. E o número que se repete é chamado de período.
As dízimas periódicas são classificadas em simples ou compostas.
Observe os exemplos de dízimas periódicas simples:
a) 1, 44444 – O período da dízima é 4.
b) 0,565656 – O período é 56.
Note que para reconhecermos o período, basta olharmos para o número que se encontra logo após a vírgula.
As Dízimas Compostas têm entre o período e a vírgula, uma parte não-periódica.
Veja os exemplos a seguir:
a) 3,422222 – Note que após a vírgula temos o número 4 e, em seguida, o número 2 se repete várias vezes. Sendo assim, neste exemplo, o período é 2 e a parte não-periódica é 4.
b) 0, 256666 – Neste outro exemplo, o período é 6 e a parte não-periódica é 25.
Geratriz de uma dízima periódica
A geratriz é uma fração que originou a dízima periódica. Veja como encontrar a fração geratriz dos diferentes tipos de dízimas periódicas:
- Fração geratriz de uma dízima periódica simples:
Para encontrar a fração geratriz de uma dízima periódica simples, basta escrever a fração com numerador igual ao período e o denominador 9.
Exemplo: Transforme a Dízima Periódica Simples em uma fração Geratriz:
a) 0, 22222… =
O período da Dízima Periódica Simples é 2 então a fração geratriz é 2/9.
b) 0,151515151515…=
O período da Dízima Periódica Simples é 5, logo a fração Geratriz é 15/99.
Veja que o número de “números 9” no denominador é igual ao número de algarismos do período.
- Fração geratriz de uma dízima periódica simples com período não-inteiro:
Quando a dízima apresentar um período não-inteiro, devemos separá-la em duas partes: inteira e decimal, somadas. Depois, transformamos a parte decimal em fração Geratriz de uma Dízima Periódica Simples e aplicamos a soma de fração para encontrar a solução final:
Exemplo: 1,4545 =
a) separamos em duas partes: inteira e decimal, somadas:
1 + 0,4545 =
b) Transformamos a parte decimal em fração Geratriz de uma Dizima Periódica Simples:
1 + 45/99 =
c) Somamos usando o M.M.C:
(99 + 45)/99 = 144/99
Encontramos a fração geratriz.
Dica: Revise diferentes maneiras de encontrar o Mínimo Múltiplo Comum para acelerar a resolução de exercícios no Enem e nos vestibulares. Veja este resumo da professora Wânia para o Curso Enem Gratuito.
III. Fração Geratriz de uma Dízima Periódica Composta:
As dízimas compostas são convertidas em fração através de um método prático que forma a fração. Veja o passo-a-passo:
a) Para cada algarismo do período ainda se coloca um algarismo 9 no denominador.
b) Para cada algarismo do antiperíodo se coloca um algarismo zero, também no denominador.
Atenção! O antiperíodo é formado pelos algarismos antes do período.
c) Calcule o denominador do seguinte modo:
![]()
Observe o exemplo: Determine a fração Geratriz da Dízima Periódica Composta:
a)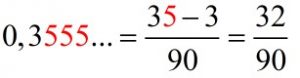
O período da Dízima Periódica Composta é 5 e o antiperíodo é 3.
Sendo assim, a fração geratriz é 32/90.
b)
O período da Dízima Periódica Composta é 2 e o antiperíodo é 25.
Dessa maneira, a fração geratriz é 227/90.
E aí, conseguiu aprender tudo sobre dízima periódica? Beleza! Assista ao vídeo do nosso canal para aprender de uma outra forma, com o professor Sérgio Sarkis, como resolver as questões com dízimas periódicas!
Resumindo
- Você aprendeu que as dízimas podem ser classificadas em finitas e em infinitas.
- Também podem ser periódicas que fazem parte do conjunto dos números racionais e as não-periódicas estão no conjunto dos números Irracionais.
- As dízimas periódicas podem ser simples ou compostas e podemos determinar sua fração geratriz.
Agora, para ver se você aprendeu tudo o que vimos aqui, resolva as questões que selecionei para você:
- (ENEM) Um estudante se cadastrou numa rede social na internet que exibe o índice de popularidade do usuário. Esse índice é a razão entre o número de admiradores do usuário e o número de pessoas que visitam seu perfil na rede. Ao acessar seu perfil hoje, o estudante descobriu que seu índice de popularidade é 0,3121212…
O índice revela que as quantidades relativas de admiradores do estudante e pessoas que visitam seu perfil são
A) 103 em cada 330.
B) 104 em cada 333.
C) 104 em cada 3 333.
D) 139 em cada 330.
E) 1 039 em cada 3 330.
- (UFAC) Sejam x e y dois números reais. Sendo x = 2,333… e y = 0,1212…, dízimas periódicas. A soma das frações geratrizes de x e y é:
A) 7/3.
B) 4/33.
C) 27/11.
D) 27/33.
E) 27/3.
- (PUC – RJ) A soma 1,3333… + 0,1666666… é igual a:
A) 1/2
B) 5/2
C) 4/3
D) 5/3
E) 3/2
Gabarito: 1 – A, 2 – C, 3 – E.





