Função do 1º grau: exercícios resolvidos
Confira a resolução de duas questões do Enem sobre função do 1º grau e, em seguida, treine com a nossa lista de exercícios!
A função do 1º grau (ou função afim) é um daqueles conteúdos que você não pode deixar de estudar para o Enem. Isso porque, em quase todos as edições, cai pelo menos uma questão sobre o tema. Por isso, o Lucas Borguezan, nosso professor de Matemática, vai te ensinar a resolver dois exercícios que já caíram nas provas.
Primeiramente vamos resolver uma questão considerada fácil. Em seguida, partiremos para uma questão de dificuldade média. Acompanhe o conteúdo em vídeo e em texto!
Exercícios resolvidos sobre função do 1º grau
O primeiro exercício que vamos resolver caiu na 2ª aplicação do Enem 2018 e é classificado como fácil. Confira:
(ENEM MEC/2018/2ª Aplicação)
Uma indústria automobilística está testando um novo modelo de carro. Cinquenta litros de combustível são colocados no tanque desse carro, que é dirigido em uma pista de testes até que todo o combustível tenha sido consumido. O segmento de reta no gráfico mostra o resultado desse teste, no qual a quantidade de combustível no tanque é indicada no eixo y (vertical), e a distância percorrida pelo automóvel é indicada no eixo x (horizontal).

A expressão algébrica que relaciona a quantidade de combustível no taque e a distância percorrida pelo automóvel é
a) y = -10x + 500
b) ![]()
c) ![]()
d) ![]()
e) ![]()
Resolução em vídeo
Para ver o professor Lucas resolvendo essa questão e a próxima, confira o vídeo do nosso canal. Em seguida, você encontra o passo a passo completo em texto.
Resolução em texto
Para começar a resolver qualquer questão de Matemática, uma boa dica é destacar as informações mais importantes e que você irá utilizar na resolução. Neste exercício, podemos destacar os 50 litros de combustível e os 500 km percorridos:

Em seguida, precisamos lembrar o modelo de função afim ou de 1º grau:
f(x) = ax + b
Nesta questão, o valor de b são os 50 litros. Assim, já podemos substituir:
f(x) = ax + 50
Só com esse passo já eliminamos as alternativas (a), (c) e (e). Mas, ainda precisamos descobrir qual é o valor de a.
Para isso, precisamos de um novo ponto no gráfico, sem ser do 50 que está no eixo y. Por isso, vamos utilizar o 500 km, cuja posição é (500, 0). Ou seja, ele está na posição 500 no eixo x e 0 no eixo y. Para utilizar esse ponto na função, realizamos o seguinte passo a passo:
- Substituímos o f(x) pelo valor de x;
- Substituímos x por 500;
- Invertemos ax e obtemos 500a.
Portanto, a função fica assim:
0 = 500a + 50
Em seguida, separamos as letras dos números:
-50 = 500a
Agora, basta passar o 500 para o outro lado divindo:
-50/500 = a
-1/10 = a
Por fim, é só substituir o valor de a na função:
f(x) = -1/10 x + 50
A alternativa correta está presente na questão, mas está escrita de forma diferente: -x/10 + 50. Isso porque é como se o número 1 estivesse escondido entre o sinal de menos e o x. Portanto, a alternativa correta é a letra (b).
Em seguida, vamos resolver uma questão de função do 1º grau que caiu no Enem Digital 2020 e tem dificuldade média. Confira:
(ENEM MEC/2020/Aplicação Digital)
Por muitos anos, o Brasil tem figurado no cenário mundial entre os maiores produtores e exportadores de soja. Entre os anos de 2010 e 2014, houve uma forte tendência de aumento da produtividade, porém, um aspecto dificultou esse avanço: o alto custo do imposto ao produtor associado ao baixo preço de venda do produto. Em média, um produtor gastava R$ 1200,00 por hectare plantado, e vendia por R$ 50,00 cada saca de 60 kg. Ciente desses valores, um produtor pode, em certo ano, determinar uma relação do lucro L que obteve em função das sacas de 60 kg vendidas. Suponha que ele plantou 10 hectares de soja em sua propriedade, na qual colheu x sacas de 60 kg e todas as sacas foram vendidas.
Disponível em: www.cnpso.embrapa.br. Acesso em: 27 fev. 2012 (adaptado).
Qual é a expressão que determinou o lucro L em função de x obtido por esse produtor nesse ano?
a) L(x) = 50x – 1 200
b) L(x) = 50x – 12 000
c) L(x) = 50x + 12 000
d) L(x) = 500x – 1 200
e) L(x) = 1 200x – 500
Resolução
Em seguida vamos resolver a questão, mas não esqueça que as instruções também estão no vídeo do início do post.
Primeiramente, destacamos os valores que iremos utilizar na resolução da questão:
- Custo da produção por hectare: R$ 1.200.
- Valor de cada saca vendida: R$50.
Em seguida, vamos calcular o custo total que o produtor de soja teve. Para isso, multiplicamos o custo (R$1.200) pelo número de hectares (10).
Ao mesmo tempo, precisamos calcular o valor que ele obteve com as vendas. Assim, multiplicamos o valor da saca (R$ 50) pelo número de sacas vendidas (x) – que não é fornecido pela questão, e por isso, representamos como x.
Assim, podemos montar uma expressão algébrica calculando os ganhos menos o custo fixo:
50 . x – 1200 . 10
Essa é, nada mais, nada menos, do que a maneira de calcular o lucro. Dessa forma, podemos montar a equação completa:
L(x) = 50x – 12.000
Portanto, a letra (b) é a alternativa correta.
Exercícios sobre função do 1º grau
Para continuar seus estudos e testar o que aprendeu, resolva a lista de exercícios sobre função do 1º grau:
Sumário do Quiz
0 de 10 questões completadas
Perguntas:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
Information
.
Você já fez este questionário anteriormente. Portanto, não pode fazê-lo novamente.
Quiz is loading...
You must sign in or sign up to start the quiz.
Para iniciar este questionário, você precisa terminar, antes, este questionário:
Resultados
0 de 10 perguntas respondidas corretamente
Seu tempo:
Acabou o tempo
Você conseguiu 0 de 0 pontos possíveis (0)
| Pontuação média |
|
| Sua pontuação |
|
Categorias
- Sem categoria 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- Respondido
- Revisão
-
Pergunta 1 de 10
1. Pergunta
(UNCISAL/2019)
A empresa onde Antônio trabalha contratou uma instituição que oferece planos de saúde. De acordo com o contrato, o valor da mensalidade I(r) a ser pago pelos empregados ao plano de saúde está vinculado à renda mensal — r, em mil reais — de cada um deles, conforme a posição nos intervalos do eixo horizontal no gráfico a seguir. Para um empregado com renda inferior a R$ 5 000,00, a própria empresa custeará o plano de saúde. Para os demais, a mensalidade do plano seguirá os intervalos de valores indicados no gráfico, de modo que, por exemplo, 0,2r significa que a mensalidade do plano será igual à renda no intervalo correspondente multiplicada pelo fator 0,2.
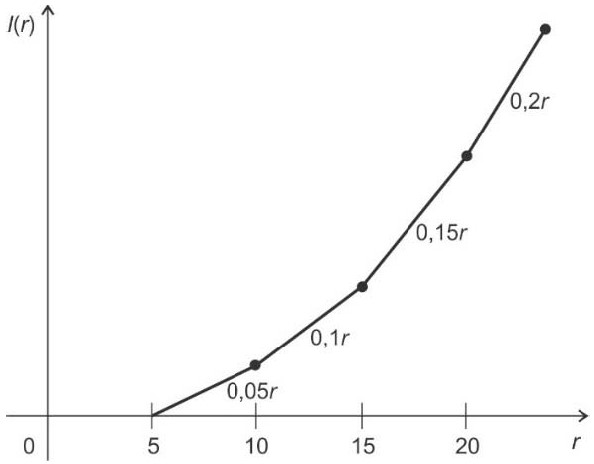
Se a renda mensal de Antônio é R$ 11 000,00, qual será o percentual que ele pagará pelo plano de saúde?
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre função de 1º grau para acertar na hora da prova!
-
Pergunta 2 de 10
2. Pergunta
(UERJ/2019)
A população de uma espécie animal fica multiplicada pelo mesmo fator após intervalos de tempo iguais. No período de 1984 a 1996, essa população passou de 12500 para 25000 indivíduos. Considere que, para o mesmo intervalo de tempo nos anos seguintes, o fator permanece constante.
O número de indivíduos dessa população em 2032 será aproximadamente igual a:
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre função de 1º grau para acertar na hora da prova!
-
Pergunta 3 de 10
3. Pergunta
(UNIFOR CE/2019)
Uma distribuidora de alimentos funciona de segunda à sexta-feira das 08:00 às 18:00. Às 8h de segunda-feira, a empresa tinha em seu estoque 42 toneladas de alimentos. Nesse dia, a empresa enviou 8 toneladas e recebeu 5. Na terça-feira, enviou 12 toneladas e não recebeu carregamento algum. Na quarta-feira, enviou 9 toneladas e recebeu 15. Na quinta-feira, enviou 8 toneladas e recebeu 11. Na sexta-feira, enviou 3 toneladas e recebeu 7. Qual dos gráficos representa a quantidade de alimentos (em toneladas) no estoque da empresa no final de cada dia?
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre função de 1º grau para acertar na hora da prova!
-
Pergunta 4 de 10
4. Pergunta
(UERJ/2018)
Os veículos para transporte de passageiros em determinado município têm vida útil que varia entre 4 e 6 anos, dependendo do tipo de veículo. Nos gráficos está representada a desvalorização de quatro desses veículos ao longo dos anos, a partir de sua compra na fábrica.
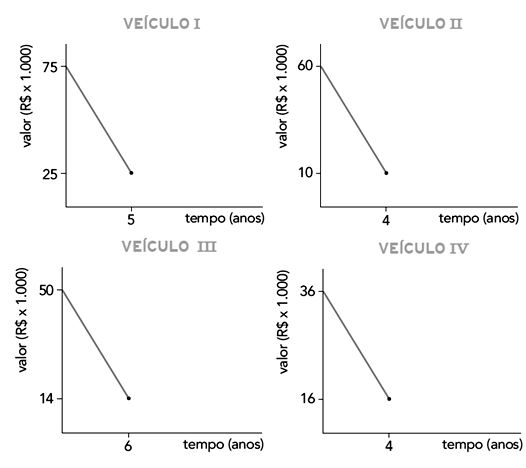
Com base nos gráficos, o veículo que mais desvalorizou por ano foi:
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre função de 1º grau para acertar na hora da prova!
-
Pergunta 5 de 10
5. Pergunta
(FATEC SP/2018)
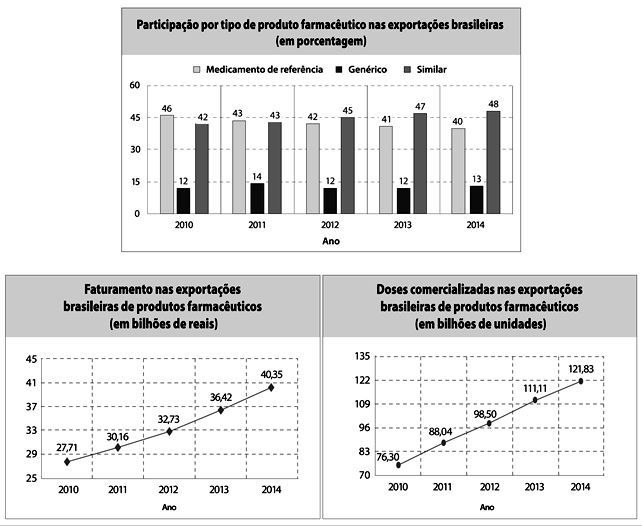
<https://tinyurl.com/yaevl4u9> Acesso em: 25.02.2018. Adaptado. No período de 2010 a 2014, o crescimento no número de doses comercializadas, em bilhões de unidades, é aproximadamente linear.
Se o crescimento observado de 2010 a 2014 se mantiver nos próximos anos, o número de doses comercializadas em 2018, em bilhões de unidades, será, aproximadamente,
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre função de 1º grau para acertar na hora da prova!
-
Pergunta 6 de 10
6. Pergunta
(UNITAU SP/2018)
Em um determinado estado brasileiro, no final de 2012, o número de pessoas infectadas pela febre amarela era igual a 324 e, no final de 2017, esse número passou para 859 pessoas. Admitindo que o número de pessoas infectadas cresce linearmente com o tempo, podemos afirmar que, no final de 2018, o número de pessoas infectadas será igual a
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre função de 1º grau para acertar na hora da prova!
-
Pergunta 7 de 10
7. Pergunta
(UNICESUMAR PR/2018)
Seja f uma função de R em R, sendo R o conjunto dos números reais, definida por f(x) = 2x – 13, os valores de x pertencentes ao domínio dessa função e que produzem imagens maiores que 7 são tais que
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre função de 1º grau para acertar na hora da prova!
-
Pergunta 8 de 10
8. Pergunta
(UEG GO/2018)
A função que descreve o lucro mensal L de um comerciante, em função da quantidade x de produtos vendidos mensalmente, é representada pelo gráfico a seguir.
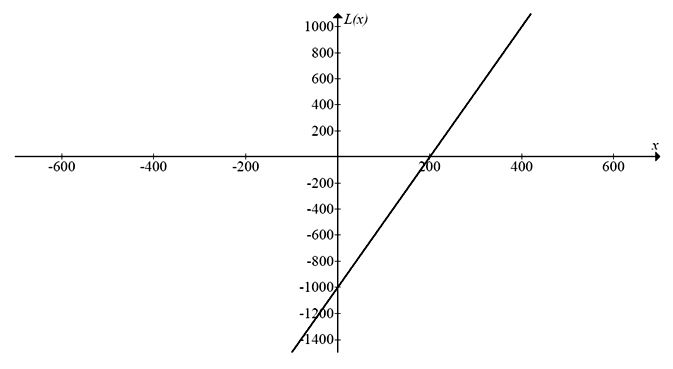
Analisando-se o gráfico, a quantidade de produtos que esse comerciante tem que vender para obter um lucro de exatamente R$ 2.000,00 é de
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre função de 1º grau para acertar na hora da prova!
-
Pergunta 9 de 10
9. Pergunta
(UFGD MS/2018)
Uma pesquisa sobre o Panorama dos Resíduos Sólidos no Brasil no ano de 2014, realizada pela Abrelpe (Associação Brasileira de Empresas de Limpeza Pública e Resíduos Especiais), apontou que os 467 municípios dos três estados da região Centro-Oeste e o Distrito Federal geraram, em 2014, a quantidade de 16.948 toneladas/dia de RSU (Resíduos Sólidos Urbanos), das quais 93,4% foram coletadas. Os dados indicam um crescimento de 2,2% no total coletado e um aumento de 1,9% na geração de RSU em relação ao ano anterior. A tabela a seguir apresenta os dados coletados e gerados de RSU no estado de Mato Grosso do Sul.
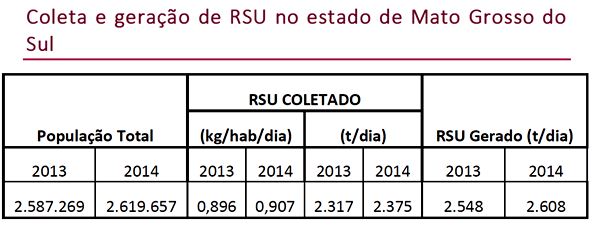
Fonte: Pesquisa ABRELPE e IBGE. Disponível em http://www.abrelpe.org.br/Panorama/panorama2014.pdf . Acesso em: 14 out. 2017 Supondo que a quantidade de RSU gerada no MS em t/dia seja uma função afim, é correto afirmar que a previsão de RSU a ser gerada em 2020 em t/dia será de
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre função de 1º grau para acertar na hora da prova!
-
Pergunta 10 de 10
10. Pergunta
(UFRGS/2018)
Para produzir determinado tipo de tecido, uma fábrica gasta R$ 2,20 por metro. Além disso, há uma despesa fixa de R$ 2.500,00, independente da quantidade de metros produzidos. Se cada metro do tecido é vendido por R$ 4,00, o número mínimo de metros no qual a fábrica passa a ter lucro com a venda é
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre função de 1º grau para acertar na hora da prova!

Sobre o(a) autor(a):
Lucas Borguezan2 - Lucas Borguezan é matemático formado pela Universidade Federal de Santa Catarina. Ministra aulas de matemática para turmas desde os 18 anos de idade e tenta sempre encontrar métodos atualizados e alternativos de se ensinar matemática usando tecnologia.
Gostou? Compartilhe!
Continue lendo:
Aqui vão 2 publicações relacionadas que talvez você goste:

Como resolver a prova de Matemática no Enem 2024? Veja as dicas do professor
Por Melina Zanotto | 08 de novembro
Confira as orientações e estratégias do professor Lucas Borguezan para se sair bem na prova de Matemática no Enem 2024.

Aulão Enem de Matemática: revisão intensiva e gratuita para a prova
Por João Vianney dos Valles Santos | 11 de outubro
Assista ao Aulão Enem de Matemática do Curso Enem Gratuito e revise os conteúdos mais importantes para a prova.

