Uma função qualquer pode ser definida por duas ou mais sentenças, assim isso vale também para a função modular. Módulo e função modular servem para expressar o conceito de distância negativa.
Você já deve ter reparado que toda a vez que você resolve uma equação e o enunciado se trata de uma medida de comprimento, o resultado que você obtém precisa ser positivo. Anote aí no cérebro, que tem tudo a ver com a função modular. Além disso, em casos em que temos dois resultados, como em uma fórmula de Bhaskara, ao se tratar de distâncias “escolhemos” apenas o resultado positivo.
Você sabe por que isso acontece? Simplesmente porque uma distância nunca pode ser negativa. Imagine você andando por 300 metros: existe a possibilidade de andar 300 metros negativos? É para expressar esse conceito de distância negativa que surgiram o módulo e a função modular.
O que é módulo?
O módulo de um número real surgiu da necessidade de medir a distância de um número negativo até o zero. Mas, na verdade, a definição do módulo é que expressa o conceito de distância.
Introdução à Função Modular
Veja agora com o professor de matemática Lucas Borguezan, do canal do curso Enem Gratuito, um resumo para você lembrar ou aprender a Função Modular. Aprenda a resolver questões e elaborar os gráficos.
Matematicamente falando, o módulo é a distância de um determinado número da reta real (independente se for negativo ou positivo) até o zero.
Sendo assim, o módulo de um número real sempre será positivo, pois a distância sempre será positiva.
Como um exemplo, a distância de – 3 até o 0 é 3 u.c.:
Então:
|- 3 | = 3
Da mesma forma, a distância de 5 até 0 é 5 u.c.
Então:
| 5 | = 5
Por definição, podemos dizer que:
|x| = x, se x ≥ 0 (positivo)
-x, se x < 0 (negativo)
Para entendermos melhor, vamos ver exemplos:
Exemplos de módulo:
Calcule o valor de x na equação |2x – 1| = 9
Para que os dois lados da equação sejam equivalentes, significa que o que está dentro do módulo deve ser igual a 9 ou igual a – 9.
Dessa forma: 2x – 1 = 9 ou 2x – 1 = – 9
Assim 2x = 9 + 1 2x = – 9 +1
Portanto 2x = 10 2x = – 8
x = 5 x = -4
Isso quer dizer que tanto para x = 5 quanto para x = – 4, a equação |2x – 1| = 9 é verdadeira. O conjunto solução se apresenta da forma:
S = { -4, 5 }
Exemplo 2:
Quais são as possíveis soluções da equação | 5x-6 | = x² ?
Segundo a definição: temos que 5x – 6 = x² ou 5x-6 = -x². Resolvendo cada uma das equações:
f5x – 6 = x²
x² – 5x + 6 = 0
S = -5 , P = 6
(x-2)(x-3) = 0
x = 2 ou x = 3
5x – 6 = -x²
x² + 5x – 6 = 0
S = 5, P = -6
(x+6)(x-1) = 0
x = -6 ou x = 1
Assim, teremos quatro soluções, S = { – 6 , 1, 2, 3 }
Função Modular
Uma função qualquer pode ser definida por duas ou mais sentenças. Isso vale também para a função modular, ela apresenta a característica do valor absoluto. Para definir uma função modular basta levar em consideração que para cada valor escolhido de x existirá uma f(x) = |x| onde:
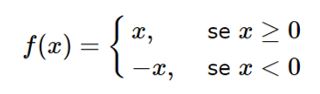
Então, para a função modular, temos duas possibilidades: quando a função está positiva ela permanece positiva, e quando a função que está no módulo for negativa, inverte-se o sinal da função.
Isso significa que, no gráfico, para todos os valores negativos de x a função que está em módulo não assumirá valores de y. Ou seja, não assume valores na Imagem porque o domínio não está definido. Vejamos como fica a simples função do enunciado representada graficamente:
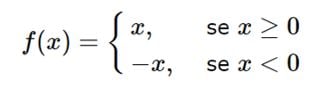
Portanto, atribuindo valores para x, encontramos o valor correspondente á f(x):
| x | f(x) = y |
| -2 | – ( – 2) |
| -1 | – ( – 1) |
| 0 | 0 |
| 1 | 1 |
| 2 | 2 |
Substituindo os valores no plano cartesiano:
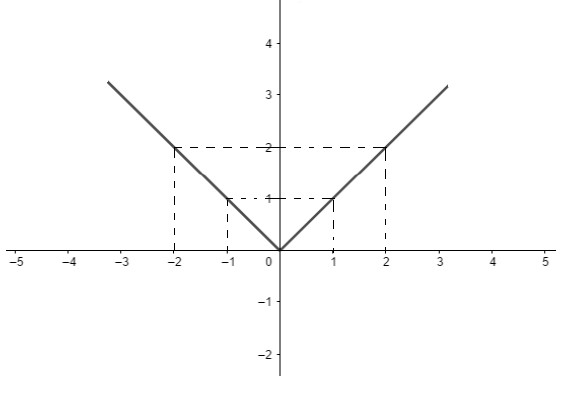
Perceba que, como não é possível obter valores negativos para a imagem, o gráfico não avança para valores negativos de y. Mas, cuidado! Nem toda função que apresenta módulo em sua composição será dessa forma! Afinal, só o que está dentro do módulo deixa de assumir valores negativos, o que está fora do módulo ainda pode assumir. Entenda isso com o exemplo abaixo:
Função modular resolvida
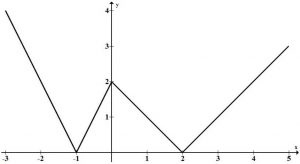
Vamos determinar o gráfico de f(x) = |x +1| – 2.
S: para solucionar questões como essa devemos seguir alguns passos. Primeiro fazemos o estudo do sinal da função que está dentro do módulo, encontrando a raiz. Então
x + 1 = 0
x = -1
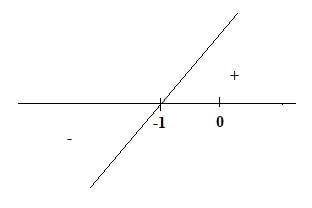
Assim, para todos os valores de 
a função f(x) = |x +1| – 2 pode ser reescrita como:
f(x) = x + 1 – 2
f(x) = x -1
(os valores de dentro do módulo mantiveram seu sinal)
Já para os valores de 
a função f(x) = |x +1| – 2 se transforma em:
f(x) = – ( x+1) -2
Assim, f(x) = – x -1 – 2
Portanto: f(x) = – x – 3
Escrevendo a função definida por duas sentenças, a fim de organização, tem-se:
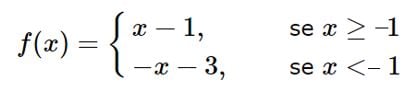
Para o gráfico da função modular, fazemos da mesma forma, atribuindo valores para x e encontrando seu correspondente em y.
| x | f(x) = y |
| -2 | -1 |
| -1 | -2 |
| 0 | -1 |
| 1 | 0 |
| 2 | 1 |
Dessa forma, atribuímos os valores ao plano cartesiano:
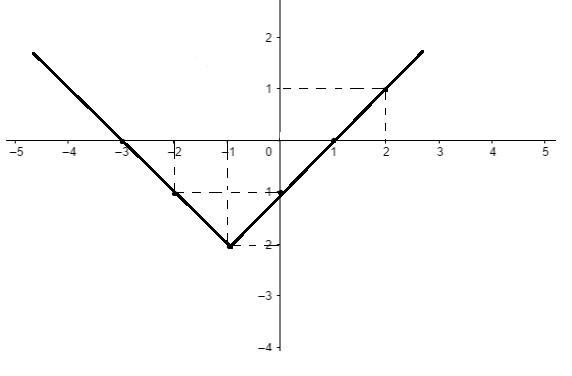
Perceba como o gráfico possui valores negativos para a imagem, mesmo possuindo módulo na função, isso se dá pelo fato de o – 2 em f(x) = |x +1| – 2 indicar que o gráfico inteiro se desloca duas unidades para baixo do eixo x.
Resumo de Módulo e Inequação
Exercícios de função modular
Por fim, resolva os exercícios sobre função modular e prepare-se para suas provas!
.
formam um conjunto que:
