Função de 2º grau ou quadrática: veja como resolver

Um dos estudos mais importantes nas ciências exatas é o estudo da função quadrática ou de 2º grau e sua parábola. Esse tema é questão certa na prova de matemática dos vestibulares e do Enem. Veja como resolver com a Fórmula de Bhaskara

O que é uma função de 2º grau

Podemos dizer que uma função de 2º grau ou função quadrática é a função que obedece a seguinte formação:

Um exemplo dessa função é 

A Fórmula de Bhaskara – Como resolver Função de 2º grau

Confira agora com o professor Lucas Borguezam, do canal do Curso Enem Gratuito, como você pode resolver de maneira simples e rápida uma questão de Funções de 2º grau com a Fórmula de Bhaskara:

Os gráficos das funções

Esse tipo de função tem um gráfico chamado parábola que tem algumas características que precisamos entender bem.

Os principais pontos para o estudo gráfico da parábola são:

• • Sinal do coeficiente a: se o sinal desse coeficiente for positivo a concavidade da parábola estará voltada para cima. Se o coeficiente a for negativo, a concavidade estará voltada para baixo.
  • Raízes da função: obtemos as raízes fazendo f(x) = y = 0. Neste caso definimos os pontos onde a parábola intercepta o eixo x.
  • Para o cálculo das raízes usamos a fórmula de Bhaskara:

• Vértice da parábola: o vértice é definido pelas seguintes fórmulas:

• Intersecção com o eixo y: neste caso o valor de x é igual a zero e y = c.
• Imagem: seu estudo está relacionado à concavidade da parábola e se o vértice será um ponto de máximo (concavidade voltada para baixo) ou ponto de mínimo (concavidade da parábola voltada para cima).

Como representadas nas figuras abaixo: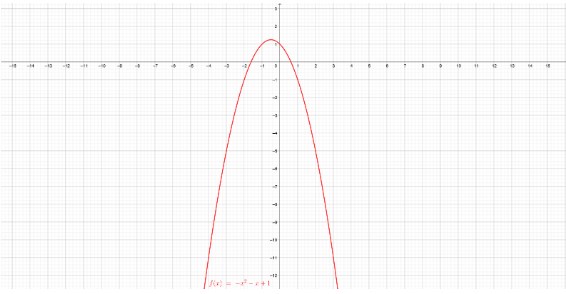Representação gráfica de uma parábola com a concavidade voltada para baixo. Fonte: Autora (2018) com Geogebra

Agora, veja com a parábola invertida: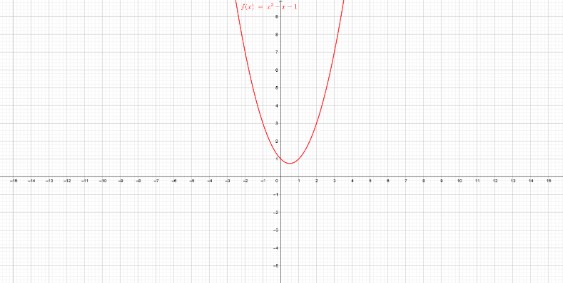Parábola em vermelho com concavidade voltada para cima. Fonte: Autora (2018) com Geogebra

Confira com o professor Sërgio Sarkis outra explicação sobre a Fórmula de Bhaskara:

.

Estudo do sinal do gráfico da função de 2º grau ou função quadrática:

Para analisarmos os sinais desse tipo de função é preciso verificar os intervalos do domínio onde tem a imagem positiva, negativo ou igual a zero.

Além disso, não podemos esquecer de ver o sinal do coeficiente a e do valor do delta.

Veja o resumo abaixo caso a caso: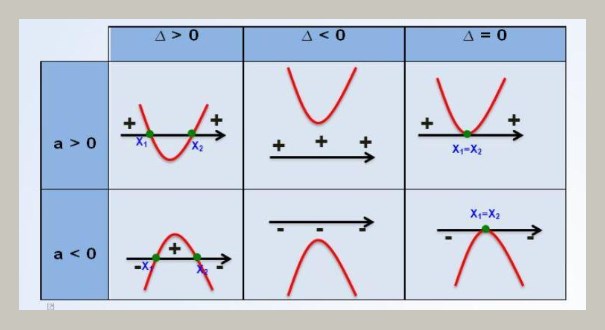Quadro resumo com desenhos das parábolas em vermelho e com seus sinais. Fonte: http://slideplayer.com.br/slide/3229257/11

Como analisar essa tabela:

Se tivermos:

• os valores menores que x1 e os valores maiores que x2 o sinal será positivo. Entre x1 e x2 o sinal será negativo.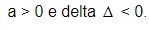
• O sinal será positivo sempre.
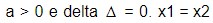• e o sinal será positivo para menores que x1 e maiores que x2.
• o sinal será positivo entre x1 e x2.
• o sinal será negativo sempre.
• o sinal será negativo fora do lado externo da concavidade.

Lembramos que delta é dado através da fórmula:

Agora que já mostramos todas as regras para você, que tal um exemplo prático?

Vamos a ele:

Vamos ao estudo da função da forma

Se quisermos construir uma parábola precisamos definir os seguintes itens:

a) Os coeficientes dessa função: 

b) Calcular as raízes dessa função: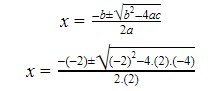

Fazendo os cálculos temos:

Então temos os dois pontos onde a parábola irá cortar o eixo x. Os pares ordenados são B ( 2, 0) e C (-1, 0).

c) Precisamos calcular o Vértice da parábola: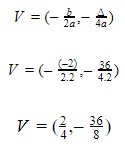

Simplificando as frações temos: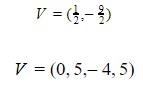

Como a parábola tem concavidade para cima, o vértice é um ponto de mínimo.

d) A imagem da função é dada pelo valor de y para o vértice, então o conjunto imagem será:

Já podemos também definir o ponto onde a parábola irá cortar o eixo y: nesse caso x = 0 e y = c, isto é, y = – 4. E o par ordenado será dado por A (0, – 4).

Colocando todos os pares ordenados no plano cartesiano temos: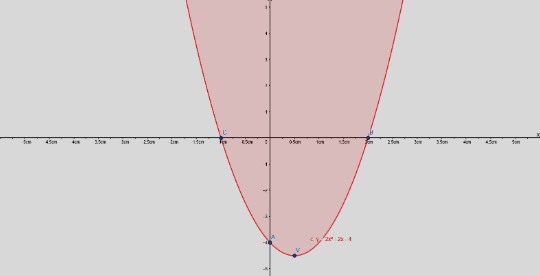Parábola construída com os pares ordenados calculados no exemplo. Fonte: Autora (2018) com Geogebra

Videoaula sobre função de 2º grau

Agora é com você! Simule vários gráficos de outras funções de 2º grau no app Geogebra. É um software livre de fácil entendimento e você visualiza a construção do gráfico através dos pares ordenados ou da função. Vai lá, instala em seu smartphone, tablet, IOS ou PC.

Exercícios

Limite de tempo: 0

Sumário do Quiz

0 de 10 questões completadas

Perguntas:

1. 1
2. 2
3. 3
4. 4
5. 5
6. 6
7. 7
8. 8
9. 9
10. 10

Information

.

Você já fez este questionário anteriormente. Portanto, não pode fazê-lo novamente.

Quiz is loading...

You must sign in or sign up to start the quiz.

Para iniciar este questionário, você precisa terminar, antes, este questionário:

Resultados

0 de 10 perguntas respondidas corretamente

Seu tempo:

Acabou o tempo

Você conseguiu 0 de 0 pontos possíveis (0)

Pontuação média
Sua pontuação

Categorias

1. Sem categoria 0%

Registrar seu resultado no ranking de pontuações

Carregando

Nome: E-Mail:

Captcha:

1. 1
2. 2
3. 3
4. 4
5. 5
6. 6
7. 7
8. 8
9. 9
10. 10

1. Respondido
2. Revisão

1. Pergunta 1 de 10

   1. Pergunta

   (UEG GO/2019)    

   Em um jogo de futebol, um jogador chuta uma bola parada, que descreve uma parábola até cair novamente no gramado. Sabendo-se que a parábola é descrita pela função y = 20x – x², a altura máxima atingida pela bola é

   • 100 m
   • 80 m
   • 60 m
   • 40 m
   • 20 m
   Correto
   

   Parabéns! Siga para a próxima questão.

   Incorreto
   

   Resposta incorreta. Revise o conteúdo nesta aula sobre função quadrática ou de 2º grau para acertar na hora da prova!
2. Pergunta 2 de 10

   2. Pergunta

   (UNICAMP SP/2019)    

   Sejam a e b números reais positivos. Considere a função quadrática f (x) = x (ax + b), definida para todo número real x. No plano cartesiano, qual figura corresponde ao gráfico de y = f (x)?

   • 
   • 
   • 
   • 
   Correto
   

   Parabéns! Siga para a próxima questão.

   Incorreto
   

   Resposta incorreta. Revise o conteúdo nesta aula sobre função quadrática ou de 2º grau para acertar na hora da prova!
3. Pergunta 3 de 10

   3. Pergunta

   (UFT TO/2019)    

   Ao realizar o estudo de sua produção diária, uma cozinheira que faz e vende pamonhas, descobriu que o lucro em reais é calculado pela função 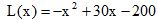onde x é o número de pamonhas feitas e vendidas. Com base nestas informações, é CORRETO afirmar que o lucro máximo diário da cozinheira é:

   • R$ 10,00
   • R$ 15,00
   • R$ 20,00
   • R$ 25,00
   Correto
   

   Parabéns! Siga para a próxima questão.

   Incorreto
   

   Resposta incorreta. Revise o conteúdo nesta aula sobre função quadrática ou de 2º grau para acertar na hora da prova!
4. Pergunta 4 de 10

   4. Pergunta

   (Faculdade Santo Agostinho BA/2018)    

   Um fabricante vende, mensalmente, x unidades de um determinado artigo. O lucro desse fabricante foi modelado, matematicamente, através da função f, dada por f (x) = –x² + 16x – 7. Quantas unidades desse artigo devem ser vendidas, mensalmente, para que o lucro do fabricante seja máximo?

   • 10.
   • 16.
   • 8.
   • 4.
   Correto
   

   Parabéns! Siga para a próxima questão.

   Incorreto
   

   Resposta incorreta. Revise o conteúdo nesta aula sobre função quadrática ou de 2º grau para acertar na hora da prova!
5. Pergunta 5 de 10

   5. Pergunta

   (FPS PE/2018)    

   A frequência máxima de batimento cardíaco de um indivíduo, FC_max, em batimentos por minuto, depende da idade, x, do indivíduo, dada em anos. Um estudo concluiu que a relação entre FC_max e x é dada por uma função quadrática:

   FC_max = 163 + 1,16x – 0,018x²

   Admitindo a veracidade do estudo, para qual idade temos que FC_max assume seu maior valor? Indique o valor inteiro mais próximo do valor obtido, em anos.

   • 31 anos
   • 32 anos
   • 33 anos
   • 34 anos
   • 35 anos
   Correto
   

   Parabéns! Siga para a próxima questão.

   Incorreto
   

   Resposta incorreta. Revise o conteúdo nesta aula sobre função quadrática ou de 2º grau para acertar na hora da prova!
6. Pergunta 6 de 10

   6. Pergunta

   (UNITAU SP/2018)    

   Sobre o gráfico da função definida no conjunto dos números reais por f(x) = 2x² – 4x – 6, pode-se afirmar, CORRETAMENTE, que

   • sua concavidade é voltada para baixo.
   • intercepta o eixo das abscissas em x = 1.
   • intercepta o eixo das ordenadas em y = 6 .
   • tem seu ponto de mínimo em x = 1.
   • tem seu vértice no terceiro quadrante.
   Correto
   

   Parabéns! Siga para a próxima questão.

   Incorreto
   

   Resposta incorreta. Revise o conteúdo nesta aula sobre função quadrática ou de 2º grau para acertar na hora da prova!
7. Pergunta 7 de 10

   7. Pergunta

   (Mackenzie SP/2018)    

   Se f (x) = ax² + bx + c é tal que f (2) = 8, f (3) = 15 e f (4) = 26, então a + b + c é igual a

   • 5
   • 4
   • 3
   • 2
   • 1
   • 6
   Correto
   

   Parabéns! Siga para a próxima questão.

   Incorreto
   

   Resposta incorreta. Revise o conteúdo nesta aula sobre função quadrática ou de 2º grau para acertar na hora da prova!
8. Pergunta 8 de 10

   8. Pergunta

   (UNIRG TO/2018)    

   Em um terreno, deseja-se fazer uma cerca retangular usando-se tela em três lados do retângulo. Sabendo-se que são necessários 500 metros de tela para cercar o terreno, a função que representa a área A a ser cercada em função da medida x do lado será dada por:

   • A = 250x – 0,5x2;
   • A = 300x – 0,5x2;
   • A = 250x – x2;
   • A = 300x – x2.
   Correto
   

   Parabéns! Siga para a próxima questão.

   Incorreto
   

   Resposta incorreta. Revise o conteúdo nesta aula sobre função quadrática ou de 2º grau para acertar na hora da prova!
9. Pergunta 9 de 10

   9. Pergunta

   (Universidade Iguaçu RJ/2018)    

   Um forno autoclave é pré-aquecido e mantém sua temperatura constante. Admitindo-se que a temperatura de pré-aquecimento, em graus centígrados, é dada por F(t) = 25 + 20t, se 0  t < 5 e F(t) = t² + 10t + 50, se 5 ≤ t ≤ 15, em que o tempo t é dado em minutos, é correto afirmar que o tempo necessário para que o autoclave passe de 85ºC para 194ºC é de

   • 5 min.
   • 6 min.
   • 7 min.
   • 8 min.
   • 9 min.
   Correto
   

   Parabéns! Siga para a próxima questão.

   Incorreto
   

   Resposta incorreta. Revise o conteúdo nesta aula sobre função quadrática ou de 2º grau para acertar na hora da prova!
10. Pergunta 10 de 10

    10. Pergunta

    (ENEM/2018)    

    Um projétil é lançado por um canhão e atinge o solo a uma distância de 150 metros do ponto de partida. Ele percorre uma trajetória parabólica, e a altura máxima que atinge em relação ao solo é de 25 metros.

    

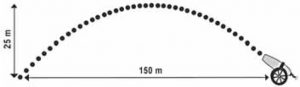
    Admita um sistema de coordenadas xy em que no eixo vertical y está representada a altura e no eixo horizontal x está representada a distância, ambas em metro. Considere que o canhão está no ponto (150; 0) e que o projétil atinge o solo no ponto (0; 0) do plano xy.

    A equação da parábola que representa a trajetória descrita pelo projétil é

    • y = 150x – x2
    • y = 3 750x – 25x2
    • 75y = 300x – 2x2
    • 125y = 450x – 3x2
    • 225y = 150x – x2
    Correto
    

    Parabéns! Siga para a próxima questão.

    Incorreto
    

    Resposta incorreta. Revise o conteúdo nesta aula sobre função quadrática ou de 2º grau para acertar na hora da prova!

Referências bibliográficas

IEZZI, Gelson. Matemática, Ciência e Aplicações. São Paulo. Ed. Saraiva. 2010.

MACHADO, Antonio. Volume Único: Ensino Médio. São Paulo: Atual, 2012.

TINANO, Marilene. Matemática 9º ano – Belo Horizonte: Ed. Educacional, 2015.

Compartilhe: