Função Logarítmica
As funções logarítmicas têm um papel bem importante na construção do conhecimento. Elas são utilizadas, por exemplo, para expressar crescimentos ou quedas populacionais. Acompanhe esta aula e, ao final, teste seus conhecimentos com os exercícios!
Podemos aplicar função logarítmica na sociologia, na biologia, na física, na química e em tantas outras disciplinas. Sendo assim, focar somente na matemática seria um erro! O estudo interdisciplinar faz você criar conexões entre as mais variadas áreas de estudo. Isso te ajuda a aumentar ainda mais seu conhecimento e desenvolver habilidades em potencial. Ora, não é porque você quer cursar medicina ou música que vai deixar de lado a matemática. Afinal, tudo está conectado!
Sendo assim, nesta aula de funções logarítmicas você vai ver algumas propriedades e maneiras de se empregar estas funções com inúmeras possibilidades de aplicação. Também vai aprender como aplicar conhecimentos de logaritmos e expoentes para solucionar as questões que envolvem esses conteúdos. Vamos lá?
O que é uma função logarítmica?
Uma função logarítmica é definida por uma lei de formação que associa cada ao número . É denominada função logarítmica de base a, onde a é real, positivo e a ≠ 1, e se apresenta na forma:
![]()
Mas, por que esse precisa ser necessariamente diferente de 1? Bem, o logaritmo de um número é definido como o expoente ao qual devemos elevar uma base a para obter o número x, ou seja,
![]()
Por esse motivo, o valor não pode assumir o valor 1, pois 1 elevado em qualquer expoente continua sendo 1. Podemos dizer que o número 1 é o elemento neutro das funções exponenciais e, portanto, também das logarítmicas.
Veja alguns exemplos de funções logarítmicas:
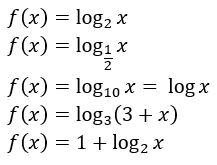
Domínio e Imagem de uma função logarítmica
O domínio de uma função representa os valores de x onde a função é definida. Ou seja, são todos os valores que x pode assumir e que resultam em um valor real para a função. Já a imagem de uma função logarítmica são todos os números reais.
Para determinar o domínio de uma função logarítmica, é preciso levar em consideração as restrições (condições de existência) dos logaritmos.
Exemplo:
Dada a função ![]()
Solução: Pela condição de existência do logaritmo, espera-se que o logaritmando ![]() seja maior do que zero (> 0). Sendo assim, resolvendo a inequação temos:
seja maior do que zero (> 0). Sendo assim, resolvendo a inequação temos:
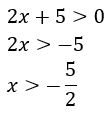
Dessa maneira, o domínio da função pode ser representado por:
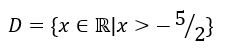
Propriedades das funções logarítmicas
O estudo das funções logarítmicas requer o conhecimento de duas propriedades. São elas:
1- As funções ![]() e
e ![]() são inversas uma da outra.
são inversas uma da outra.
Dizer que duas funções são inversas significa que uma “anula” a outra. É possível observar isso através da demonstração com função composta, observe:
![]()
Essa demonstração leva em consideração conhecimentos prévios sobre propriedades destinadas ao estudo dos logaritmos. Ela nos diz que todo logaritmo com base e logaritmandos iguais, cujo logaritmando esteja elevado em um expoente qualquer, é igual ao expoente.
2- A função logarítmica é:
- Crescente, se e somente se a > 1
- Decrescente, se e somente se 0 < a < 1
Por meio dessas propriedades podemos fazer um estudo sobre crescimento ou decrescimento. Esse estudo pode ser, por exemplo, a descrição de um fenômeno social (população), biológico (população de microrganismos) ou físico (de escoamento e vazão). Enfim, são muitos fatores que podem ser determinados através das propriedades de crescimento e decrescimento de uma função logarítmica. Vamos agora ver um exemplo de aplicação dos logaritmos em abalos sísmicos, evento da natureza que, dependendo da magnitude, pode gerar grandes estragos.
Exemplo:
(ENEM 2018) Em março de 2011, um terremoto de 9,0 graus de magnitude na escala Richter atingiu o Japão matando milhares de pessoas e causando grande destruição. Em janeiro daquele ano, um terremoto de 7,0 graus na escala Richter atingiu a cidade de Santiago Del Estero, na Argentina. A magnitude de um terremoto, medida pela escala Richter, é 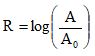 , em que A é a amplitude do movimento vertical do solo, informado em um sismógrafo, A0 é uma amplitude de referência e log representa o logaritmo na base 10.
, em que A é a amplitude do movimento vertical do solo, informado em um sismógrafo, A0 é uma amplitude de referência e log representa o logaritmo na base 10.
Disponível em: http://earthquake.usgs.gov.
Acesso em: 28 fev. 2012 (adaptado).
A razão entre as amplitudes dos movimentos verticais (A) dos terremotos do Japão e da Argentina é
a) 1,28
b) 2,0
c) ![]()
d) 100
e) 109 – 107
Solução: Para resolver a questão acima e encontrar a razão entre as amplitudes dos terremotos, primeiro iremos analisar a magnitude do terremoto do Japão e da Argentina separadamente.
Devemos levar em consideração a relação de equivalência que nos diz que:
![]()
No Japão a magnitude foi de 9,0 graus, logo, R = 9,0, assim:
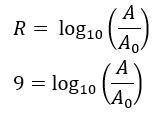
Além disso, de acordo com a relação de equivalência temos que:
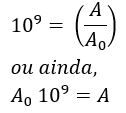 Já na Argentina, a magnitude foi de 7,0 graus, logo, R = 7,0, assim:
Já na Argentina, a magnitude foi de 7,0 graus, logo, R = 7,0, assim:
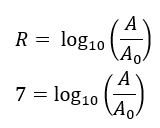
Além disso, de acordo com a relação de equivalência temos que:
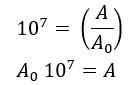 Agora, o enunciado nos pede que calculemos a razão entre as amplitudes dos movimentos verticais, assim:
Agora, o enunciado nos pede que calculemos a razão entre as amplitudes dos movimentos verticais, assim:

Sendo assim, a alternativa correta é a alternativa D.
Para complementar ainda mais seus estudos, veja essa aula do professor Ferreto
Precisa relembrar o conteúdo de logaritmos? Veja a aula de Matemática no nosso canal!
Exercícios
Sumário do Quiz
0 de 10 questões completadas
Perguntas:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
Information
.
Você já fez este questionário anteriormente. Portanto, não pode fazê-lo novamente.
Quiz is loading...
You must sign in or sign up to start the quiz.
Para iniciar este questionário, você precisa terminar, antes, este questionário:
Resultados
0 de 10 perguntas respondidas corretamente
Seu tempo:
Acabou o tempo
Você conseguiu 0 de 0 pontos possíveis (0)
| Pontuação média |
|
| Sua pontuação |
|
Categorias
- Sem categoria 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- Respondido
- Revisão
-
Pergunta 1 de 10
1. Pergunta
(UFRGS/2017)
Se log5 x = 2 e log10 y = 4, então é
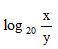 :Correto
:CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre função logarítmica para acertar na hora da prova!
-
Pergunta 2 de 10
2. Pergunta
(UNCISAL/2019)
A Escala Richter, utilizada para medir a magnitude dos terremotos, foi proposta em 1935 pelo sismólogo Charles Francis Richter, que pretendia, inicialmente, empregá-la apenas para medir abalos que ocorressem no sul da Califórnia. A equação proposta por Richter pode ser formulada de várias formas, conforme as variáveis que se adotem para compor a equação. No caso da energia mecânica liberada por um terremoto – E –, em kWh, a magnitude do terremoto – M – é expressa por
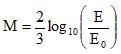 , em que E0 = 7 x 10–3 kWh.
, em que E0 = 7 x 10–3 kWh.Disponível em: http://brasilescola.uol.com.br.
Acesso em: 3 nov. 2018 (adaptado).Sabendo-se que, em 2014, um terremoto de magnitude 8 foi registrado no litoral do Alasca, qual é o valor da energia mecânica liberada nesse terremoto?
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre função logarítmica para acertar na hora da prova!
-
Pergunta 3 de 10
3. Pergunta
(IFBA/2019)
A classificação do som como forte ou fraco está relacionada ao nível de intensidade sonora, medida em watt/m2. A menor intensidade sonora audível ou limiar de audibilidade possui intensidade I0 = 10–12W/m2. A relação entre as intensidades sonoras permite calcular o nível sonoro do ambiente que é dado em decibéis. Em virtude dos valores das intensidades serem muito pequenos ou muito grandes, utiliza-se as noções de logaritmos na seguinte fórmula capaz de calcular níveis sonoros:
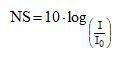
onde:
NS = Nível sonoro
I = Intensidade de som considerada
I0 = Limiar de audibilidade
Disponível em: <https://mundoeducacao.bol.uol.com.br/matematica/
medindo-intensidade-dos-sons>. Acessado em 08 de agosto de 2018.Com base no texto acima, podemos afirmar que o nível sonoro em uma avenida de tráfego intenso com intensidade de som I = 108, em W/m2, é igual a:
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre função logarítmica para acertar na hora da prova!
-
Pergunta 4 de 10
4. Pergunta
(UNIFOR CE/2018)
Desde tempos imemoriais, o homem vem buscando formas de medir e quantificar fenômenos naturais. Nesse processo, desenvolveu ferramentas físicas e abstratas para auxiliá-lo. Uma dessas ferramentas desenvolvidas foi o logaritmo na base 10, representado aqui por log. A medida da magnitude R de um terremoto, medido pela escala Richter, é
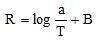 , onde a é a amplitude (em micrômetros) do movimento vertical do solo, que é informado em um sismógrafo; T é o período do abalo sísmico em segundo; e B é a amplitude do abalo sísmico, com distância crescente partindo do centro do terremoto. Em 16 de setembro de 2015, um terremoto de magnitude 8,3 atingiu o Chile, próximo a região de Valparaíso, deixando várias vítimas. Em 08 de setembro de 2017, um terremoto de magnitude 5,3 atingiu a região norte do Japão.
, onde a é a amplitude (em micrômetros) do movimento vertical do solo, que é informado em um sismógrafo; T é o período do abalo sísmico em segundo; e B é a amplitude do abalo sísmico, com distância crescente partindo do centro do terremoto. Em 16 de setembro de 2015, um terremoto de magnitude 8,3 atingiu o Chile, próximo a região de Valparaíso, deixando várias vítimas. Em 08 de setembro de 2017, um terremoto de magnitude 5,3 atingiu a região norte do Japão.Sabendo que os dois terremotos acima tiveram a mesma amplitude B e período T, podemos afirmar que o terremoto no Chile foi
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre função logarítmica para acertar na hora da prova!
-
Pergunta 5 de 10
5. Pergunta
(FGV /2018)
As funções logarítmicas f, g, h, p são dadas por f(x) = 10 + log x, g(x) = 10log x, h(x) = log(10x) e p(x) = log(x + 10). Observe os gráficos a seguir:
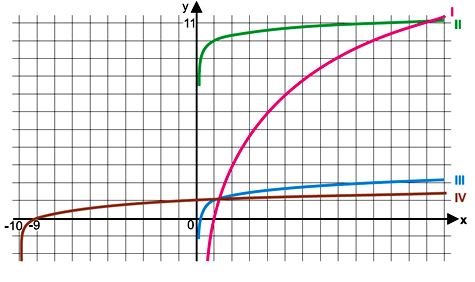
Os gráficos I, II, III e IV correspondem, respectivamente, às funções
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre função logarítmica para acertar na hora da prova!
-
Pergunta 6 de 10
6. Pergunta
(UEG GO/2018)
Considerando-se as funções f(x) = 2x e g(x) = log2 x, constata-se que
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre função logarítmica para acertar na hora da prova!
-
Pergunta 7 de 10
7. Pergunta
(UFRGS/2018)
Leia o texto abaixo, sobre terremotos.
Magnitude é uma medida quantitativa do tamanho do terremoto. Ela está relacionada com a energia sísmica liberada no foco e também com a amplitude das ondas registradas pelos sismógrafos. Para cobrir todos os tamanhos de terremotos, desde os microtremores de magnitudes negativas até os grandes terremotos com magnitudes superiores a 8.0, foi idealizada uma escala logarítmica, sem limites. No entanto, a própria natureza impõe um limite superior a esta escala, já que ela está condicionada ao próprio limite de resistência das rochas da crosta terrestre. Magnitude e energia podem ser relacionadas pela fórmula descrita por Gutenberg e Richter em 1935:
log(E) = 11,8 + 1,5M onde: E = energia liberada em Erg ; M = magnitude do terremoto.
Disponível em: <http://www.iag.usp.br/
siae98/terremoto/terremotos.htm>.
Acesso em: 20 set. 2017.Sabendo que o terremoto que atingiu o México em setembro de 2017 teve magnitude 8,2, assinale a alternativa que representa a melhor aproximação para a energia liberada por esse terremoto, em Erg.
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre função logarítmica para acertar na hora da prova!
-
Pergunta 8 de 10
8. Pergunta
(Universidade Iguaçu RJ/2018)
A população em uma cultura bacteriana, que era inicialmente de 160 bactérias, dobra a cada 3 horas.
Usando log2 52,3 se preciso, é correto descrever o tempo aproximado T (em horas) até que a população chegue a n bactérias pela função
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre função logarítmica para acertar na hora da prova!
-
Pergunta 9 de 10
9. Pergunta
(ENEM/2018)
Em março de 2011, um terremoto de 9,0 graus de magnitude na escala Richter atingiu o Japão matando milhares de pessoas e causando grande destruição. Em janeiro daquele ano, um terremoto de 7,0 graus na escala Richter atingiu a cidade de Santiago Del Estero, na Argentina. A magnitude de um terremoto, medida pela escala Richter, é
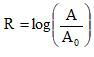 , em que A é a amplitude do movimento vertical do solo, informado em um sismógrafo, A0 é uma amplitude de referência e log representa o logaritmo na base 10.
, em que A é a amplitude do movimento vertical do solo, informado em um sismógrafo, A0 é uma amplitude de referência e log representa o logaritmo na base 10.Disponível em: http://earthquake.usgs.gov.
Acesso em: 28 fev. 2012 (adaptado).A razão entre as amplitudes dos movimentos verticais dos terremotos do Japão e da Argentina é
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre função logarítmica para acertar na hora da prova!
-
Pergunta 10 de 10
10. Pergunta
(UFPR/2017)
Suponha que a quantidade Q de um determinado medicamento no organismo t horas após sua administração possa ser calculada pela fórmula:
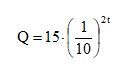
sendo Q medido em miligramas. A expressão que fornece o tempo t em função da quantidade de medicamento Q é:
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre função logarítmica para acertar na hora da prova!

Sobre o(a) autor(a):
Andréia Zanchetti - Os textos e exemplos de apresentação desta aula foram preparados pela professora Andréia Zanchetti para o Blog do Enem. Andréia é formada em Matemática pelo IFRS e possui mestrado pela FURG.
Gostou? Compartilhe!
Continue lendo:
Aqui vão 2 publicações relacionadas que talvez você goste:

Como resolver a prova de Matemática no Enem 2024? Veja as dicas do professor
Por Melina Zanotto | 08 de novembro
Confira as orientações e estratégias do professor Lucas Borguezan para se sair bem na prova de Matemática no Enem 2024.

Aulão Enem de Matemática: revisão intensiva e gratuita para a prova
Por João Vianney dos Valles Santos | 11 de outubro
Assista ao Aulão Enem de Matemática do Curso Enem Gratuito e revise os conteúdos mais importantes para a prova.


