Nesta aula você vai desvendar todos os macetes por trás da construção do gráfico da função polinomial. Preste atenção aos detalhes e arrase na prova do Enem.
Na hora da prova dos vestibulares, um tipo de questão que assusta bastante os alunos são as questões sobre funções polinomiais. Isso porque, dependendo do grau, a resolução costuma ser uma função bem extensa. Na verdade, apenas ao observar o grau do polinômio e o sinal do coeficiente principal você já consegue imaginar como será o comportamento do gráfico. Acompanhe a aula a seguir e acabe com suas dúvidas sobre o gráfico da função polinomial!
Gráficos de funções polinomiais de acordo o grau
Para o estudo do gráfico de uma função polinomial, iniciamos com um questionamento. O que é o comportamento final de uma função? Tomemos como exemplo uma função polinomial de segundo grau, conhecida também como função quadrática.
Exemplo: Gráfico da função x² – 2.
O gráfico desta função possui a forma:
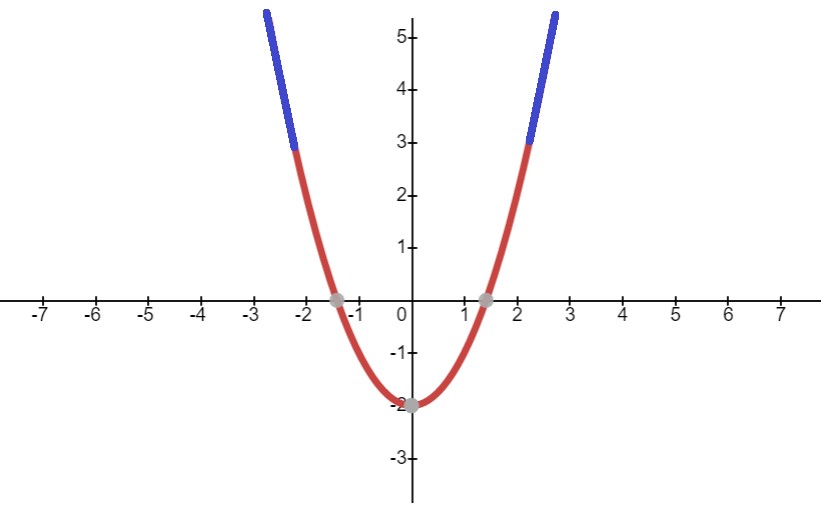
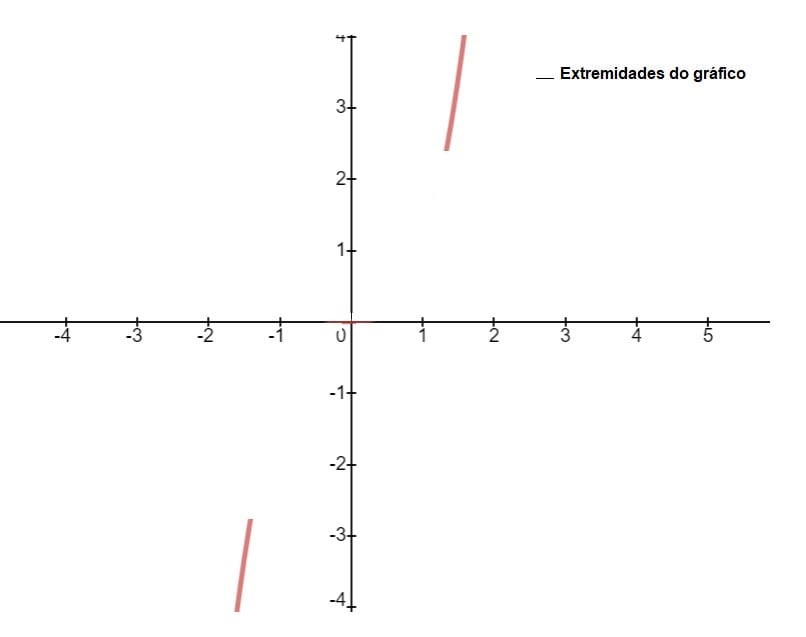
Perceba no gráfico desta função que, conforme tende ao infinito positivo e negativo, as duas extremidades (destacadas em azul) do gráfico da 
tendem ao infinito positivo. Ou seja, este é o comportamento final da função nas extremidades do eixo x. Isso se dá pelo fato de a função quadrática ser de grau par.
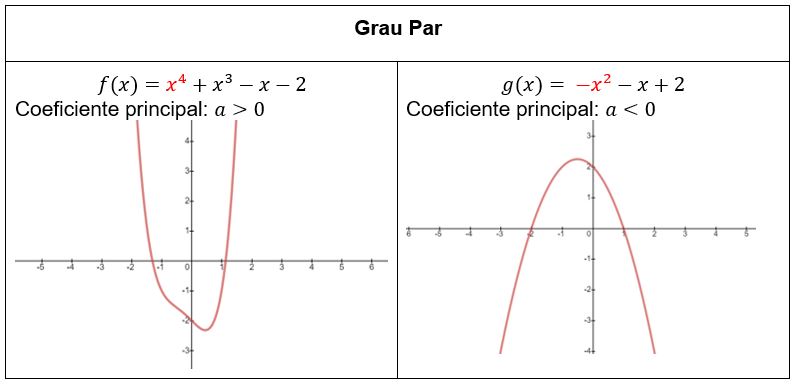
Com isso, temos um dado importante para a análise e construção de gráficos de funções polinomiais. Nelas, o comportamento final do gráfico da função nos dá informações sobre o grau do polinômio. Sendo assim, quando uma função polinomial é de grau par, as duas extremidades do gráfico possuem o mesmo comportamento (as duas extremidades vão para infinito positivo ou infinito negativo). O sinal do coeficiente principal determina se ambas se aproximam do infinito positivo ou do infinito negativo.
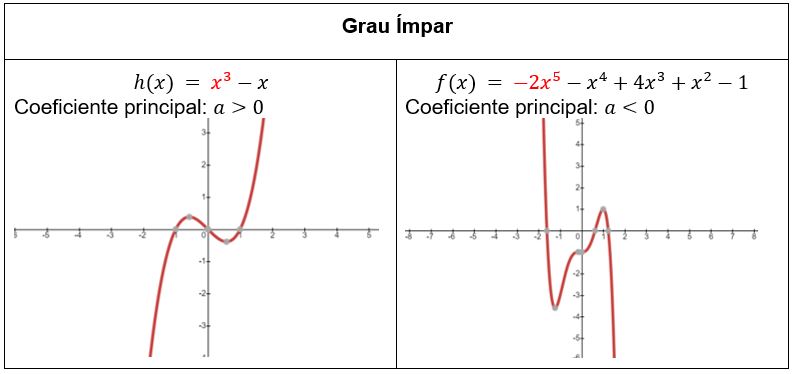
Já quando a função tem grau ímpar, o comportamento da função nas extremidades é o oposto (uma extremidade vai para infinito positivo e outra vai para o infinito negativo). O sinal do coeficiente principal é que determina qual extremidade vai para infinito positivo e qual extremidade vai para infinito negativo.
Analisando funções polinomiais
Agora que você já sabe sobre o comportamento do gráfico da função polinomial segundo seu grau, vamos analisar a função através de suas raízes. Para isso, utilizaremos como exemplo o polinômio
Comportamento final
Para encontrar o comportamento final desta função, podemos reescrevê-la na forma padrão para examinar seu coeficiente principal. Assim:
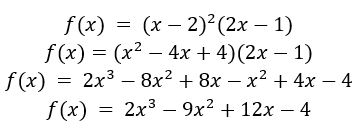
O coeficiente principal do polinômio é 2x³. Portanto, o comportamento final da função será o mesmo comportamento de uma função de grau ímpar e coeficiente positivo (a > 0).
Raízes
Como você já sabe, para encontrar as raízes reais de uma função polinomial, basta resolver a 
, encontrando, assim, os pontos onde o gráfico da função intercepta o eixo X. Resolvendo :
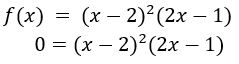
Nesse caso, como o produto entre duas raízes é zero, temos pela propriedade do produto das raízes, que: x – 2 = 0 ou 2x -1 = 0.
Então: x = 2 ou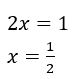 
Assim, as raízes reais do polinômio são os pontos (2, 0) e (1/2, 0).
Importante: funções polinomiais podem ter raízes reais e imaginárias. Quando as raízes são reais, o gráfico intercepta o eixo X naquele ponto, e quando as raízes são imaginárias, o gráfico não intercepta o eixo X.
Multiplicidade de uma raiz
Para compreender o que significa a multiplicidade relacionada à raiz é importante ter em mente as propriedades da fatoração. Por exemplo, no polinômio 
O número 2 é uma raiz de multiplicidade 2. Uma raiz de multiplicidade 2 é chamada de raiz dupla.
Isso é fácil de perceber se você reescrever essa função como:
Observe que, ao expandirmos a função, o fator (x – 2) é escrito duas vezes, então quando você resolver a obterá x = 2 duas vezes.
É importante ter isso em mente porque o comportamento do gráfico é diferente entre raízes de multiplicidade par e raízes de multiplicidade ímpar.
- Se uma função tiver uma raiz de multiplicidade ímpar, o gráfico de
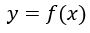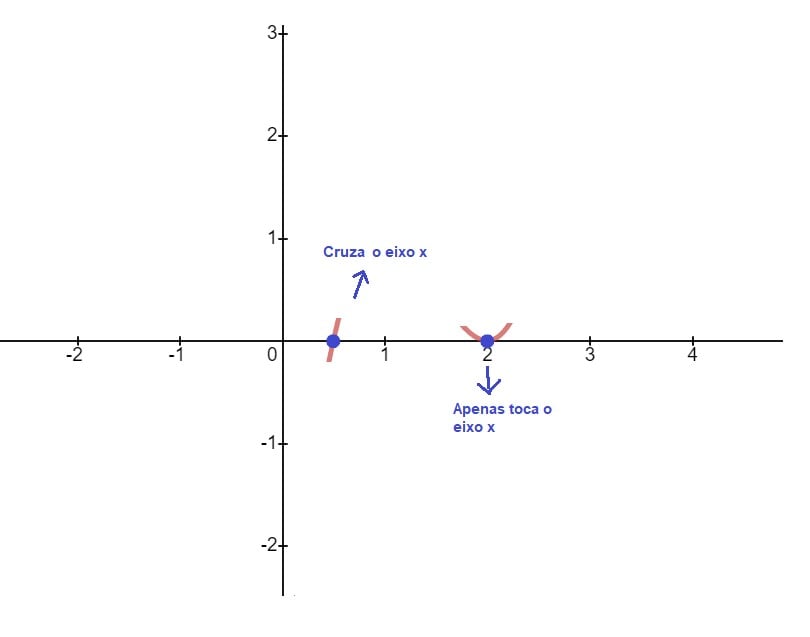
vai cruzar o eixo naquele valor. - Se uma função tiver uma raiz de multiplicidade par, o gráfico de 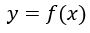vai apenas tocar o eixo naquele ponto.
Então, o gráfico de 
apenas toca o eixo X no ponto (2, 0) e cruza o eixo X no ponto (1/2, 0).
Interceptação no eixo y
Para encontrar onde o gráfico da função polinomial intercepta o eixo Y, basta calcular 
.
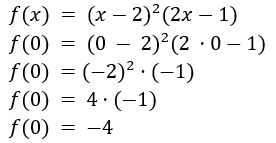
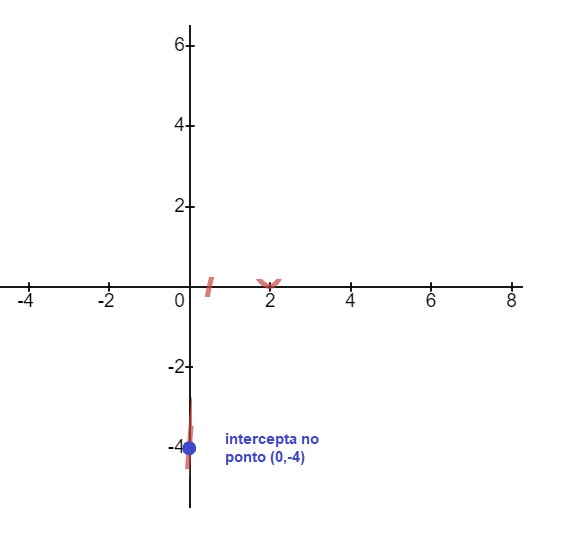
Então o gráfico intercepta o eixo Y no ponto (0, -4):
Plotando o gráfico
Agora, com todas as informações acima, é possível esboçar o gráfico da função polinomial
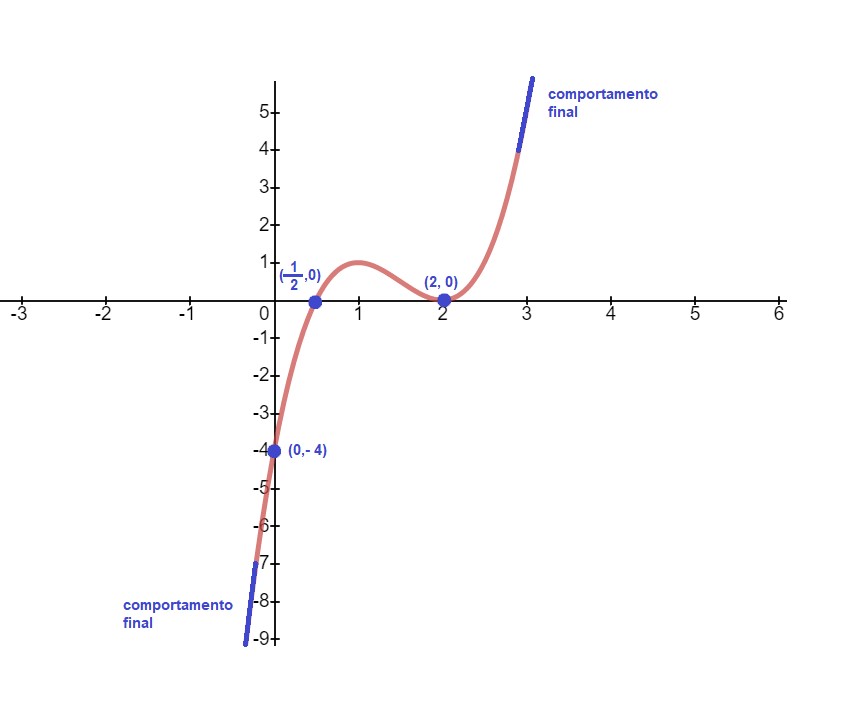
Viu como através do conhecimento de alguns pontos é possível plotar o gráfico?
Videoaula
Exercícios sobre gráfico de função polinomial
Questão 01)
Seja f a função, cujo gráfico é dado a seguir.
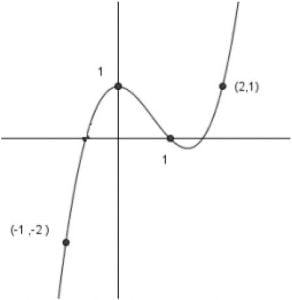
Sabendo que f é polinomial de grau 3, então, o valor da função no ponto x = 3 é igual a
a) 3
b) 5
c) 9
d) 10
e) 27
Questão 02)
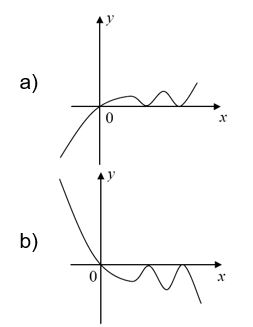
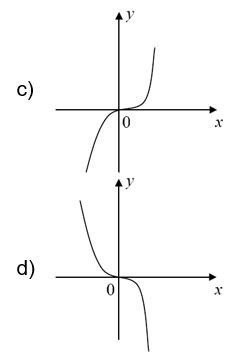
Considere a função polinomial 
, definida por f(x) = –x3 – x. O esboço que melhor representa o gráfico de f é
Questão 03)
A figura abaixo mostra o gráfico do polinômio P(x), de 5º grau e coeficientes reais, que apresenta uma única raiz real.
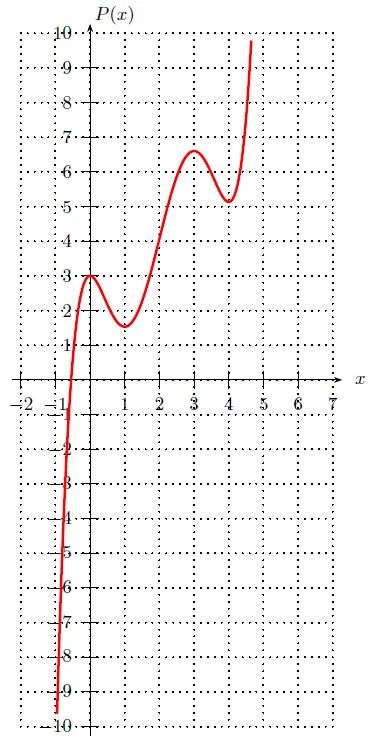
O número de raízes reais do polinômio Q(x), dado, para todo x real, pela expressão Q(x) = 2 – P(x), é igual a
a) 1.
b) 2.
c) 3.
d) 4.
e) 5.
Gabarito:
- D
- D
- C
