Lentes convergentes, divergentes e justapostas

Nesta aula de Física para o Enem, você continuará estudando as características das lentes esféricas. Aqui você irá entender como é feito o cálculo para se colocar lentes nos óculos e verá como as imagens podem ser formadas em lentes convergentes e divergentes. Aprenderá ainda sobre os principais conceitos utilizados na produção de dispositivos ópticos que têm lentes esféricas justapostas e sobre o funcionamento do olho humano. Fique com a gente e aprenda mais! Com certeza você vai mandar bem no Enem e vestibulares!

Uso de lentes esféricas

A fabricação de lentes para equipamentos de uso cotidiano como óculos, binóculos e microscópios deve levar em consideração, entre outros fatores, o material do qual a lente é feita e as curvaturas das faces das lentes. O material escolhido define o índice de refração da lente, e as curvaturas das faces determinam seu perfil. Para a equação dos fabricantes de lentes tudo isso conta. Veja como ela é escrita:

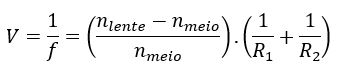
Onde:

V➝ é a vergência da lente;

f ➝ é a distância focal da lente;

n_lente ➝ é o índice de refração do material;

n_meio ➝ é o índice de refração que envolverá a lente;

R₁ e R₂ ➝ são os raios de curvaturas das faces da lente.

É importante lembrar do detalhe de que o foco para lentes divergentes sempre será negativo.

Para entender melhor, vamos ver um exemplo?

Exemplo: Uma lente delgada de vidro, cujo índice de refração é 1,5, é biconvexa, possuindo raios de curvatura iguais a 50 cm. A lente é mergulhada em um líquido de índice de refração igual a 2,0. Determine:

a) A distância focal dela;

b) A vergência da lente.

Resolução:

a) A distância focal pode ser calculada pela fórmula que aprendemos acima, a dos fabricantes de lentes.

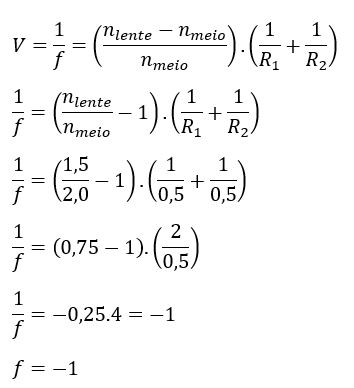
A distância focal é 1 m.

b) A vergência da lente é o oposto da distância focal.

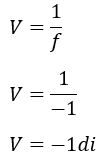
Antes de entrarmos no assunto de formação de imagens pelas lentes convergentes e divergentes, veja a aula sobre espelhos esféricos. A revisão é importante porque na próxima parte desta aula iremos utilizar tanto a equação dos pontos conjugados (Equação de Gauss) como a equação do aumento linear transversal. Então, se você não lembra desse conteúdo, dê uma espiadinha na aula de espelhos esféricos!

Formação de imagens nas lentes convergentes e divergentes

Neste tópico veremos como ocorre a formação de imagens nas lentes convergentes e divergentes, e também como são formadas as imagens resultantes da justaposição de lentes.

Formação de imagens nas lentes convergentes.

Vamos explorar três casos principais para lentes convergentes. As imagens formadas pelas lentes convergentes podem ter características diversas. Essas características dependem da distância do objeto em relação à lente.

1^o Caso: Objeto situado a uma distância da lente maior que 2F₀.

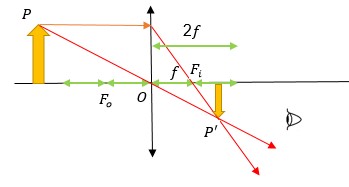
Como você pode observar no esquema, a imagem será real (porque se forma do mesmo lado do observador, representado pelo olho), invertida e menor que o objeto. E sempre estará localizada entre F_i e 2F_i.

Como é real, ela pode ser projetada em um anteparo ou gravada. Esse é o princípio básico do funcionamento de uma máquina fotográfica.

2^o Caso: Objeto situado a uma distância da lente entre F₀ e 2F₀.

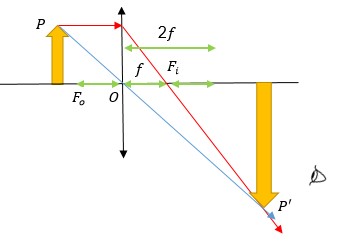
A partir do esquema acima podemos concluir que a imagem será real, invertida e maior que o objeto. Observe que a imagem estará sempre localizada a uma distância maior que 2F_i. Por ser real, pode ser projetada. Esse é o princípio básico do funcionamento dos projetores ou máquinas fotocopiadoras em seleção de cópia ampliada.

3^o Caso: Objeto situado a uma distância da lente menor que F₀ .

 

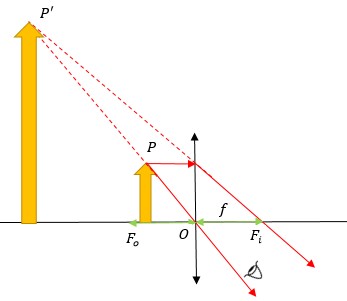
Como você pode observar, nesse caso, diferentemente dos demais, a imagem se forma do mesmo lado da lente que está o objeto observado. Sendo assim, a imagem será virtual, direita e maior que o objeto. Estará sempre localizada atrás do objeto. Esse sistema é a base de funcionamento das lentes de aumento (lupas).

Formação de imagens nas lentes divergentes

Agora veremos imagens decorrentes de lentes divergentes. Elas formam imagens com características iguais, qualquer que seja a distância do objeto a lente.

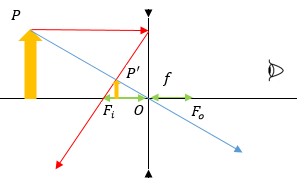
Como você pode observar pelo esquema acima, a imagem sempre será reduzida, virtual e direita. E sempre estará localizada entre F_i e o centro 0. Encontramos esse exemplo em “olhos mágicos” de portas.

Justaposição de lentes

Quando duas lentes delgadas são justapostas, elas passam a funcionar como se fossem uma nova lente cuja vergência total ou vergência equivalente é dada por:

Isso significa que duas lentes justapostas têm suas vergências adicionadas. A vergência total também pode ser escrita como a soma dos inversos de duas distâncias focais:

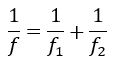
Esse princípio é utilizado na fabricação de instrumentos como o microscópio, aumentando o seu potencial de aumento dos objetos observados.

Para compreendermos melhor, vamos ver um exemplo:

Exemplo: A objetiva de uma filmadora é a associação de duas lentes delgadas justapostas, conforme figura. Uma delas é convexo-côncava, de índice de refração 1,7, e a outra é biconvexa, de índice de refração 1,5 e raios de curvatura iguais a 10 cm. A face livre da lente convexo-côncava tem raio de 20 cm. Determine:

a) A vergência de cada uma das lentes,

b) A vergência da lente equivalente ao sistema.

Resolução:

a) Vamos utilizar a equação dos fabricantes de lentes, mas antes vamos extrair os dados da questão:

Temos que: n_lente =1,7; n_ar =1; R₁ = 20 cm = 0,2 m; R₂ = -10 cm = -0,1 m.

O sinal é negativo devido à face côncava.

Lente convexo-côncava:

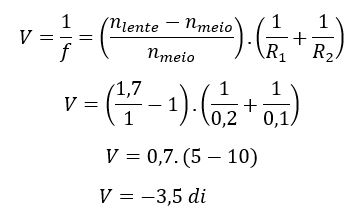
Lente biconvexa:

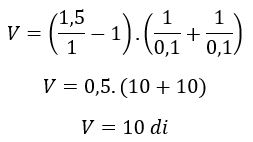
b) A vergência da lente equivalente é a soma das vergências das lentes associadas:

V_total = V₁ + V₂

V_total = -3,5 + 10 = 6,5 di

Videoaula

Você pode rever o conteúdo de lentes convergentes e divergentes assistindo o vídeo no link:

Exercícios sobre lentes convergentes, divergentes e justapostas

1 – (PUC GO/2019)

Em lentes esféricas que apresentam comportamento convergente, os raios de luz que incidem paralelamente entre si sofrem refração e tomam direções que convergem a um único ponto. Considere uma câmara fotográfica que faz uso de uma lente convergente de distância focal 6 cm. Se um objeto real de 30 cm de altura for colocado a 24 cm dessa lente, a posição da imagem será (marque a alternativa correta):

a) 3 cm.

b) 5 cm.

c) 8 cm.

d) 12 cm.

2 – (PUC RS/2018)

O edifício 20 Fenchurch Street, localizado em Londres e conhecido como Walkie Talkie, tem causado diversos problemas para a sua vizinhança. Moradores e funcionários da região têm argumentado que, desde a sua construção, os ventos estão mais intensos nas imediações do prédio. Além disso, houve registros de carros estacionados nas proximidades do prédio que tiveram suas pinturas danificadas e suas peças derretidas por conta da reflexão da luz solar ocasionada pelo arranha-céu.

Os carros foram danificados porque pelo menos uma das faces do prédio tem formato semelhante a

a) um espelho côncavo.

b) um espelho convexo.

c) uma lente divergente.

d) uma lente convergente.

3 – (FAMERP SP/2016)

Na figura, um texto é visto através de duas lentes esféricas, 1 e 2. A imagem formada pela lente 1 aparece menor do que o próprio texto e a imagem formada pela lente 2 aparece maior.

 

Pela observação da figura, constata-se que a lente 1 é __________ e a imagem por ela formada é __________  e que a lente 2 é __________ e a imagem por ela formada é __________.

Assinale a alternativa que preenche, correta e respectivamente, as lacunas apresentadas acima.

a) divergente – real – convergente – real

b) convergente – virtual – convergente – real

c) divergente – virtual – convergente – virtual

d) divergente – virtual – convergente – real

e) convergente – virtual – convergente – virtual

Gabarito:

1. C
2. A
3. C

Compartilhe: