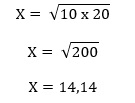Como calcular média aritmética e média ponderada
Confira como calcular uma média aritmética. Saiba que este é um conteúdo essencial para você gabaritar as questões de matemática do Enem e dos vestibulares! Veja nossa aula e teste o que aprendeu com a nossa lista de exercícios!
Um colega seu precisa calcular sua média final para saber se passou de ano ou não. Você saberia ajudá-lo? Para poder ajudar seu amigo, você precisará recorrer aos parâmetros da Estatística para ajudá-lo a resolver seu problema.
Nesta aula de Matemática para o Enem você vai aprender o que é média, quais seus tipos e aplicações em problemas cotidianos. Depois de ver as aulas de revisão e de ler o conteúdo escrito, não se esqueça de resolver os exercícios!
Introdução ao cálculo da Média
Confira agora com o professor Lucas Borguezan, do canal do Curso Enem Gratuito, os fundamentos da estatística para você gabaritar no Enem e nos vestibulares.
Média aritmética
A média aritmética é um parâmetro que permite comparar e entender a distribuição de dados relativos a um fenômeno estatístico.
Exercícios resolvidos
Para entendermos melhor, vejamos alguns exemplos de como isso pode ser cobrado em questões do Enem. Acompanhe os exercícios resolvidos a seguir.
Exemplo 1
Em um time de futebol, as idades dos jogadores titulares são: 25 anos, 27 anos, 22 anos, 30 anos e 31 anos. Qual a idade média dos jogadores do time?
Solução
Para resolver esse problema, vamos somar as idades apresentadas, ou seja,
25+27+22+30+31=135
Feito isso, devemos dividir o resultado obtido pelo número de jogadores titulares, que no caso, são 5.
135/5=27
O número 27 é chamado de média aritmética. Os números 25, 27, 22, 30 e 31 são chamados de variáveis ou números. Assim, podemos escrever que:
A média aritmética de n números (ou fatores) representa a soma de todos os números dividida por n.
Exercícios resolvidos
Veja agora com o professor Sérgio Sarkis exemplos resolvidos com as médias Artimética Simples e Ponderada.
Vamos resolver mais um exemplo para você ficar fera.
Exemplo 2
Paulo recebeu suas notas de Matemática do último bimestre. São elas: 6,0; 7,0 e 5,0. Sabendo que a média bimestral deve ser maior ou igual a 7,0 determine se Paulo ficou ou não recuperação.
Solução
As notas de Paulo são os n números e o total de notas são 3. Calculando a média, obtemos:
M= (6,0+7,0+5,0)/3
M= 18/3
M=6,0
Como podemos notar que a média de Paulo é menor que 7,0, logo ele irá precisar de recuperação.
Vamos supor agora, que o professor de Paulo tenha dado pesos diferentes para cada nota. Para a primeira nota o peso dado foi 2, para a segunda 7 e para a terceira 1.
Será que, agora, com os pesos diferentes, Paulo ainda precisa de recuperação? É o que estudaremos a seguir!
Média ponderada
A média aritmética ponderada de “n” números é a soma dos produtos entre cada número e o seu respectivo peso. Depois, basta fazer a divisão entre o resultado obtido e a soma dos pesos.
Exercícios resolvidos
Exemplo 3
Vamos aplicar essa definição no exemplo do Paulo.
São os números: 6,0; 7,0 e 5,0
São os pesos: 2, 7 e 1.
Calculando a média ponderada, obtemos:
Mp= (6,0 x 2+7,0 x 7+5,0 x 1)/(2+7+1)
Mp= (12+49+5)/9
Mp= 66/9
Mp=7,3
Portanto, Paulo não teria a necessidade de realizar a recuperação, pois 7,3 é maior que a média exigida para passar direto. Bom, agora é o Paulo que ficará responsável de convencer a sua professora a optar pela média aritmética ponderada.
Exemplo 4
Não esqueça que: a média aritmética ponderada depende das regras estabelecidas, dos pesos que você atribui para cada número, para o seu cálculo.
Os pesos atribuídos são chamados de fatores de ponderação, que na verdade é, o quanto você da relevância para determinado número. Analisaremos a seguinte situação:
Suponha que Paulo trocou de escola esse ano. Como Paulo é atleta ele ganhou um desconto na mensalidade de 90%, diferentemente, da escola do ano passado, que oferecia um desconto de 40%. Você saberia dizer qual a média geométrica dos números dados?
Solução
Vamos colocar os números dados em uma tabela, para facilitar a resolução do problema. Para calcularmos, inicialmente devemos determinar o índice.
Para calcularmos, inicialmente devemos determinar o índice.
O índice é a quantidade de fatores analisados, no caso de Paulo, é a quantidade de anos que recebeu o desconto, ou seja, 2. Esse índice representará o índice do radical.
Assim, a média geométrica é calculada pela fórmula: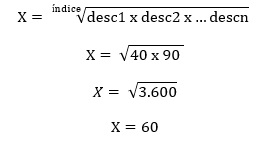
Portanto, a média geométrica é um conjunto de n números positivos é o número positivo, que se obtém, multiplicando os n números dados e extraindo a raiz de índice n deste produto. Utilizamos a média geométrica em situação que há aumentos sucessivos. Tente resolver o próximo exercício, e depois confira a sua resposta.
Exemplo 5
Suponha que você recebeu um aumento de 10% em sua mesada no ano passado e de 20% neste ano. Não seria correto analisar o aumento utilizando média aritmética, pois o aumento de 20% também incidiu sobre o aumento anterior de 10%. Sendo assim, usaremos a média geométrica.
Solução
Fatores: 10% e 20%
Índice: 2 (quantidades de anos)
Calculando a média obtemos:
Concluímos que, receber um aumento de 10% no primeiro e outro de 20% no segundo ano é equivalente a receber dois aumentos de 14%.
Resumo
Viu como é simples? Para se aprofundar, assista ao vídeo a seguir, em que o professor Lucas faz um resumo sobre o tema, com exercícios resolvidos das provas do Encceja:
Exercícios sobre médias
Para terminar, resolva os exercícios sobre média simples e ponderada selecionados pela equipe do Curso Enem Gratuito!
Sumário do Quiz
0 de 10 questões completadas
Perguntas:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
Information
.
Você já fez este questionário anteriormente. Portanto, não pode fazê-lo novamente.
Quiz is loading...
You must sign in or sign up to start the quiz.
Para iniciar este questionário, você precisa terminar, antes, este questionário:
Resultados
0 de 10 perguntas respondidas corretamente
Seu tempo:
Acabou o tempo
Você conseguiu 0 de 0 pontos possíveis (0)
| Pontuação média |
|
| Sua pontuação |
|
Categorias
- Sem categoria 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- Respondido
- Revisão
-
Pergunta 1 de 10
1. Pergunta
(UERJ/2018)
Admitindo um retângulo cujos lados medem a e b, sendo a < b, é possível formar uma sequência ilimitada de retângulos da seguinte forma: a partir do primeiro, cada novo retângulo é construído acrescentando-se um quadrado cujo lado é igual ao maior lado do retângulo anterior, conforme ilustrado a seguir.
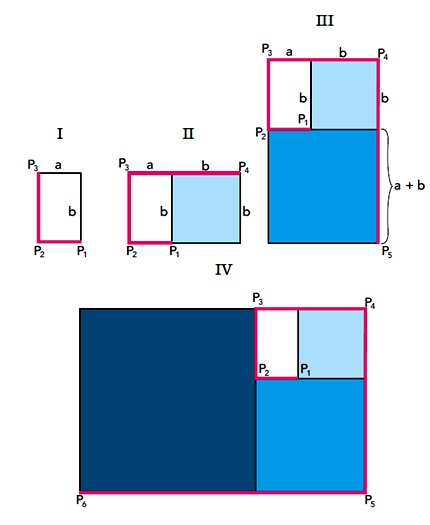
A figura IV destaca a linha poligonal P1P2P3P4P5P6, formada pelos lados dos retângulos, que são os elementos da sequência (a, b, a + b, a + 2b, 2a + 3b).
Mantendo o mesmo padrão de construção, o comprimento da linha poligonal P1P2P3P4P5P6P7, de P1 até o vértice P7, é igual a:
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre média para acertar na hora da prova!
-
Pergunta 2 de 10
2. Pergunta
(Fac. Israelita de C. da Saúde Albert Einstein SP/2018)
Pedro e Luiza estão jogando cartas, sendo que, em cada carta está escrito algum número inteiro e positivo. Cada um inicia o jogo com 5 cartas e informa ao adversário a média dos números de suas cartas. No início do jogo, Pedro avisou que a média de suas cartas era 6 e Luiza avisou que a média de suas cartas era 4. Na primeira rodada Pedro passou uma carta para Luiza e Luiza passou uma carta para Pedro que estava escrito o número 1.
Se a média das cartas que Pedro passou a ter ficou igual a 4,8, o número da carta que Pedro passou para Luiza era
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre média para acertar na hora da prova!
-
Pergunta 3 de 10
3. Pergunta
(PUCCampinas SP/2018)
Quando a dimensão da tela de uma TV é indicada em polegadas, tal valor se refere à medida da diagonal do retângulo que representa a tela. Considere uma TV retangular de 16 polegadas e outra de 21 polegadas. Se as telas das duas TVs são retângulos semelhantes, então, a área da maior tela supera a da menor em, aproximadamente,
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre média para acertar na hora da prova!
-
Pergunta 4 de 10
4. Pergunta
(PUCCampinas SP/2018)

− R está a 1,2 m do chão;
− a altura da cama em relação ao chão é de 40 cm;
− C está a 4 metros de distância da parede em que a TV está fixada;
− a espessura da TV é desprezível.
Nas condições descritas e consultando a tabela, α é igual a
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre média para acertar na hora da prova!
-
Pergunta 5 de 10
5. Pergunta
(UDESC SC/2018)
Em 1958, como trote para os calouros da universidade de Harvard, nos Estados Unidos, um grupo de estudantes precisou medir o comprimento da ponte de Harvard (entre Boston e Cambridge, em Massachusetts), usando como padrão de medida um dos próprios estudantes, um rapaz chamado Oliver R. Smoot. Após horas de medição, com o estudante deitando-se no chão e levantando-se sucessivas vezes para as medidas, concluiu-se que a ponte tinha 364,4 smoots, +/- 1 orelha.
A brincadeira fez tanto sucesso e a medição tornou-se tão popular que, na década de 1980, a ponte foi reformada pela prefeitura, que encomendou blocos de concreto personalizados de 1 smoot de comprimento para a reforma, eternizando as marcações colocadas no solo, que hoje já constam até no sistema de conversão de medidas da ferramenta Google.
Ainda mais interessante é o fato de que, alguns anos após formado, Oliver Smoot tornou-se diretor da ANSI, o Instituto Nacional Americano de Padrões (“American National Standards Institute”) e depois presidente da ISO, a Organização Internacional para Padronização (“International Organization for Standardization”).
Sabendo que Oliver Smoot tinha 5 pés e 7 polegadas de altura na ocasião da medida, desprezando o erro de +/- 1 orelha, e assumindo 1 pé = 30,5 cm e 1 polegada = 2,5 cm, o comprimento da ponte é:
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre média para acertar na hora da prova!
-
Pergunta 6 de 10
6. Pergunta
(ESPM SP/2018)
O terreno mostrado na figura abaixo, cujas medidas estão expressas em metros, foi dividido em dois lotes de mesma área.
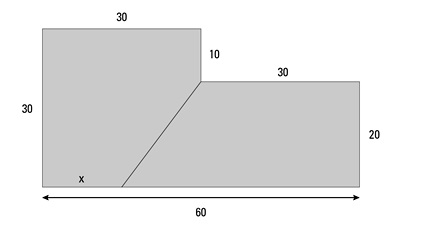
A medida x, em metros, é igual a:
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre média para acertar na hora da prova!
-
Pergunta 7 de 10
7. Pergunta
(ESPM SP/2018)
A gravura mostrada na figura abaixo foi dobrada na linha tracejada MN, a x cm da borda AB.
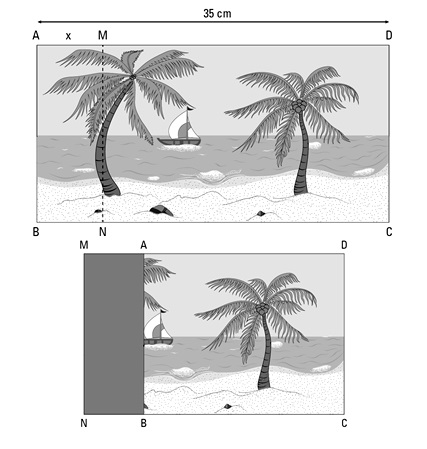
Sabendo-se que, depois da dobradura, a parte oculta da gravura representa 25% da parte visível, podemos afirmar que a medida x é de:
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre média para acertar na hora da prova!
-
Pergunta 8 de 10
8. Pergunta
(UNCISAL/2018)
Em determinado ano, uma prefeitura cobrou de imposto predial R$ 7,00 por metro quadrado de área construída, mais uma taxa fixa de R$ 100,00. Ao mesmo tempo, concedeu um desconto de R$ 48,00 por metro linear do perímetro. Considerando esse mesmo ano e um imóvel térreo, em formato retangular, com os lados proporcionais a 3 e 4, para que o imposto seja o mínimo possível, um dos lados desse imóvel deve medir
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre média para acertar na hora da prova!
-
Pergunta 9 de 10
9. Pergunta
(UNCISAL/2018)
Criado em 1895, o vôlei é um esporte de origem norte-americana e de popularidade significativa em grande parte do mundo. Esse esporte, ao longo do tempo, foi sofrendo alterações tanto nas dimensões de sua quadra quanto em suas regras. A primeira quadra de voleibol tinha 15,24 m de comprimento por 7,62 m de largura. Atualmente, as medidas oficiais são 18 m de comprimento por 9 m de largura. Um aluno deseja representar uma quadra oficial em seu caderno, utilizando uma escala adequada. Para que em seu desenho o comprimento dessa quadra meça 24 cm, a escala deve ser
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre média para acertar na hora da prova!
-
Pergunta 10 de 10
10. Pergunta
(UNCISAL/2018)
O Brasil é conhecido mundialmente como um país com características excelentes para a produção de alimentos, sendo um dos maiores exportadores do mundo, destacando-se na produção de frutas tropicais para conserva in natura, frutas secas, doces e geleias. No Ceará, parte da safra de cana é destinada à fabricação de rapadura. Uma doceira prepara rapaduras em pequenos tabletes e os embala em caixas com 100 unidades cada. Para isso, conta com a ajuda de uma funcionária um pouco distraída ao colocar os tabletes nas caixas. Certo dia, essa doceira resolveu conferir as quantidades de tabletes em um lote de 10 caixas e registrou, em cada uma delas, a respectiva quantidade: 98, 99, 101, 100, 98, 97, 100, 97, 98 e 101. Se X, Y e Z são, respectivamente, a média, a mediana e a moda dessa distribuição, então
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre média para acertar na hora da prova!
Sobre o(a) autor(a):
Cristiane Olska - Os textos e exemplos acima foram elaborados pela professora Cristiane Olska para o Blog do Enem. Cristiane é formada em Licenciatura em Matemática pela Universidade Estadual de Santa Catarina (UDESC), em Joinville. Dá aulas de Matemática em escolas da Grande Florianópolis desde 2016 e elabora módulos de Matemática para empresas do Estado de Santa Catarina e outros.
Gostou? Compartilhe!
Continue lendo:
Aqui vão 2 publicações relacionadas que talvez você goste:

Como resolver a prova de Matemática no Enem 2024? Veja as dicas do professor
Por Melina Zanotto | 08 de novembro
Confira as orientações e estratégias do professor Lucas Borguezan para se sair bem na prova de Matemática no Enem 2024.

Aulão Enem de Matemática: revisão intensiva e gratuita para a prova
Por João Vianney dos Valles Santos | 11 de outubro
Assista ao Aulão Enem de Matemática do Curso Enem Gratuito e revise os conteúdos mais importantes para a prova.