Neste movimento a velocidade varia, e se varia, existe aceleração! Você sabe o que é movimento uniformemente variado, o famoso M.U.V.? Vem revisar este conteúdo!
Aprenda tudo a respeito do movimento uniformemente variado e sua presença em nosso dia a dia. Revise também como você pode representá-lo usando gráficos e como pode obter o deslocamento através do cálculo de áreas. Aprenda ainda como resolver problemas e entender qual fórmula utilizar utilizando alguns macetes.
O movimento uniformemente variado é muito frequente em nosso cotidiano. Neste movimento a velocidade varia, e se varia, existe aceleração!
Para começar esta aula, é muito importante que você entenda que quando um móvel tem sua velocidade aumentada, ocorre aceleração. Já quando a velocidade diminui, ocorre uma desaceleração.
MU x MUV
Concluindo: variou a velocidade, para mais ou para menos, ocorreu aceleração ok?! Veja agora no resumo com o professor Antônio Martins, o Tonho, do canal do Curso Enem Gratuito, um resumo sobre Movimento Uniforme, o MU. Assim você vai perceber as diferenças com o MUV:
Viu só as diferenças básicas? Excelente resumo. Agora, veja o MUV.
Movimento uniformemente variado: M.U.V.
Imagine um ônibus que percorre seu trajeto em certa cidade. Durante seu percurso, ele freia e acelera em diversas situações, como nos pontos de ônibus, nas sinaleiras, aumentando, diminuindo a velocidade e parando às vezes.
Esse é um exemplo onde a velocidade varia, porém não é um movimento uniformemente variado. Ela varia aleatoriamente, sem nenhum padrão. Para ser movimento uniformemente variado, a velocidade tem que variar de maneira uniforme, ou seja, em intervalos de tempos iguais.
Observe a tabela abaixo que descreve o comportamento da velocidade de um móvel em certa rodovia:
| Velocidade(km/h) | 80 | 95 | 110 | 125 | 140 |
| Tempo (h) | 1 | 2 | 3 | 4 | 5 |
Observamos que o móvel tem sua velocidade aumentada em 15 km/h a cada hora que passa. Essa é sua aceleração. Percebe que esse aumento de 15km/h é constante, a cada hora que passa, a velocidade vai aumentando de 15 em 15. Como a velocidade aumenta igualmente em cada intervalo de tempo, podemos dizer que este é um movimento uniformemente variado.
Aceleração
Da mesma forma que a velocidade, existe a aceleração média e a aceleração instantânea. Aceleração média é calculada através da seguinte expressão:
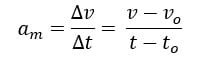Onde: 
Já a aceleração instantânea, representa a aceleração de um corpo em um dado instante, em um tempo muito pequeno. Matematicamente temos:
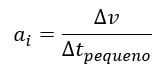
Observe que a aceleração é o resultado da divisão entre a variação de velocidade e a variação de tempo. Sua unidade de medida no SI é m/s2. Vamos ver o porquê de ser essa unidade?
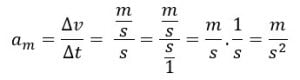
A unidade de aceleração no S.I. é m/s2. Porém, também encontramos a aceleração em km/h2, quando a velocidade estiver sendo medida em km/h.
Se você quiser estudar mais sobre aceleração, assista ao nosso vídeo:
Abordaremos agora algumas das expressões mais importantes do MUV
- FUNÇÃO VELOCIDADE
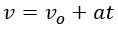(vovô ateu) - FUNÇÃO DA POSIÇÃO
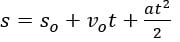(sorvetão) - EQUAÇÃO DE TORRICELLI
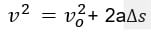(vovô e vovó os dois de asa delta)
Esses macetes podem parecer meio bobos à primeira vista. Porém, podem te ajudar a decorar algumas fórmulas, já que o Enem não apresenta formulários.
Para compreender melhor a aplicação de cada uma, vamos falar detalhá-las:
FUNÇÃO VELOCIDADE (vovô ateu)
Através dessa expressão podemos obter a velocidade final, uma vez conhecido os valores da velocidade inicial (vo), aceleração e tempo observado. Exemplo: Um atleta de corrida dos 100m, desenvolve aceleração constante de 1m/s2 e consegue finalizar em 9,3s. Determine qual o valor da velocidade ao terminar a prova.
Resolução:
Como partiu do repouso, sua velocidade inicial era zero. Temos que a = 1m/s2 e t =9,3s. Vamos substituir os valores na expressão:
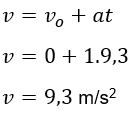
Vamos ver agora como fica no gráfico:
Considere um corpo que se move partindo do repouso com aceleração constante de 5 m/s2. Vamos atribuir valores ao tempo na expressão vovô ateu para calcularmos a velocidade em cada intervalo. A seguir montamos a tabela mais abaixo:
Como partiu do repouso, vo é zero, e a aceleração é 5 m/s2. Então nossa expressão fica apenas v = 5t.
Para t = 0, temos v = 5.0 -> v = 0 m/s
Para t = 1, temos v = 5.1 -> v = 5 m/s
Para t = 2, temos v = 5.2 -> v = 10 m/s
Para t = 3, temos v = 5.3 -> v = 15 m/s
Para t = 4, temos v = 5.4 -> v = 20 m/s
Vamos para tabela:
| Velocidade (m/s) | 0 | 5 | 10 | 15 | 20 |
| Instante (s) | 0 | 1 | 2 | 3 | 4 |
Agora vamos ao gráfico vxt:
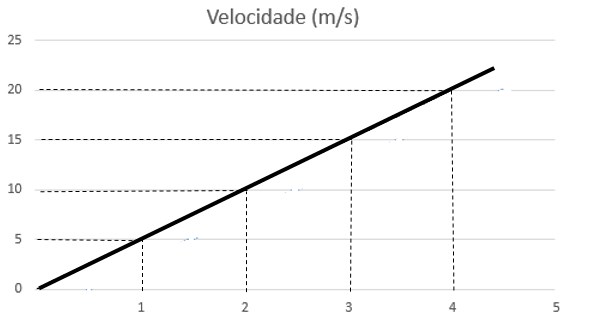
O gráfico da velocidade sempre será uma reta. Nesse exemplo, como a aceleração é positiva, temos a velocidade como uma função crescente. Vamos agora obter o deslocamento realizado através do gráfico?
O deslocamento é igual ao valor da área sob a reta. Por exemplo, qual o deslocamento realizado pelo corpo no intervalo de tempo de 2 a 4 segundos?
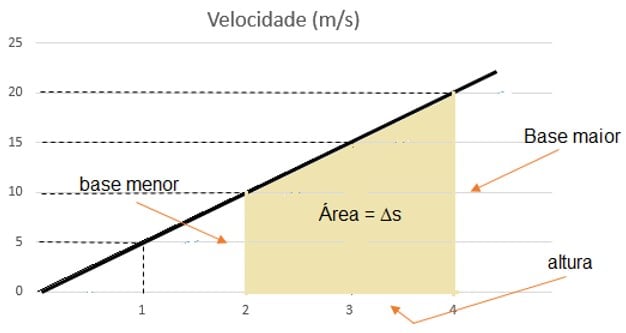
Temos um trapézio cuja área é dada por 
Assim: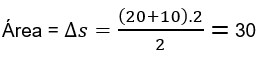 
Então o deslocamento do corpo nos instantes de 2 a 4 segundos foi 30m.
Função Posição
A função velocidade que vimos, permite obter os valores da velocidade de um corpo em um instante qualquer, mas não fornece informação sobre sua localização. Para conseguir essa informação, deduziremos uma nova expressão que nos levará á função posição.
Vimos na função velocidade que o deslocamento nada mais é, que a área sob a reta da função velocidade em função do tempo. Usando as variáveis ao invés dos valores do exemplo, escrevemos:
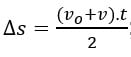; e sabemos que a função velocidade é .
Vamos substituir a equação na equação do deslocamento, temos:
-> essa é a função posição e também a famosa “sorvetão”!
Com essa função podemos obter as posições S de um corpo em qualquer instante t.
Equação de Torricelli
Em muitos casos, o intervalo de tempo não é conhecido. Dispomos apenas de grandezas como velocidade, aceleração e deslocamento. Nessas situações utilizamos a equação de Torricelli, ou vovô e vovó os dois com asa delta.
Da mesma forma que deduzimos a função velocidade, faremos com a Torricelli. Começamos pela função velocidade:
Elevamos ambos os membros ao quadrado:
Agora você sabe de onde saiu a equação de Torricelli!
Classificação dos movimentos uniformemente variados
O movimento pode ser classificado em acelerado, quando a velocidade aumenta ou Retardado, quando a velocidade diminui.
Poderia ser simples assim, mas infelizmente não é! Temos que considerar o sinal da velocidade também.
Então poderemos quatro tipos de movimentos:
- Velocidade positiva e aceleração positiva -> Temos movimento acelerado e progressivo;
- Velocidade positiva e aceleração negativa -> temos movimento retardado e progressivo;
- Velocidade negativa e aceleração positiva -> Temos movimento retardado e retrógrado;
- Velocidade negativa e aceleração negativa -> temos movimento acelerado e retrógrado.
Vamos ver um exemplo:
Um veículo trafega com velocidade constante de 60 km/h e num certo momento desenvolve aceleração constante de 10km/h2. Qual será sua posição após 4 horas acelerando? Primeiro vamos extrair os dados do problema:
Velocidade inicial é 60 km/h; aceleração constante é 10km/h2 e tempo de aceleração 4 horas. Como o problema não informa nada sobre posição inicial, colocamos so = 0. Vamos substituir os valores na função posição:
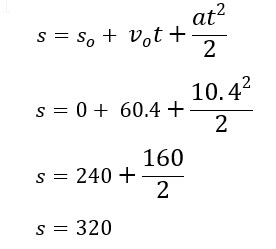
Isso significa que ele estará 320 km a frente.
Salve a imagem abaixo para relembrar as fórmulas de M.U.V.:
Questões sobre movimento uniformemente variado
.
