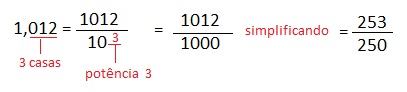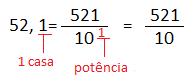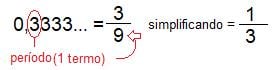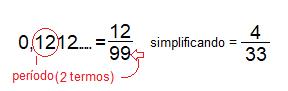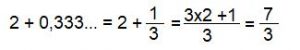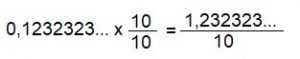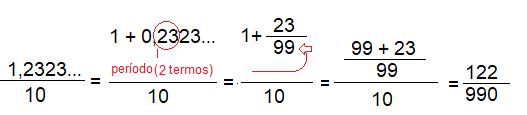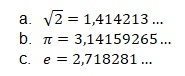Como mudar números da forma decimal para fração
Quer se destacar na prova de matemática do Enem? Tem dificuldade em trabalhar com números decimais? Confere essas dicas e deixe essa preocupação de lado! Aprenda a transformar números decimais em frações!
Que a matemática é tida como um monstro na vida da maioria dos(das) estudantes, principalmente de quem está se preparando para o vestibular e Enem, não é novidade. Mas, a parte divertida e que muitas vezes não é ensinada na sala de aula é a possibilidade de adaptação dos conteúdos. Um bom exemplo são os números decimais: tem estudantes que gostam mais de trabalhar com “números com vírgula” e outros que preferem trabalhar com frações. A mágica acontece quando você percebe que basta transformar números decimais em frações, ou vice e versa, para estudar da forma que você preferir. Vem comigo que eu vou te ensinar!
Antes de começar a aprender como transformar número decimal em fração, é importante ter em mente que nem todos os números decimais se apresentam da mesma forma. Na verdade, existem 3 tipos de números decimais. Vem comigo para conhecer melhor cada um deles!
Primeiro caso: decimais exatos ou decimais finitos
Os números decimais exatos são os que apresentam um número exato de casas decimais (casas depois da vírgula). São os mais fáceis de identificar e também os que mais se apresentam no nosso cotidiano. Veja os exemplos:
- 0, 8
- 0, 5
- 3, 45
- 1, 012
- 52,1
Para transformar os decimais exatos em fração, basta pensar na leitura em voz alta do número. Perceba que quando você lê 0,8 (lê-se oito décimos) fica fácil de imaginar como escrever em fração.
Então, seguindo essa lógica para os exemplos a. e b. temos:
- 0,8 = 8/10 ou ainda “simplificando”, 4/5
- 0,5 = 5/10 ou 1/2
Mas essa lógica não pode ser utilizada com os exemplos seguintes.
É importante lembrar que para toda a transformação de decimais exatos em frações, utilizamos primeiramente um denominador de base 10, fazendo somente depois as simplificações necessárias.
Nesses casos, o que vai determinar a potência do denominador da fração é o número de casas depois da vírgula. Já para o numerador basta “eliminar a vírgula”. Veja o exemplo:
- 3, 45
Temos duas casas depois da vírgula, logo o denominador será dez na potência 2.
Resolvendo os outros exemplos, temos:
- 1, 012
- 52, 1
Bem tranquilo né? Já podemos ir para o próximo caso.
Segundo caso: dízimas periódicas
Chamamos de dízima periódica os números decimais que possuem algum tipo de repetição depois da vírgula. Pode ser a repetição de um ou mais algarismos. Diferente do primeiro caso, as dízimas periódicas são infinitas. Além disso, elas podem ser simples ou compostas, veja os exemplos.
Exemplos.
- 0,33333… (período 3)
- 0,12121… (período 12)
- 2,33333…. (período 3)
- 0,123232323… (período 23, não período 1)
Para efetuar essa transformação, a ideia é parecida do primeiro caso. Mas, aqui vamos utilizar o período como numerador e o denominador da fração será formado pelo número 9. O que vai determinar a quantidade de dígitos 9 é a quantidade de termos do período. Veja os exemplos.
- 0,333333
- 0,121212…
- 2,3333….
Aqui podemos reescrever 2,333… como 2 + 0,33333… Como já sabemos que 0,33333…= 1/3, então:
- 0,123232323…
Uma maneira simples de transformar em fração uma dízima periódica composta, é transformá-la em simples fazendo a seguinte operação:
E então resolvendo normalmente:
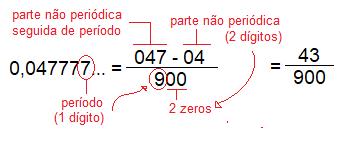
Caso você seja fã de fórmulas, existe uma que podemos utilizar para encurtar esse caminho, onde a fração de uma dízima composta é uma fração onde o numerador é a parte não periódica seguida do período menos a parte não periódica, e o denominador será tantos noves quantos forem os algarismos do período seguidos de tantos zeros quanto forem os algarismos da parte não periódica.
Exemplo:
Terceiro caso: dízimas não periódicas
As dízimas não periódicas são os chamados números irracionais, portanto não são transformadas em frações. São exemplos desses números:
E então? Já está com tudo na ponta da língua? Já está prontíssimo pra entrar na universidade e implorar um décimo pro professor?
Saiba mais sobre o tema na videoaula abaixo:
Exercícios para transformar número decimal em fração
(TJ CE – ESAF). Qual a fração que dá origem à dízima 2,54646… em representação decimal?
a) 2.521 / 990
b) 2.546 / 999
c) 2.546 / 990
d) 2.546 / 900
e) 2.521 / 999
(TRT 15 – FCC). Renato dividiu dois números inteiros positivos em sua calculadora e obteve como resultado a dízima periódica 0,454545… . Se a divisão tivesse sido feita na outra ordem, ou seja, o maior dos dois números dividido pelo menor deles, o resultado obtido por Renato na calculadora teria sido
a) 0,22.
b) 0,222…
c) 2,22.
d) 2,222…
e) 2,2.
Gabaritos: 1)a , 2)e