Como transformar potência de base 10 em número decimal
Você sabia que para medirmos grandezas muito pequenas ou muito grandes podemos usar as potências de dez? Você sabe como passar uma potência de dez para um número decimal? Vem revisar esses conhecimentos de matemática básica com a gente no Curso Enem Gratuito.
Medir é uma técnica importante e devemos dominar essa técnica tanto com aparelhos de medida como compreendê-las numericamente. Um método muito usado para representar medidas é o da representação de números através da potência de base 10.
Nessa aula, você vai aprender o que é uma potência de dez e sua representação. Além disso, aprenderá como transformá-la em um número decimal, aquele número com vírgula que a gente está sempre usando para expressar nosso dinheiro.
E também vamos usar a tabela de prefixos do Sistema Internacional de Unidades para transformar algumas medidas em potência de base dez e também em decimal. Bora revisar?
Onde usamos a potência de base 10
Quando estudamos alguns assuntos da Física, Química, Biologia nos deparamos com alguns números representados com potências de base dez.
A Astronomia nos dá informações com valores muito grandes como a distância entre dois estrela e planetas, como a distância entre o Sol e Netuno que é de aproximadamente 4,5 . 109 Km.
Complicou pra você?
Calma, que professor Sérgio Sarkis, do canal do Curso Enem Gratuito, vai te ajudar. Veja agora:
Nos estudos do átomo recebemos a informação que a massa de um próton é de 1,673.10-27 kg. No átomo temos partículas tão pequenas que não é prático escrever tantos zeros e por isso usamos as potências de 10.
Ou ainda, quando vamos aplicar nosso conhecimentos newtonianos e calcular a força gravitacional usamos a constante gravitacional como 6,67 . 10-11 N.m²/kg².

No círculo amarelo temos um referência ao elétron. E ao átomo. Todos os nomes tem abaixo o tamanho em potências de 10.
Potência de base 10 com expoente positivo
As potências na base 10 com expoentes negativos indicam grandezas muito grandes como a distância da Terra à Lua que tem em média 384.403 quilômetros ou 3, 85. 105 km, esse valor é o que usamos para resolver problemas da Física.
Para complementar seus estudos e ver a aplicabilidade do conteúdo dessa aula, sugiro que você leia um artigo bem curioso como o título: Cientista mostra que a Lua está se afastando da Terra.
Para transformarmos uma potência de base 10 com expoente positivo em um número inteiro basta escrever o algarismo um precedido de tantos zeros indicar o expoente da potência.
Veja a tabela abaixo, com alguns exemplos.

Quando essa potência vem escrita em forma de produto, então escrevemos o número e colocamos tantos zeros quanto indica o expoente da base 10.
Veja o exemplo: 7 x 105 = 700000.
Se o número que antecede a potência de 10 tiver uma vírgula, essa deve ser deslocada para a direita tantas casas decimais indicar o expoente da base 10. Veja o exemplo:
2,3456 x 10³ = 2345,6.
Observe que a vírgula se deslocou três casas decimais.
Aula de reforço: Notação Científica
Veja agora com o professor de matemática Lucas Borguezan um apoio essencial para você dopminar a matéria.
Potência de 10 com expoente negativo
Números acompanhados por potências de dez com expoente negativos indicam medidas muito pequenas. Por exemplo temos a medida da carga do elétron que é de 1,6 . 10 -19 C.
Nesses casos de expoente negativo, contamos para a esquerda o número de casas decimais que indica o expoente. Observe:
235,65 x 10 -4 = 0,023565
Você percebeu que temos que ter quatro casas decimais, não é mesmo? Porém contando para a esquerda a partir da virgula temos somente 3 algarismos, neste caso devemos completar com zeros.
A gente diz que deslocamos a virgula para a frente 4 casas decimais.
Observe a tabela abaixo com mais alguns exemplos:

Agora vamos então fazer um resumo para você de como realizar as conversões de Potências para números inteiros ou decimais.
Regra número 1:
Se o expoente da potência de base 10 for positivo, a vírgula se desloca para a direita.
Vamos mostrar para você alguns exemplos:
a) 23, 42 98 . 10 +3 = 23429, 8
Contamos a partir da virgula 3 casas decimais e deslocamos a vírgula.
b) 0, 000 5 . 10 + 5 = 50
Deslocamos a virgula para a direita 5 casas decimais.
Regra número 2:
Se o expoente da potência de base dez for negativo, a vírgula se desloca para a esquerda.
Vamos exercitar?
a) 23456789 . 10 – 6 =
Primeiro vamos descobrir a virgula. Nos números inteiros a virgula fica escondida. Vamos reescrever esse número:
23456789, 0 . 10 – 6 .
Vamos deslocar a virgula para a esquerda 6 casas decimais: 23456789, 0
A vírgula ficará entre o algarismo 3 e o 4. Então:
23456789 . 10 – 6 = 23, 456789
Fácil, não é mesmo. É só pegar o jeitinho da regra!
Vamos apresentar, a seguir, como usar a tabela de prefixos do SI (Sistema Internacional de Unidades) para converter números com unidades com prefixos em potências de dez e em números decimais.
Sistema internacional de unidades e o uso de prefixos métricos para transformar potencias de dez em números decimais
Um prefixo métrico ou de SI é um nome que fica antes de uma unidade de medida. Esses prefixos são representados por potencias de 10 e indicam múltiplos ou submúltiplos da unidade em questão.
Na tabela 3, temos alguns exemplos desses prefixos e quanto cada um vale em potências de dez.
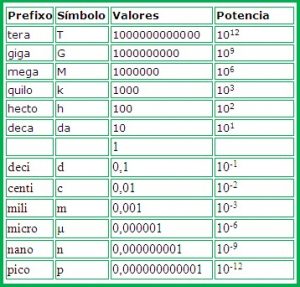
Em estudos da Física, esse prefixos aparecem em unidades de carga elétricas, distância entre cargas, planetas, no cálculo de forças elétricas e gravitacionais em forma de notação científica.
Os prefixos são muito usados para transformar medidas de modo rápido e prático. Veja alguns exemplos:
Transformar as unidades de medidas em metro: 25 cm = 25 . 10 -2 m. Observe que mantivemos o número 25 e substituímos o prefixo c por 10 – 2.
A regra para o uso dos prefixos é essa: multiplique o valor da medida dada por uma potência de dez que corresponde ao prefixo que acompanha a unidade.
Vamos a mais alguns exemplos:
a) 3 mm = 3 . 10 -3 m = 3,0 . 10 -3 = 0, 003 m.
Neste caso, o expoente da base dez é 3 negativo e pela regra deslocamos a virgula três casas decimais para a esquerda. Lembramos que quando um número é inteiro podemos representá-lo na forma decimal: 3 = 3,0.
b) 5 dm = 5 . 10 -1 m = 5,0 . 10 -1 = 0,5 m.
No exemplo acima, o expoente da base dez é 1 negativo e pela regra deslocamos a virgula uma casa decimal para a esquerda. Lembramos que quando um número é inteiro podemos representa-lo na forma decimal: 1 = 1,0.
Resolva os exercícios sobre potência de base 10:
1) A Casa dos Tecidos é da Dona Mariana. Ela vende os tecidos em metros para lojas e alfaiataria. Recebeu essa semana uma nova tabela da fábrica de tecidos com valores reajustados, mas estranhou como os valores estão escritos.
Veja a tabela que Dona Mariana recebeu da fábrica:
| Tecido | Preços em Reais/ metro |
| Seda | 1, 55 . 10 + 2 |
| Algodão | 654,2 . 10 -1 |
| Microfibra | 55555 . 10-3 |
Para ajudar Dona Mariana, sua neta converteu todos os valores em número decimais. A opção correta desses valores apresentados na tabela são respectivamente:
a) R$ 15, 5 ; R$ 65, 42 e R$ 555,5.
b) R$ 155,00; R$ 65,42 e R$ 55555,00.
c) R$ 1550,00; R$ 6,542 e R$ 55, 555.
d) R$ 155,00; R$65,42 e R$ 55, 555.
e) nenhuma das respostas anteriores.
2) O perímetro de um terreno retangular é igual a 0, 065 . 10 3 m.
Esse valor é igual a:
a) 650 m.
b) 6,5 m.
c) 65 m.
d) 0,65 m.
e) 0, 065 m.
3) No Sistema Internacional de Unidades usamos os prefixos para representar potências de base 10. Sabendo que a massa de um ponto material é igual a 0,012546 kg e que k = 10³, então a alternativa que melhor representa a massa desse ponto material é:
a) 0,12546 g.
b) 1,2546 g.
c) 12,546 g.
d) 125,46 g.
e) 1254,6 g.
Gabarito:
1) d 2) c 3) c





