Operações com potência de base dez: aprenda como fazer
A potência de dez é muito usada em várias áreas de conhecimento. Aprenda como resolver operações com potência de base dez para mandar bem nas provas de Matemática e Ciências de Natureza!
Olá, estudante! Tudo bem? Estive comparando as provas do Enem e percebi que o conhecimento das aplicações das potências de base dez (ou potência de dez) é muito importante para a resolução de questões em várias áreas de conhecimento. Por isso, é essencial saber como fazer operações com potência de base dez.
Além de serem necessárias para a resolução de várias questões do Enem, o principal uso das potências de dez é “resumir” números enormes como os trilhões, anos-luz; assim como números muito pequenos, como o tamanho de um elétron e outras partículas atômicas em nosso cotidiano.
As potências de dez nos ajudam a termos noção do tamanho das grandezas que são nos apresentadas pelos estudos científicos.
O que é potência de base dez?
A potência de base dez é uma forma amigável de representar um número com muitas casas decimais ou muito grande.
Veja no resumo com o professor de Matemática Sérgio Sarkis, do canal do Curso Enem Gratuito, uma introdução à Potência de base 10.
A forma mais conhecida do conceito de Potência e apresentada por vários autores é:
![]()
Então uma potência na base dez tem a=10.
Veja os exemplos a seguir:
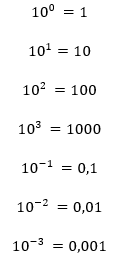
Como você pode perceber nos quatro primeiros exemplos, o expoente positivo indica que se trata da representação de um número inteiro, onde o algarismo 1 tem a seu lado tantos zeros quanto indica o expoente.
Isso quer dizer que se tivermos o número:

Pois 57 é o número de zeros ao lado do um.
Já quanto o expoente da base dez é negativo, como nos últimos três exemplos, indica que temos um número decimal e o expoente indica quantas casas decimais tem esse número.
![]()
Imagina numa prova onde você não pode usar calculadora e ter que multiplicar ou dividir números iguais ou maiores que esse!
Perderíamos muito tempo fazendo os cálculos não é mesmo? E num concurso o tempo deve ser nosso aliado. Por isso agora, vou mostrar a você como usar as operações com potências na base 10.
Operações com potência de base dez
Uma propriedade muito importante que você aprendeu no Ensino Fundamental foi a multiplicação entre potências de mesma base:
![]()
Segundo Lezzi (2005) temos que conservar a base e somar os expoentes (algebricamente, isto é, respeitando a regra de sinais).
Na potência de base 10 não é diferente, veja os exemplos abaixo:
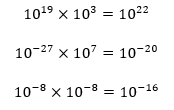
Na divisão de potências de mesma base, aprendemos que devemos repetir a base e diminuir algebricamente os expoentes. Lembro aqui que a fração é uma forma de representar a divisão também.
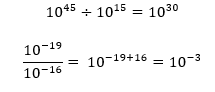
Esse último exemplo é uma forma de alertar a troca do sinal do expoente da potência que se encontra no denominador da fração.
As potências de base 10 não servem somente para expressar números grandes ou pequenos e facilitar cálculos matemáticos. Podemos também transformar unidades sabendo os valores de alguns prefixos. Veja a tabela abaixo:

Com essa tabela em mãos podemos transformar unidades de grandezas como:
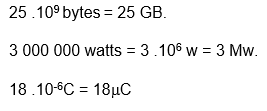
Você entendeu como fazer operações com potência de base dez? Basta trocar a potência de base 10 pelo seu respectivo prefixo e vice-versa!
Notação Científica
Aprenda agora os macetes para gabaritar nas questões de Notação Científica no Enem. Confira com o professor de matemática Lucas Borguezan:
Bibliografia utilizada:
LEZZI, G.; DOLCE, O.; MACHADO, A. Matemática e realidade: 5ª série/ensino fundamental. 5ª edição. São Paulo: Atual, 2005.
INMETRO. Resolução nº 12, de 12 de outubro de 1988. Disponível em: http://goo.gl/RWttO. Acesso em: 08 de jun2018.
Exercícios sobre operações com potência de base dez:
Sumário do Quiz
0 de 10 questões completadas
Perguntas:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
Information
.
Você já fez este questionário anteriormente. Portanto, não pode fazê-lo novamente.
Quiz is loading...
You must sign in or sign up to start the quiz.
Para iniciar este questionário, você precisa terminar, antes, este questionário:
Resultados
0 de 10 perguntas respondidas corretamente
Seu tempo:
Acabou o tempo
Você conseguiu 0 de 0 pontos possíveis (0)
| Pontuação média |
|
| Sua pontuação |
|
Categorias
- Sem categoria 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- Respondido
- Revisão
-
Pergunta 1 de 10
1. Pergunta
(ENEM/ 2017)
Os computadores operam com dados em formato binário (com dois valores possíveis apenas para cada dígito), utilizando potências de 2 para representar quantidades. Assim, tem-se, por exemplo: 1 kB = 210 Bytes, 1 MB = 210 kB e 1 GB = 210 MB, sendo que 210 = 1 024. Nesse caso, tem-se que kB significa quilobyte, MB significa megabyte e GB significa gigabyte. Entretanto, a maioria dos fabricantes de discos rígidos, pendrives ou similares adotam preferencialmente o significado usual desses prefixos, em base 10. Assim, nos produtos desses fabricantes, 1GB = 103 MB = 106 kB = 109Bytes. Como a maioria dos programas de computadores utilizam as unidades baseadas em potências de 2, um disco informado pelo fabricante como sendo de 80 GB aparecerá aos usuários como possuindo, aproximadamente, 75 GB.
Um disco rígido está sendo vendido como possuindo 500 gigabytes, considerando unidades em potências de 10.
Qual dos valores está mais próximo do valor informado por um programa que utilize medidas baseadas em potência de 2?
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre potência de dez para acertar na hora da prova!
-
Pergunta 2 de 10
2. Pergunta
(UERJ/ 2016)
Admita que a ordem de grandeza de uma medida x é uma potência de base 10, com expoente n inteiro, para
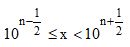 .
.Considere que um terremoto tenha liberado uma energia E, em joules, cujo valor numérico é tal que log10 E = 15,3.
A ordem de grandeza de E, em joules, equivale a:
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre potência de dez para acertar na hora da prova!
-
Pergunta 3 de 10
3. Pergunta
(UNICESUMAR PR/ 2015)
Escrever um número na notação científica significa expressá-lo como o produto de dois números reais x e y, tais que:
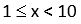 e y é uma potência de 10.
e y é uma potência de 10.Assim, por exemplo, as respectivas expressões dos números 0,0021 e 376,4 na notação científica são 2,1 x 10–3 e 3,764 x 102.
Com base nessas informações, a expressão do número
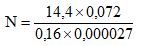 na notação científica é:Correto
na notação científica é:CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre potência de dez para acertar na hora da prova!
-
Pergunta 4 de 10
4. Pergunta
(UFRGS/ 2015)
Por qual potência de 10 deve ser multiplicado o número 10–310–310–310–3 para que esse produto seja igual a 10?
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre potência de dez para acertar na hora da prova!
-
Pergunta 5 de 10
5. Pergunta
(UNIFOR CE/ 2008)
Um número expresso na notação científica é escrito como o produto de dois números reais: um deles, pertencente ao intervalo [1,10[, e o outro, uma potência de 10. Assim, por exemplo, a notação científica do número 0,000714 é 7,14x10–4. De acordo com essa informação, a notação científica do número
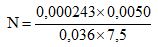 éCorreto
éCorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre potência de dez para acertar na hora da prova!
-
Pergunta 6 de 10
6. Pergunta
(UFGD MS/ 2018)
O valor de 10025 + 1049 – 248 548 é igual a
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre potência de dez para acertar na hora da prova!
-
Pergunta 7 de 10
7. Pergunta
(ENEM/ 2017)
Uma das principais provas de velocidade do atletismo é a prova dos 400 metros rasos. No Campeonato Mundial de Sevilha, em 1999, o atleta Michael Johnson venceu essa prova, com a marca de 43,18 segundos.
Esse tempo, em segundo, escrito em notação científica é
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre potência de dez para acertar na hora da prova!
-
Pergunta 8 de 10
8. Pergunta
(IFMA / 2016)
Sabendo-se que:
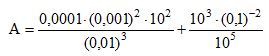 , então o valor de A é:Correto
, então o valor de A é:CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre potência de dez para acertar na hora da prova!
-
Pergunta 9 de 10
9. Pergunta
(Faculdade Santo Agostinho BA/ 2016)
Sendo as células individuais de um organismo muito pequenas para serem vistas a olho nu, é preciso usar microscópios para ampliá-las.
Sabendo-se que um organismo unicelular visto através de um microscópio com campo de visão de 410–4 metros ocupa 1/5 desse campo de visão e que um micrômetro equivale a 10–6 m, é correto afirmar-se que o comprimento, em micrômetros, do organismo é igual a
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre potência de dez para acertar na hora da prova!
-
Pergunta 10 de 10
10. Pergunta
(UNISC RS/ 2015)
As distâncias no espaço são tão grandes que seria muito difícil gerenciar os números se fossem medidas em quilômetros. Então, os astrônomos criaram uma medida padrão, o ano-luz, que é uma medida de comprimento. Ela corresponde ao espaço percorrido pela luz em um ano no vácuo, o que representa, aproximadamente, 9,5 trilhões de quilômetros.
A NASA anunciou recentemente que encontrou o primeiro planeta rochoso com características similares à Terra. Chamado de Kepler-186f, o novo planeta é 10% maior do que a Terra, completa sua órbita em 130 dias e a distância que o separa de nós é de, aproximadamente, 500 anos-luz. Com base nesses dados, é correto afirmar que o número que melhor representa a distância aproximada, em quilômetros, entre a Terra e o Kepler-186f é
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre potência de dez para acertar na hora da prova!

Sobre o(a) autor(a):
Wania Maria de A. Pereira - A professora Wania Maria de A. Pereira é graduada em Física e Matemática pela Universidade Federal de Santa Maria (UFSM) e é Psicopedagoga com enfoque em Gestão de Pessoas (UNC) e especialista em Educação a Distância (SENAC- SC). Atuou na rede particular, estadual e municipal por 26 anos no Estado de Santa Catarina. Autora de diversos materiais didáticos para universidades públicas e privadas na área de Matemática, Metodologia de Ensino de Matemática e Psicopedagogia. Atualmente trabalha na área de Projetos de Tecnologias Digitais de Informação e Comunicação (TDICs). LinkedIn: https://www.linkedin.com/in/wmariaap/.
Gostou? Compartilhe!
Continue lendo:
Aqui vão 2 publicações relacionadas que talvez você goste:

Como resolver a prova de Matemática no Enem 2024? Veja as dicas do professor
Por Melina Zanotto | 08 de novembro
Confira as orientações e estratégias do professor Lucas Borguezan para se sair bem na prova de Matemática no Enem 2024.

Aulão Enem de Matemática: revisão intensiva e gratuita para a prova
Por João Vianney dos Valles Santos | 11 de outubro
Assista ao Aulão Enem de Matemática do Curso Enem Gratuito e revise os conteúdos mais importantes para a prova.


