Probabilidade de união e intersecção de eventos
A probabilidade da união de dois eventos é igual à soma das probabilidades de ocorrência de cada um dos eventos, subtraída da probabilidade da ocorrência dos dois eventos simultaneamente. Entenda como fazer esse cálculo!
Você que está estudando para o Enem já se deparou com diversos conteúdos e muitos deles envolvem conjuntos. Na parte da probabilidade não é tão diferente, afinal, um agrupamento de elementos nada mais é do que um conjunto. Ao determinarmos a possibilidade de ocorrer um evento A ou um evento B, também temos que calcular a probabilidade da união entre esses dois eventos.
Então, mais uma vez, relembramos conceitos dos conjuntos, como união e intersecção. Portanto, nesta aula você vai entender um pouco melhor sobre como são calculadas as probabilidades nesses casos.
Probabilidade da intersecção de dois eventos
Matematicamente falando, a probabilidade da união de dois eventos é igual à soma das probabilidades de ocorrência de cada um dos eventos, subtraída da probabilidade da ocorrência dos dois eventos simultaneamente. O que esse tanto de palavra complicada significa?
Bem, nada melhor do que um bom desenho para exemplificar o que o enunciado acima significa. Sendo assim, sejam dois eventos A e B, dados abaixo pelos círculos vermelho e azul, respectivamente, qual a probabilidade de ocorrer o evento A ou o evento B?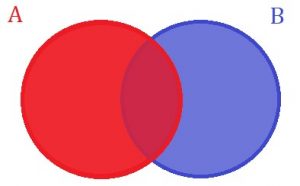
A probabilidade de que ocorra o evento A é representada por toda região em vermelho na imagem, e é dada por P (A).
Já a probabilidade de que ocorra o evento B, é representado na imagem pela região em azul, e é dada por P (B).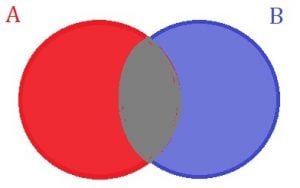
Mas também existe a probabilidade de que ocorra um evento que está na intersecção entre os eventos A e B, representada na imagem pela cor cinza. E como se trata da intersecção entre dois eventos, a probabilidade é dada por P (A ∩ B).
Logo a probabilidade da união de dois eventos pode ser dada pela fórmula matemática:
Onde
Introdução à probabilidade
Veja agora um resumo do canal do Curso Enem Gratuito com uma introdução básica que vai ajudar você a compreender bem esta matéria. Confira com o professor Lucas Borguesan.
Exercício resolvido de probabilidade
Vamos ver um exemplo para entender como essa fórmula funciona na prática?
Exemplo: Em uma caixa existem 15 bolinhas. Elas contêm os números de 1 a 15. Ao retirar uma bola ao acaso, qual a probabilidade de o número ser múltiplo de 3 ou de 5?
A fim de solucionar o exemplo, devemos levar em consideração o espaço amostral S, dado pelo conjunto de todas as bolinhas possíveis, ou seja, S = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15}.
Agora, utilizando a fórmula da probabilidade da união de dois eventos, temos:
(P) A = probabilidade de o número ser múltiplo de 3;
Múltiplos de 3: 3, 6, 9, 12, 15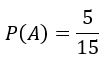
Pois existem 5 múltiplos de 3 em um conjunto de 15 elementos.
(P) B = probabilidade de o número ser múltiplo de 5;
Múltiplos de 5: 5, 10, 15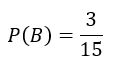
Pois existem 3 múltiplos de 5 em um conjunto de 15 elementos.
P (A ∩ B) = probabilidade de o número ser múltiplo de 3 e 5. Múltiplos de 3 e de 5: 15.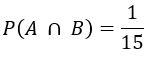
Pois o único múltiplo de 3 e de 5 simultaneamente é o número 15.
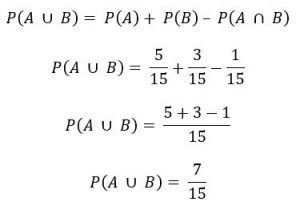
Ou seja, a probabilidade de que a bolinha retirada da caixa tenha um número múltiplo de 3 ou de 5 é de 7/15.
Probabilidade da união de dois eventos
Este foi um exemplo de quando existe a intersecção entre dois conjuntos. Contudo, existem casos em que não ocorre a intersecção. Se não há a possibilidade de dois eventos ocorrerem simultaneamente, então a probabilidade da união de A com B será dada por:
P (A ∪ B) = P(A) + P(B)
Pois
P (A ∪ B) = Ø
Exemplo: Ao lançarmos um dado, qual a probabilidade de sair um número menor do que 2 ou um número par?
Lançamento de dado requer que tenhamos um conjunto dado por S = {1, 2, 3, 4, 5, 6, 7}.
P (A) = número menor do que 2: 1
P (B) =número par: 2, 4, 6
Você percebeu que
(A ∩ B) = Ø
Isso ocorre porque nenhum elemento faz parte de A e de B ao mesmo tempo. Assim:
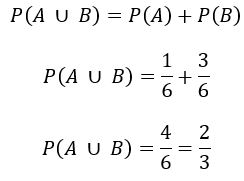
E então? O que achou dessa aula? Mais simples do que parece, não é mesmo?
Exercícios
Questão 1 – (UNCISAL/2018)
Em uma reunião na Secretaria de Saúde de certo município, reuniram-se 28 profissionais da Medicina, (dos quais 18 são mulheres), 27 profissionais da Enfermagem (dos quais 10 são mulheres), e 72 Agentes de Saúde (dos quais 53 são mulheres). Um dos participantes dessa reunião foi sorteado para lavrar a ata da reunião. Sabendo que a pessoa sorteada é mulher, a probabilidade de ela ser médica é igual a
a) 2/9
b) 1/9
c) 2/8
d) 2/8
e) 1/8
Questão 2 – (FAMEMA SP/2018)
Em um curso para profissionais da saúde, há 25 alunos, dos quais 16 são mulheres. Entre as mulheres, 12 têm curso de especialização e, entre os homens, 8 têm curso de especialização. Sorteando-se aleatoriamente dois alunos desse curso, a probabilidade de eles serem de sexos diferentes e pelo menos um deles ter curso de especialização é
a) 4/15
b) 2/5
c) 1/3
d) 3/5
e) 7/15
Questão 3 – (ESPM SP/2018)
Um dado em forma de cubo tem suas faces numeradas de 1 a 6. Outro dado, em forma de octaedro regular, tem suas faces numeradas de 1 a 8. Jogando-se esses dois dados, a probabilidade de que o número obtido no cubo seja maior que o número obtido no octaedro é:
a) 7/12
b) 2/3
c) 5/16
d) 3/4
e) 7/18
GABARITO:
- A
- E
- C
