A regra de três é uma ferramenta matemática simples que ajuda você a resolver problemas complexos, inclusive de geometria.
Aprenda agora a resolver regra de três simples, composta, e também a regra de três inversa. Sempre cai!
Nessa aula você aprenderá noções sobre grandezas diretamente proporcionais e inversamente proporcionais, o que é uma regra de três simples, como usá-la e as aplicações da regra de três composta. Vem com a gente revisar Matemática para mandar bem no Enem!
O que é regra de três
Regra de três é aquela conta “simples”, porém importantíssima e que você com certeza vai achar útil para o resto da vida! Mas, cuidado, porque existem questões para resolver com a “Regra de Três Simples”, que pode ser “Direta”ou “Inversa”, e outros problemas que exigem a “Regra de Três Composta”.
Usamos a “técnica” da regra de três, quando em um conjunto de 2 grandezas, 3 valores são conhecidos e um é desconhecido. Chamamos esse valor desconhecido de incógnita. Sendo assim, a regra serve para descobrirmos o valor da incógnita.
Vale lembrar que o termo grandeza é valido para tudo o que podemos medir de algum modo.
Introdução à Regra de Três
Confira agora com o professor Sérgio Sarkis, do canal do Curso Enem Gratuito:
Tipos de regras de três
Regra de três simples
Esse é o procedimento que utilizamos para resolver problemas de um conjunto de duas grandezas. Essas grandezas podem ser diretamente proporcionais ou inversamente proporcionais.
Para você entender melhor como e quando usá-las, vamos apresentar a Regra de Três Simples através de exemplos. Veja:
A sombra de uma torre mede 4,5 metros e a de uma estaca, colocada verticalmente e no mesmo instante, 90 cm. Calcule a altura da torre, sabendo-se que a vara tem 2 metros de comprimento.
- Resolução:
- Poderíamos resolver o problema apresentado normalmente através da Semelhança de Triângulos.
- Porém, usando a Regra de Três Simples a resolução é mais rápida. Vamos ver como?
- Em primeiro lugar vamos fazer uma tabela e relacionar as grandezas por seu tipo.
- Não esqueça de observar se todas as grandezas estão com a mesma unidade!
No caso desse problema, temos a sombra da estaca em cm então dividimos por 100 e a transformamos em metros: 90 cm = 0,9 m.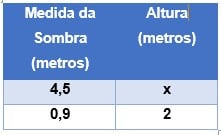
Agora vamos comparar as medidas para descobrir se essas grandezas são diretamente ou inversamente proporcionais
Se aumentarmos a altura da estaca, sua sombra também aumentará, ou se diminuirmos a altura dessa mesma estaca, sua sombra também diminuirá em mesma proporção.
Então concluímos que é uma grandeza diretamente proporcional e nesse caso basta multiplicar as grandezas em Xis: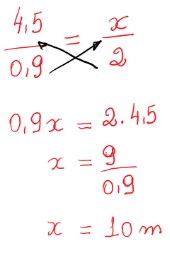
Resposta: A partir da resolução dessa regra de três, podemos concluir que a torre tem 10 metros de altura.
Como resolver Regra de Três
Confira agora com o professor Lucas Borguezan, do canal do Curso Enem Gratuito, as dicas para resolver Regra de Três:
Exercício resolvido de regra de três simples
Exemplo 2
Um trem a 60 km/h demora 2 horas para percorrer uma distância de 120 km.
a) Qual a distância percorrida em 4 horas?
Solução
Se aumentarmos as horas aumentamos a distância percorrida, dizemos que as duas grandezas são diretamente proporcionais. Então basta montar a tabela e relacionar as grandezas: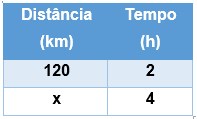
Agora vamos usar a Regra de Três Simples e multiplicar as grandezas em Xis:
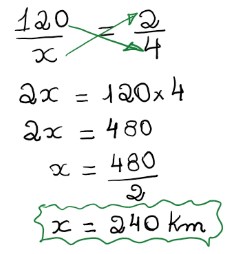Resposta: A distância percorrida pelo trem em 4 horas foi de 240 km.
b) A 90 km/h quanto tempo será necessário para percorrer 120 km?
Solução:
Se aumentarmos a velocidade diminuímos o tempo necessário para percorrermos um distância fixa. Dizemos que as duas grandezas são inversamente proporcionais.
Para resolvermos o problema, basta montarmos as proporções, invertendo a última.
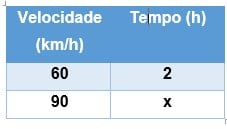Invertendo a última proporção, ficamos com a seguinte relação: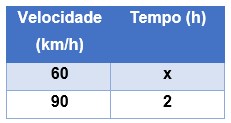
O momento de usar a Regra de Três Simples chegou: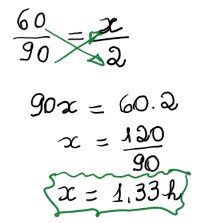
Resposta: O trem percorrerá em 1,33 horas o percurso de 120 km a 90 km/h
Regra de três composta
Regra de três composta é o procedimento para resolver um problema que envolva mais de duas grandezas e uma delas é um valor desconhecido, ou seja, é uma incógnita. A solução para esse caso é aplicação da seguinte propriedade:
“Se uma grandeza é diretamente proporcional a outras duas ou mais grandezas, então será diretamente proporcional ao produto dessas grandezas.”
Caso uma grandeza seja inversamente proporcional, no cálculo sua razão será invertida, tornando-se diretamente proporcional.
Exercício resolvido de regra de três composta
(ENEM) Uma escola lançou uma campanha para seus alunos arrecadarem, durante 30 dias, alimentos não perecíveis para doar a uma comunidade carente da região. Vinte alunos aceitaram a tarefa e nos primeiros 10 dias trabalharam 3 horas diárias, arrecadando 12 kg de alimentos por dia.
Animados com os resultados, 30 novos alunos somaram-se ao grupo, e passaram a trabalhar 4 horas por dia nos dias seguintes até o término da campanha. Admitindo-se que o ritmo de coleta tenha se mantido constante, a quantidade de alimentos arrecadados ao final do prazo estipulado seria de:
- A) 920kg
- B) 800kg
- C) 720kg
- D) 600kg
- E) 570kg
Solução:
O que podemos tirar do enunciado do problema:
Nos 10 primeiros dias foram arrecadados (12kg x 10) = 120kg de alimentos.
Nos 20 dias restantes haverá 50 alunos trabalhando 4 horas por dia.
Identificamos as grandezas envolvidas no problema: nº de alunos, horas/dia, dias trabalhados, Kg arrecadados.
Vamos construir a tabela: Organizamos as grandezas em colunas e usamos a letra x para identificar o termo a ser calculado.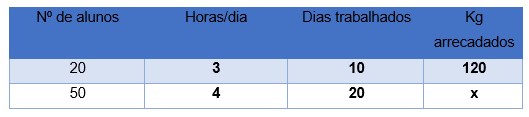
Vamos analisar as grandezas por coluna:
1ª coluna: Se tivermos mais alunos trabalhando, teremos mais arrecadação, então essas grandezas são diretamente proporcionais.
2ª coluna: Se os alunos trabalharem mais horas por dia, teremos mais arrecadação. Então temos grandezas diretamente proporcionais.
3ª coluna: Se tivermos mais dias trabalhados, teremos maior arrecadação. São grandezas diretamente proporcionais.
- Usando a propriedade:
- Se uma grandeza é diretamente proporcional a outras duas ou mais grandezas, então será diretamente proporcional ao produto dessas grandezas.
- Temos:
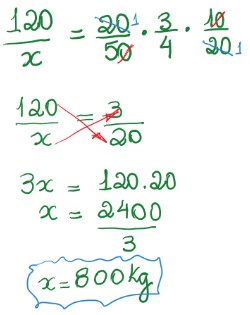Como você pode perceber, simplificamos os valores das frações antes de multiplicar. Isso facilita quando temos cálculos grandes.
Então o total arrecadado nos dois períodos foi de (120kg + 800kg) = 920kg.
Resposta: Alternativa A.
Exercício de regra de três composta
Se 10 carros consomem em 6 dias a quantidade de 1000 litros de gasolina, quantos carros usaremos para consumir somente 500 litros de gasolina no espaço de 2 dias?
- Solução:
- Identificamos as grandezas envolvidas no problema: nº de carros, nº de dias e litros de gasolina.
- Vamos construir a tabela: Organizamos as grandezas em colunas e usamos a letra x para identificar o termo a ser calculado.
Analisamos as grandezas listadas por coluna:
1ª coluna: Número de carros: coluna com incógnita.
2ª coluna: Consumindo a mesma quantidade de gasolina em menos dias indica que usaremos mais carros. São grandezas inversamente proporcional. Nesse caso temos que inverter as grandezas quando usarmos a regra de três.
3ª coluna: Se consumirmos menos gasolina indica que usaremos menos. Grandezas diretamente proporcional.
- Usando a propriedade:
- Se uma grandeza é diretamente proporcional a outras duas ou mais grandezas, então será diretamente proporcional ao produto dessas grandezas.
- Temos
Resposta: Então, usaremos 10 carros para consumir somente 500 litros de gasolina em 2 dias.
Nesta aula você aprendeu que duas grandezas são diretamente proporcionais quando aumentando uma delas, a outra aumenta em mesma proporção ou quando diminuindo uma delas, a outra diminui na mesma proporção;
Também vimos que duas grandezas são inversamente proporcionais quando, aumentando uma delas, a outra diminui na mesma proporção ou quando, diminuindo uma delas, a outra aumenta na mesma proporção;
Você aprendeu ainda que a regra de três simples compara duas grandezas e a regra de três composta compara três ou mais grandezas.
Não esqueça de organizar a tabela com grandezas do mesmo tipo que é fundamental para organizar a resolução dos problemas na regra de três composta.
Resumo em vídeo sobre regra de três Inversa
Referências
BELLO, Pedro. Matemática Básica para Concurso, v1. RJ: Ed. Ferreira, 2006.
MORAES, J. L. de. Matemática e Lógica para Concursos. São Paulo: Saraiva, 2013.
Exercícios sobre regra de três
.
