Tales de Mileto mediu a altura de uma pirâmide com base no comprimento de sua sombra. Descubra como nessa revisão sobre Semelhança entre Triângulos! Ao final, resolva os exercícios para testar seus conhecimentos!
A História da Matemática mostra que por volta de 2500 a.C. os povos não tinham a tecnologia que temos para construir obras faraônicas como as Pirâmides.
Imagine como as pessoas mediam as distâncias que precisavam percorrer entre cidades, o tempo que tinham para cumprir uma meta, ou medir a altura de montes, construções entre outras necessidades. Conseguiu?
Para resolver esse problema, Tales de Mileto achou uma estratégia lógico-matemática para medir a altura de uma pirâmide usou a comparação, percebendo a semelhança entre formas desenhadas pelas sombras. Saiba mais sobre a semelhança entre triângulos e o Teorema de Tales nesta aula de Matemática para o Enem.
A Semelhança entre Triângulos e o Teorema de Tales
O Teorema de Tales aplica o conceito de proporcionalidade entre segmentos de retas paralelas e perpendiculares. Já a semelhança entre triângulos aplica a proporcionalidade para estimar medidas, então aqui o ponto comum entre os dois temas é a proporção.
Mas, quem foi Tales? Tales foi um filósofo, matemático, engenheiro, astrônomo da Grécia Antiga. Nasceu na cidade de Mileto, e por isso ficou conhecido como Tales de Mileto.
Além de elaborar o Teorema de Tales, que é considerado o mais importante nos estudos de Geometria, também foi o primeiro matemático a explicar o eclipse solar.

Como sabemos existem várias aplicações para esse Teorema, porém existe uma histórica que diz que Tales mediu uma pirâmide comparando a medida de sua sombra com a sombra de uma estaca, na qual ele sabia a altura exata.
Como você faria para calcular a altura da pirâmide apenas com uma estaca?

Tales de Mileto percebeu que os raios do sol incidem paralelamente, como feixe de retas paralelas, fazendo assim com que as sombras dos objetos sejam proporcionais a sua altura.
Então, para descobrir a altura da pirâmide, Tales fincou uma estaca na areia, mediu as sombras da pirâmide e depois da estaca em uma determinada hora do dia e estabeleceu uma proporção:
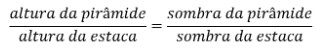
Sendo assim, a partir desse experimentou Tales enunciou seu Teorema:
“Um feixe de retas paralelas determina segmentos proporcionais em duas retas transversais quaisquer.”
O “matematiquês” complicou? Vamos traduzir essa frase para você:
Um conjunto de retas paralelas forma em duas retas transversais ( retas que cortam as paralelas) pedaços menores e proporcionais dessas retas (segmentos).
Com isso, quero que você entenda que:
- Retas paralelas são aquelas que estão separadas por uma mesma distância e nunca se tocam.
- Retas transversais: são retas que cortam outras retas formando ângulos e segmentos de retas.
- Segmentos de retas: são pedacinhos de uma reta.
Aplicação do Teorema de Tales:
Considere a figura abaixo e considere que AB = 4cm, DB = 6 cm, AE = 12 cm e EC = x.
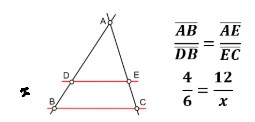
Multiplicamos os meios pelos os extremos, isto é:
![]()
Para obtermos o valor de x precisamos multiplicar e dividir:
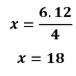
Então o valor do segmento ![]()
O Teorema de Tales e a Semelhança de Triângulos:
Como vimos, a comparação entre triângulos foi a solução para que Tales descobrisse a altura da pirâmide.
Para que os triângulos sejam semelhantes devem obedecer a seguinte condição de semelhança:
“Dois triângulos serão considerados semelhantes se, e somente se, possuírem os três ângulos ordenadamente congruentes e os três lados homólogos e proporcionais.”
O que isso quer dizer? Se tivermos dois triângulos e formos compará-los, para que sejam semelhantes temos que observar se:
a) se seus três ângulos correspondentes têm mesma medida.
b) seus três lados devem ser parecidos e proporcionais.
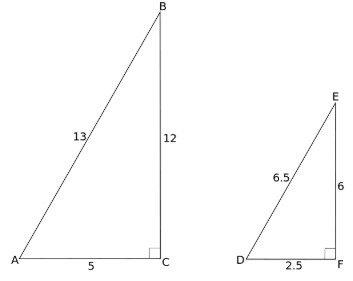
Veja a imagem abaixo:
 Fonte: Wikibooks < https://goo.gl/TMCvdF>
Fonte: Wikibooks < https://goo.gl/TMCvdF>
Esses dois triângulos são semelhantes? Sim, pois os lados AB e DE são homólogos e proporcionais aos outros lados BC e EF, AC e DF.
Se calcularmos as razões entre os lados AB e DE temos:
![]()
Se calcularmos as razões entre BC e EF, temos:
![]()
A razão entre AC e DF é:
![]()
Você já deve ter percebido que as razões entre os lados correspondentes dos triângulos deram o mesmo valor, não é mesmo? Isso ocorre porque os lados são proporcionais.
E quanto aos ângulos? Com certeza são iguais (congruentes).
Com isso podemos concluir que para dois triângulos semelhantes a razão entre seus lados correspondentes sempre será igual a uma constante de proporcionalidade.
Veja a aula do prof. Sarkis sobre a Semelhança entre Triângulos:
Teorema Fundamental da Semelhança
O Teorema Fundamental da Semelhança usa o Teorema de Tales para o cálculo de segmentos de um mesmo triângulo cortado por uma reta paralela e diz que:
“Toda a reta paralela a um lado de um triângulo e que corta os outros dois lados em pontos diferentes vai formar outro triângulo semelhante ao primeiro.”
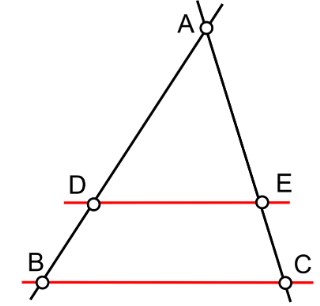
Vamos analisar o triângulo ABC:
 Fonte: Wikimedia < https://goo.gl/7E1Y4K>
Fonte: Wikimedia < https://goo.gl/7E1Y4K>
Nosso triângulo inicial era o ABC, a reta paralela que corta o triângulo é a DE e com isso forma outro triângulo semelhante ao primeiro que é o ADE.
Se a reta r é paralela à BC, então:
a) Os lados AB e AD são proporcionais.
b) Os lados AC e AE são proporcionais.
c) Os lados BC e DE são proporcionais.
E a constante de proporcionalidade deve ser a mesma.
A semelhança de triângulos e o Teorema de Tales deram origem as relações métricas e trigonométricas entre triângulos retângulos. Esse conhecimento ainda será aplicado a outras áreas da Geometria como na Geometria Espacial e Estudo de Quadriláteros e na Física no estudo da Estática de corpos Rígidos.
Exercícios sobre semelhança entre triângulos:
.

