A racionalização dos denominadores nada mais é do transformar um denominador irracional em um número racional. Essa mudança ocorre sem alteração do valor da fração.
Para você que é um amante da filosofia, racionalização provavelmente te lembra o pensamento livre de sentimento ou mitologias. Mas racionalizar não é somente pensar de forma esclarecida e organizada. Na verdade, temos aqui uma só palavra com muitos significados, como na racionalização de denominadores.
Na matemática, racionalizar significa transformar um denominador que antes era um número irracional em um número racional. Veja que, se pararmos pra pensar, é possível fazer uma ligação entre a filosofia e a matemática.
Se ao final dessa aula concluirmos que racionalizar um número torna o restante do cálculo muito mais fácil, então ao racionalizar este número agimos de forma racional e inteligente. Vamos agora ver na prática como isso funciona?
O que é a Racionalização
Veja agora com o professor Lucas Borgueza, do canal do Curso Enem Gratuito.
A racionalização de um número fracionário consiste, basicamente, em se obter uma fração onde o denominador é um número racional e não um número irracional, que geralmente se apresenta em forma de raiz. Qual o objetivo de se fazer essa transformação?
É importante frisar que o número fracionário, depois de racionalizado, permanece com o mesmo valor anterior. O que muda é somente a apresentação dele. Esse melhoramento é uma convenção dentro da matemática, pois todos concordam que ter um número racional no denominador facilita muito na hora de efetuar cálculos.
Nesta aula, iremos aprofundar nossos estudos em três casos de racionalização de denominadores. Preste bastante atenção, pois é fundamental compreender as semelhanças e principalmente as diferenças entre cada um dos casos.
Importante: para este estudo é imprescindível lembrar da propriedade que nos diz que: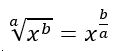 
Primeiro caso de racionalização de denominadores: raiz quadrada
A principal maneira como se apresenta uma raiz quadrada é na forma
. Aqui nesta aula, vamos substituir a letra “a” por um numeral, para facilitar o estudo a partir de um exemplo. Então, tomemos como exemplo a raiz quadrada de 7: 
Para eliminar uma raiz quadrada, basta multiplicá-la por ela mesma. Nesse caso, o cálculo seria:
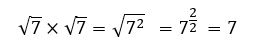
Claro que este é só um exemplo aleatório, pois o cálculo feito acima alterou o valor do número inicial, já que raiz quadrada de 7 é diferente do número 7.
Porém, se nos depararmos com uma fração da forma 
, nosso objetivo primeiro será eliminar a raiz do denominador. Fazemos isso utilizando o mesmo método utilizado acima. Mas, agora, iremos multiplicar não somente o denominador, mas também o numerador por uma raiz quadrada idêntica à que está no denominador.
Temos: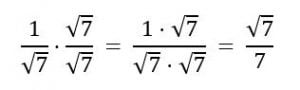 
Mas o que significa multiplicar por 
? Você já deve saber que uma fração representa uma divisão, e um número dividido por ele mesmo equivale a 1, certo? Nesse caso não é diferente, será um elemento neutro na multiplicação, pois equivale a 1.
Chamamos o de fator racionalizante da fração.
Exemplo:
Racionalizar o número: 
.
Nesse caso, o fator racionalizante é o 
. Então, basta multiplicarmos o número por 
:
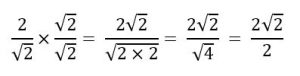
Nesse exemplo, podemos simplificar ainda mais o resultado final, pois se trata de uma multiplicação no numerador, considerando que 
é igual a 1. Temos:
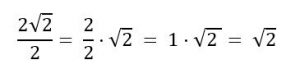
Tendo tudo isso levado em consideração, podemos agora estudar os outros casos de racionalização de denominadores.
Segundo caso de racionalização: raiz não quadrada
A raiz quadrada do primeiro caso de racionalização é a mais comum de ser vista em vários estudos matemáticos, principalmente na parte de trigonometria.
Mas o índice da raiz pode ser qualquer outro, de forma que não teremos mais uma raiz quadrada. Será que o fator racionalizante nesses casos continua sendo igual ao denominador? Vamos descobrir juntos!
Tomemos como exemplo a seguinte fração: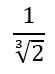 
.
Usando a ideia do primeiro caso, e multiplicando por 
, teremos:
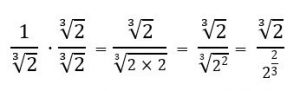
Perceba que, após esse cálculo todo, não conseguimos eliminar o radical. Ou seja, a escolha do fator racionalizante não foi boa. Queremos escolher um fator que, ao final das contas, nos dê um expoente inteiro para o denominador.
Preste atenção no denominador 
, se tivéssemos escolhido um número, onde, no fim das contas ficássemos com o um denominador 
, teria sido ideal pois = 2.
Então, devemos multiplicar o radical por um outro fator, chamado fator de sorte, que nos faça chegar a e não a . Qual é esse fator?
Para isso, utilizamos a regra que nos diz que para um denominador da forma 
, utilizamos um fator racionalizante na forma 
.
Usando essa regra no exemplo anterior, temos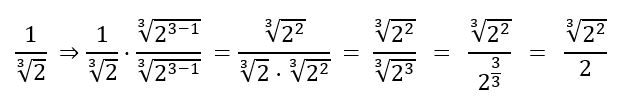
Acredite ou não,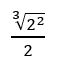 
é a forma mais simplificada de 
.
O terceiro caso é importantíssimo para o estudo de Integrais e Derivadas. Dessa forma, vamos agora a uma explicação detalhada.
Terceiro caso de racionalização: denominador como soma ou diferença
Já dizia o velho ditado, nem tudo são flores, e na matemática não ia ser diferente, não é mesmo? Se uma raiz aparecendo no denominador incomoda, imagina só uma soma de raízes, ou ainda, uma subtração de raízes.
Nestes casos, já te aviso que não basta somente multiplicar por um fator racionalizante igualzinho ao denominador, hein! É preciso relembrar conceitos além da radiciação. Portanto, precisamos relembrar dos produtos notáveis.
Veja a fração abaixo: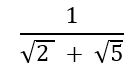
Você deve ter percebido que o denominador dessa fração é uma soma de dois quadrados, e o produto notável que mais se encaixa na resolução deste problema é o produto da soma pela diferença. Esse produto notável nos traz uma regra que diz que (a + b) . (a – b) = a² – b².
Aplicando essa regra na fração, substituindo a e b por valores numéricos, temos que: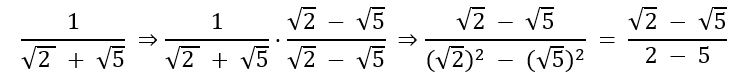
Perceba que no denominador tínhamos uma soma 
, e o nosso fator racionalizante foi uma diferença 
. A grosso modo, podemos dizer que somente trocamos o sinal, o mesmo pode ser feito se tivermos uma diferença no denominador, por exemplo: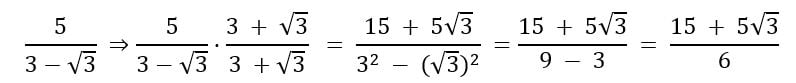
Atenção: perceba que nesse caso, não podemos simplificar o denominador 6 por nenhum dos numerais do numerador, pois se trata de uma soma.
Resumo de racionalização de denominadores
Por fim, chegou a hora de praticar! Vamos aos exercícios?
Exercícios
Questão 01) Usando a tecnologia de uma calculadora pode-se calcular a divisão de 2 por 
e obter um resultado igual a
a) 
b) 
c) 
d) 
e) 
Gab: D
Questão 02) Assinale o que for correto:
01. 
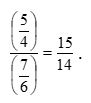
02. 
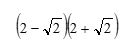é um número inteiro.
04. 
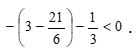
08. 3–2 – 2–3 = –(3–2)(2–3).
16. 
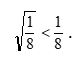
Gab: 11
Questão 03) Eles sabem que racionalizar é assunto do nono ano e não cai com frequência em provas, mas resolvem por via das dúvidas treinarem um pouco. E uma das questões que eles resolveram e acertaram é:
A fração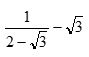 
é igual a.
Qual é a alternativa que eles marcaram?
a) 0
b) 1
c) 2
d) 3
e) 
Gab: C
